(archived) University Physics Notes

University Physics is essentially calculus, but with more careful selection of differential variables.

Chapter 5

Electric Field Intensity (Field Strength)

Electric Field Strength Calculation (Discrete Case)

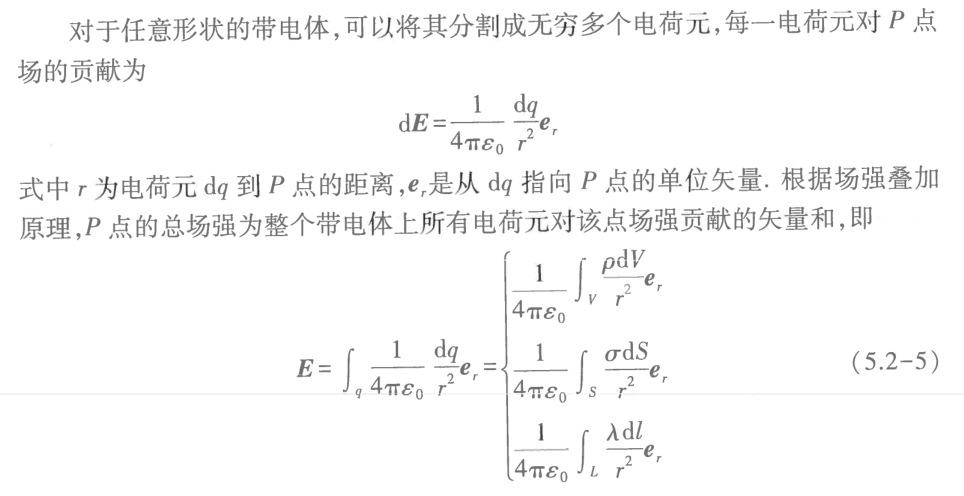
Electric Field Intensity (Continuous Distribution)

Common Electric Field Intensities

Point Charge, Charged Spherical Shell, Charged Sphere (External)

Here, $\overrightarrow{e_r}$ is the unit vector from $q$ pointing to point $P$.

Infinitely long uniformly charged straight line (or very close to the straight line), half-infinite length multiplied by 1/2

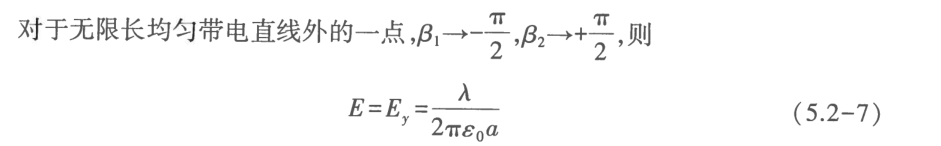
Infinitely Large Uniformly Charged Plane (or at a Distance Very Close to the Plane)

Hemispherical Shell

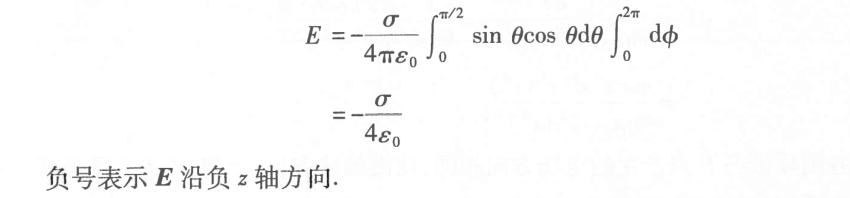
Gauss's Theorem for Calculating Electric Field Strength (Symmetry)

Charged Spherical Shell

To calculate the electric field outside the spherical shell, the shell can be treated as a point charge with all its charge concentrated at the center.

Infinitely Long Cylindrical Surface

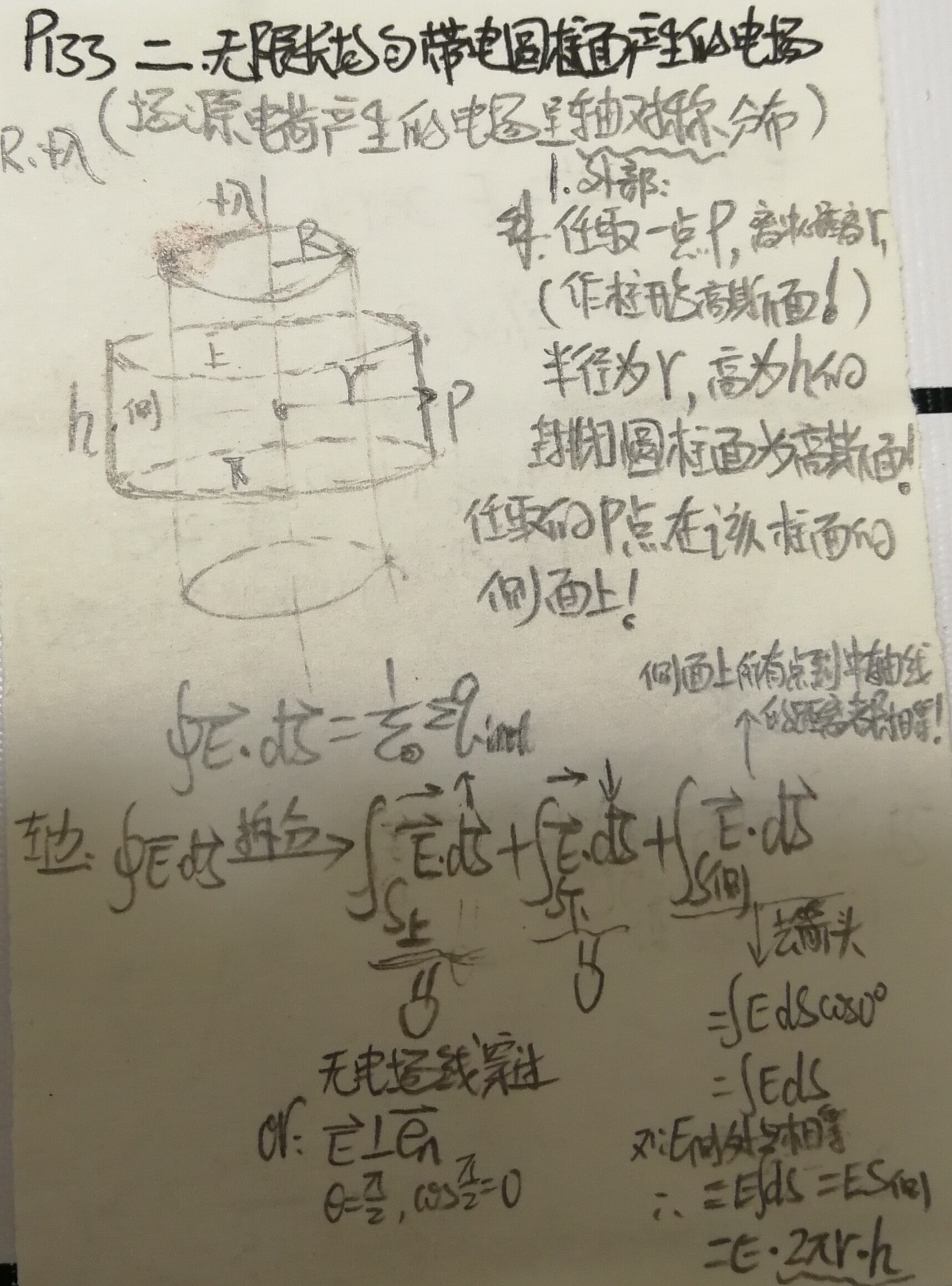
To calculate the electric field outside the cylindrical surface, the cylindrical shell can be treated as equivalent to an infinitely long uniformly charged straight line.

Note that the result is a uniform electric field. For a pair of infinitely large charged planes, simply multiply the result by 2.

Charged Sphere

Electric Potential

Let a positive charge be $q$, at a distance $r_{p_1}$ there is a point $p_1$ with electric potential ${\phi }_1$, and at a distance $r_{p_2}$ there is a point $p_2$ with electric potential ${\phi }_2$. Then:

${\phi }_a={\int }_a^{\mathrm{\infty }}\overrightarrow{E}\cdot \mathrm{d}\overrightarrow{l}$. Usually, in our exam questions, $\overrightarrow{E}$ and $\overrightarrow{l}$ are in the same direction, so the vector arrows can be directly removed.

Electric potential is a scalar quantity and can be directly summed.

$$A_{12}=W_1-W_2={\int }_{r_{p_1}}^{r_{p_2}}\overrightarrow{F}\cdot \mathrm{d}\overrightarrow{r}=q{\int }_{r_{p_1}}^{r_{p_2}}\overrightarrow{E}\cdot \mathrm{d}\overrightarrow{r}$$$$\frac{A_{12}}{q}={\phi }_{p_1}-{\phi }_{p_2}=|\mathrm{\Delta }{\phi }_{p_1{p}_2}|$$

Common Electric Potentials

Electric potential of a point charge: $\phi =\frac{1}{4\pi {\epsilon }_0}\frac{q}{r}$

Electric potential distribution of a continuous charged body: $\phi =\frac{1}{4\pi {\epsilon }_0}\int \frac{\mathrm{d}q}{r}$

The electric potential inside a charged spherical shell is uniform (since the electric field inside is zero). Outside the shell, the potential is inversely proportional to the distance from the center.

For a thin charged ring with charge $q$, simply replace $r$ with $\sqrt{R^2+x^2}$ to obtain its electric potential.

Finding Electric Field from Electric Potential

$$\overrightarrow{E}=-\frac{\partial \phi }{\partial n}\overrightarrow{e_n}=-\mathrm{\nabla }\phi$$

In most cases, only the one-dimensional case is considered, i.e., the case of $-\frac{\mathrm{d}\phi }{\mathrm{d}n}\overrightarrow{e_n}$.

Its magnitude is given by $|-\frac{\mathrm{d}\phi }{\mathrm{d}n}\overrightarrow{e_n}|=-\frac{\mathrm{d}\phi }{\mathrm{d}n}$, and its direction is given by $\overrightarrow{e_n}$.

Chapter 6

Electrostatic Equilibrium of Conductors

If two charged bodies are sufficiently far apart, they can be considered to have equal electric potentials.

If an object is grounded, it means the object has zero electric potential, but this does not imply that the object has no induced charge.

Capacitors and Capacitance

First, the definition of capacitance is given by $C=\frac{Q}{U}$, which is the same as in high school physics.

For a parallel-plate capacitor, with surface charge density $\sigma$:

$$U_{AB}={\int }_A^B\overrightarrow{E}\cdot \mathrm{d}\overrightarrow{r}=Ed=\frac{\sigma d}{{\epsilon }_0}$$$$C=\frac{Q}{U_{AB}}=\frac{{\epsilon }_{0}S}{d}$$

For a spherical capacitor, assuming the two spherical shells carry charges $\pm q$:

$$U_{AB}={\int }_A^B\overrightarrow{E}\cdot \mathrm{d}\overrightarrow{r}={\int }_{R_1}^{R_2}\frac{q}{4\pi {\epsilon }_0{r}^2}\mathrm{d}r=\frac{q}{4\pi {\epsilon }_0}(\frac{1}{R_1}-\frac{1}{R_2})$$$$C=\frac{Q}{U_{AB}}=\frac{4\pi {\epsilon }_0{R}_1{R}_2}{R_2-R_1}$$

In particular, the capacitance of an isolated spherical conductor is $4\pi {\epsilon }_{0}R$, which corresponds to the case where $R_2$ tends to infinity.

For capacitors in series, the reciprocal of the equivalent capacitance equals the sum of the reciprocals of the individual capacitances.

For capacitors in parallel, the equivalent capacitance equals the sum of the individual capacitances. (This is the opposite of resistors.)

Dielectrics in Electrostatic Fields

Relationships between several new physical quantities ${\overrightarrow{E}}_{\text{source}}$, ${\overrightarrow{E}}_{\text{new}}$, $\overrightarrow{D}$, ${\sigma }_0$, $\overrightarrow{P}$, ${\sigma }^{\prime }$ (where ${\epsilon }_r$ is the relative permittivity):

$$E_{\text{source}}={\epsilon }_r{E}_{\text{new}}$$$${\sigma }_0=D={\epsilon }_0{\epsilon }_r{E}_{\text{new}}$$$$P=({\epsilon }_r-1){\epsilon }_0{E}_{\text{new}}$$$${\sigma }^{\prime }=\pm P$$

Introducing the electric displacement vector $\overrightarrow{D}={\epsilon }_0\overrightarrow{E}+\overrightarrow{P}$, we have Gauss's law for $\overrightarrow{D}$:

$${\oint }_S\overrightarrow{D}\cdot \mathrm{d}\overrightarrow{S}=\mathrm{\Sigma }{q}_{0i}$$

Note: There is no $\frac{1}{{\epsilon }_0}$ on the right-hand side.

Electrostatic Energy Calculation

• Using electric potential:

$$W_e=\frac{1}{2}\mathrm{\Sigma }{q}_i{\phi }_i/\frac{1}{2}\int \phi \mathrm{d}q,\mathrm{d}q=\lambda \mathrm{d}l/\sigma \mathrm{d}S/\rho \mathrm{d}V$$

• Using energy density:

$$w_e=\frac{1}{2}{\epsilon }_0{E}^2=\frac{1}{2}{\epsilon }_0{\epsilon }_r{E}^2=\frac{1}{2}DE$$$$W_e=\int \mathrm{d}{w}_e={\int }_V{W}_e\mathrm{d}V$$

• For capacitors:

$$W_e=\frac{Q^2}{2C}=\frac{1}{2}QU=\frac{1}{2}C{U}^2$$

Chapter 7

Constant Current

The differential formula for current: $I=\frac{\mathrm{d}q}{\mathrm{d}t}$

Current density: $\overrightarrow{j}=nq\overrightarrow{u}$

Current continuity equation: $\oint \overrightarrow{j}\cdot \mathrm{d}\overrightarrow{S}=-\frac{\mathrm{d}q}{\mathrm{d}t}=0$ (outflow), constant current

Differential form of Ohm's law: $\overrightarrow{j}=\gamma \overrightarrow{E}$

Integral form of resistance: $R={\int }_L\frac{\rho \mathrm{d}l}{s},\rho =\frac{1}{\gamma }$

Electromotive force (EMF): $ℰ={\int }_{-}^{+}\overrightarrow{E}\cdot \mathrm{d}\overrightarrow{l}=\frac{A}{q},A={\int }_{-}^{+}\overrightarrow{F}\cdot \mathrm{d}\overrightarrow{l},\overrightarrow{F}=q\overrightarrow{E}$. Note that the forces here are all non-electrostatic forces, and the direction of $ℰ$ is from the negative terminal to the positive terminal of the power source.

Biot–Savart Law and Common Magnetic Field Strengths (1)

$\mathrm{d}B=\frac{{\mu }_0}{4\pi }\frac{I\mathrm{d}\overrightarrow{l}\times \overrightarrow{e_r}}{r^2}$, where $I\mathrm{d}\overrightarrow{l}$ is the current element, and the direction of $\overrightarrow{e_r}$ is from the current source to the point of interest.

$\overrightarrow{B}=\int \mathrm{d}\overrightarrow{B}=\int \frac{{\mu }_0}{4\pi }\frac{I\mathrm{d}\overrightarrow{l}\times \overrightarrow{e_r}}{r^2}$

For convenience, the arrow above $B$ is omitted below.

Infinitely Long Current-Carrying Wire

$B=\frac{{\mu }_{0}I}{2\pi r_0}$; for a semi-infinite wire, divide by 2.

Magnetic Field on the Axis of a Current-Carrying Circular Coil

$B=\frac{{\mu }_{0}I{R}^2}{2r^3},r=\sqrt{R^2+x^2}$

When $x=0$, $B=\frac{{\mu }_{0}I}{2R}$

A Point on the Axis of a Long, Closely Wound Solenoid

$B=\frac{{\mu }_{0}nI}{2}(\sin {\beta }_2-\sin {\beta }_1)$, where $\beta$ is the angle with the positive y-axis.

For an infinitely long solenoid, $B={\mu }_{0}nI$; for a semi-infinitely long one, divide by 2.

Ampere's Circuital Theorem and Common Magnetic Field Strengths (2)

Ampere's circuital theorem (analogous to Gauss's theorem): ${\oint }_L\overrightarrow{B}\cdot \mathrm{d}\overrightarrow{l}={\mu }_0\mathrm{\Sigma }{I}_{int}$

Infinitely Long Cylinder

Inside the cylinder: $B=\frac{{\mu }_{0}Ir}{2\pi R^2}=B_{out}\frac{r^2}{R^2}$

Outside the cylinder: $B=\frac{{\mu }_{0}I}{2\pi r}$

Infinitely Long Straight Solenoid & Toroidal Coil

According to Ampère's circuital law, by taking either a circular or a rectangular loop and applying appropriate approximations, the magnetic field can be derived as:

$B={\mu }_{0}nI$

where $n=\frac{N}{l}$ or $n=\frac{N}{2\pi r}$, with $N$ being the number of turns of the coil.

Infinitely Large Current-Carrying Plane

$B=\frac{1}{2}{\mu }_{0}j$

Thus, both sides of an infinitely large current-carrying plane exhibit a uniform magnetic field.

Displacement Current and Total Current

The current formed by the directional movement of charges is called the conduction current $I_c$, while a changing electric field is equivalent to the displacement current $I_d$.

Displacement current density: $\overrightarrow{j_d}={\epsilon }_0{\epsilon }_r\frac{\mathrm{d}\overrightarrow{E}}{\mathrm{d}t}$

Displacement current: $I_d={\int }_s\overrightarrow{j_d}\cdot \mathrm{d}\overrightarrow{s}={\epsilon }_0{\epsilon }_r\frac{\mathrm{d}}{\mathrm{d}t}\int \overrightarrow{E}\cdot \mathrm{d}\overrightarrow{s}={\epsilon }_0{\epsilon }_r\frac{\mathrm{d}{\phi }_e}{\mathrm{d}t}$

Generalized Ampère's circuital law: ${\oint }_L\overrightarrow{B}\cdot \mathrm{d}\overrightarrow{l}={\mu }_0(I_c+I_d)$

Force on a Moving Charge in a Magnetic Field

Lorentz force: $\overrightarrow{f}=q\overrightarrow{v}\times \overrightarrow{B}$

Uniform Circular Motion in a Uniform Magnetic Field

• $R=\frac{mv}{qB}$
• $T=\frac{2\pi m}{qB}$
• Pitch $h=v_{\parallel }\cos \theta$

Hall Effect

The Hall potential difference is given by $U_H=\kappa \frac{BI}{d}$, and the Hall coefficient is $\kappa =\frac{1}{nq}$.

Determining N-type and P-type: (To be filled)

Force on a Current-Carrying Conductor in a Magnetic Field

Non-closed type: $\overrightarrow{F}=\int \mathrm{d}\overrightarrow{F}={\int }_{L}I\mathrm{d}\overrightarrow{l}\times \overrightarrow{B}$

Closed type (circular, rectangular):

• Magnetic moment: $\overrightarrow{m}=IS\overrightarrow{e_n}$
• Magnetic torque: $\overrightarrow{M}=\overrightarrow{m}\times \overrightarrow{B}$ (The main difficulty lies in determining the direction)

Magnetic Media

An electron orbiting the nucleus possesses two magnetic moments: one is the orbital magnetic moment due to its "revolution," and the other is the spin magnetic moment due to its "rotation." The former is larger than the latter.

Taking the orbital magnetic moment as an example, it can be equivalently represented as a ring current $i=\frac{e}{T}=\frac{e\omega }{2\pi }=\frac{v}{2\pi r}e$. Thus, the magnetic moment is $\overrightarrow{m}=iS\overrightarrow{e_n}=-\frac{e{r}^2}{2}\overrightarrow{\omega }$.

Introducing the magnetic field strength $\overrightarrow{H}=\frac{\overrightarrow{B}}{{\mu }_0}-\overrightarrow{M}$, the Ampere's circuital law for magnetic media is given by:

$${\oint }_L\overrightarrow{H}\cdot \mathrm{d}\overrightarrow{l}=\mathrm{\Sigma }{I}_c$$

Several new physical quantities (directions omitted below): magnetic field strength $H$, $B_{\text{new}}$, magnetization $M$, current density $j$, and current $I^{\prime }$. In paramagnetic materials, these five vectors share the same direction. The conversion relationships between these physical quantities are as follows:

$$B_{\text{new}}={\mu }_0{\mu }_{r}H$$$$M=\frac{{\mu }_r-1}{{\mu }_0{\mu }_r}{B}_{\text{new}}$$$$j^{\prime }=\pm M$$$$I^{\prime }=\int j^{\prime }\mathrm{d}l$$

Chapter 8

Faraday's Law of Electromagnetic Induction

$\mathrm{\Phi }=BS$

$$\mathcal{E}=-\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}$$

The negative sign is explained by Lenz's law (opposing the change in magnetic flux).

Induced current

$$i=\frac{\mathcal{E}}{R}=-\frac{1}{R}\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}$$

Induced charge

$$q={\int }_{t_1}^{t_2}i\mathrm{d}t$$

Motional Electromotive Force

$$\mathcal{E}={\int }_L(\overrightarrow{v}\times \overrightarrow{B})\cdot \mathrm{d}\overrightarrow{l}$$

Electric motor: $\mathcal{E}I\mathrm{d}t=I^{2}R\mathrm{d}t+I\mathrm{d}\mathrm{\Phi }$, where $I\mathrm{d}\mathrm{\Phi }$ represents useful work.

Faraday disk generator: $\mathcal{E}=\frac{1}{2}B\omega R^2$, with the direction from the center to the edge.

$N$-turn closed loop rotating: $\mathcal{E}=\omega NBS\sin \omega t$

Induced Electromotive Force

Faraday's experimental formula: $\mathcal{E}=-\frac{\mathrm{d}{\mathrm{\Phi }}_m}{\mathrm{d}t}$

Maxwell's theoretical formula: $\mathcal{E}=\oint \overrightarrow{E_i}\cdot \mathrm{d}\overrightarrow{l}$

A changing magnetic field induces an electric field: $\oint \overrightarrow{E_i}\cdot \mathrm{d}\overrightarrow{l}=-{\int }_S\frac{\mathrm{d}\overrightarrow{B}}{\mathrm{d}t}\cdot \mathrm{d}\overrightarrow{S}$

Self-Inductance and Mutual Inductance

1. In both cases, first find the expression for magnetic flux.
2. The coefficient in front of the current is either $L$ or $M$.
3. The first derivative of magnetic flux with respect to time is ${\mathcal{E}}_L$ or ${\mathcal{E}}_M$.

Self-Inductance

$${\mathrm{\Psi }}_m=N{\mathrm{\Phi }}_m=LI$$$${\mathcal{E}}_L=-\frac{\mathrm{d}{\mathrm{\Psi }}_m}{\mathrm{d}t}=-L\frac{\mathrm{d}I}{\mathrm{d}t}$$

Mutual Inductance

$${\mathrm{\Psi }}_{m2}=N{\mathrm{\Phi }}_m=M{I}_1$$$${\mathcal{E}}_2=-\frac{\mathrm{d}{\mathrm{\Psi }}_{m2}}{\mathrm{d}t}=-M\frac{\mathrm{d}{I}_1}{\mathrm{d}t}$$$$M=\sqrt{L_1{L}_2}$$

Energy

Energy density $w_m=\frac{1}{2{\mu }_0{\mu }_r}{B}^2=\frac{1}{2}BH$

Total energy $W_m=\int w_m\mathrm{d}V$

For an RL circuit:

$${\int }_0^{\mathrm{\infty }}{\mathcal{E}}_{i}i\mathrm{d}t={\int }_0^{\mathrm{\infty }}{\mathcal{E}}_{L}i\mathrm{d}t+{\int }_0^{\mathrm{\infty }}R{i}^2\mathrm{d}t$$

(Total energy from the power supply = Energy stored in the inductor + Energy dissipated by the resistor)

Maxwell's Equations

$$\oint \overrightarrow{D}\cdot \mathrm{d}\overrightarrow{S}=\mathrm{\Sigma }{q}_0$$$$\oint \overrightarrow{E}\cdot \mathrm{d}\overrightarrow{l}=-\int \frac{\mathrm{d}\overrightarrow{B}}{\mathrm{d}t}\cdot \mathrm{d}\overrightarrow{S}$$$$\oint \overrightarrow{B}\cdot \mathrm{d}\overrightarrow{S}=0$$$$\oint \overrightarrow{H}\cdot \mathrm{d}\overrightarrow{l}=\mathrm{\Sigma }{i}_c+\int \frac{\mathrm{d}\overrightarrow{D}}{\mathrm{d}t}\cdot \mathrm{d}\overrightarrow{S}$$

where

$$\overrightarrow{D}={\epsilon }_0{\epsilon }_r\overrightarrow{E}$$$$\overrightarrow{H}=\frac{1}{{\epsilon }_0{\epsilon }_r}\overrightarrow{B}$$$$\overrightarrow{j}=\gamma \overrightarrow{E}$$