从一道 leetcode 题到离散对数求解算法

发表于 2025-03-18 分类于笔记阅读次数：本文字数： 9.3k 阅读时长 ≈ 8 分钟

我们先来看题面，点进去之前可以先思考一下：

Given an array of integers nums containing $n + 1$ integers where each integer is in the range $[1, n]$ inclusive, $n \le 10^5$ .

There is only one repeated number in nums, return this repeated number.

You must solve the problem without modifying the array and using only constant extra space.

算法题解答

如果不看第三行，那么任意 $O(n \log n)$ 的排序都可以做这道题。即使不限制 $O(1)$ 的空间的话，因为元素在 $[1, n]$ 之间，桶排序也是可以 AC 的。但如果既不能修改数组 nums，也不能新开数组，那就只能考虑双指针解法了。

一个比较容易想到的做法是 binary search，既然值域在 $[1, n]$ ，我们可以令 $mid = \lfloor\frac{1+n}{2}\rfloor$ ，然后取 num 中的元素的个数（记为 $x$ ），如果 $x \le mid$ 。我们可以证明 $[1, mid]$ 之间没有重复元素：

这里使用反证法，记 $[condition]$ 为当“condition”为真时值为 $1$ ，否则为 $0$ 。

假设 $[1, mid]$ 之间存在重复元素且 $\sum_{i=1}^n [num_i \le mid] = x$ 。因为重复元素只有一个，因此 $[mid+1, n]$ 这些元素只会存在 $0$ 个或者 $1$ 个。因此 $\sum_{i=1}^n [num_i > mid] \le n - mid$ ，两式相加可得 $n+1 \le x + n - mid \le n$ ，矛盾！

因此假设不成立，原结论正确， $[1, mid]$ 之间没有重复元素。

有了上述的结论，我们可以断定当 $x \le mid$ 时，应当继续在 $[mid+1, n]$ 中寻找。而当 $x > mid$ 时，根据抽屉原理显然 $[1, mid]$ 之间有重复元素，应当在 $[1, mid]$ 中继续搜索。

以上过程递归进行，总时间复杂度为 $O(n \log n)$ 。

def findDuplicate(self, nums: List[int]) -> int:
    low, high = 1, len(nums) - 1
    
    while low < high:
        mid = (low + high) // 2
        count = 0
        for num in nums:
            if num <= mid:
                count += 1
        if count > mid:
            high = mid
        else:
            low = mid + 1
            
    return low

Floyd’s cycle-finding algorithm

但题面中还有一个 follow up:

Can you solve the problem in linear runtime complexity?

这便是 binary search 不能触及到的领域了。这里我选择直接放弃，然后知道了一个名为 Floyd’s cycle-finding 的算法，它也有一个别名叫 tortoise and the hare algorithm：算法过程如下：

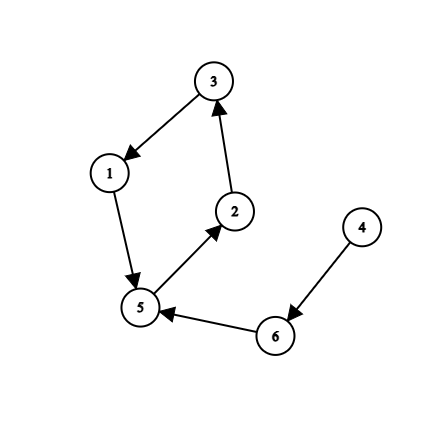
首先根据 nums 数组建图，数组的 index 是一个端点（这里 index 从 1 开始），而这个 index 对应的值则是这个端点指向的端点。例如以下数组：

1	[5,3,1,6,2,5]

对应了以下这个有向图：

首先 hare 和 tortoise 随机选一个点同时出发（为了演示方便，这里选择 4 号点），此时 hare 跑得快些，一次跑两步，tortoise 速度慢些，一次爬一步。于是便会有这样的情景（左 hare，右 tortoise）：

这个时候 hare 与 tortoise 正式相遇了，这说明算法成功找到了一个环（不然 hare 只会永远在 tortoise 前面）。

然后算法的下一步为了找到环的“起始点”（也就是点 5。如果他们一开始就在环里那自然就是起点了）。将 tortoise 放回了起点 4，hare 保持原先位置 3 不动，随后它们每次走一步：

1
2
3

3 4
1 6
5 5

可以发现它们在环的“起始点” 5 处相遇了。可以证明，无论图的形状如何，它们始终都会在环的“起始点”处相遇：

设环的周长为 $C$ ，尾巴（也就是图中 5->6->4 的长度为 $d$ ）当他们第一次相遇时，hare 走了 $2t$ 步，tortoise 走了 $t$ 步，显然我们有 $C | (2t - t)$ 。而当 tortoise 被移回起点时，由于此时它们速度一样，hare 和 tortoise 的距离就恒为 $2t$ 。当 tortoise 走了 $d$ 步到了“起始点”时，hare 走了 $2t+d$ 步，由于 $C | 2t$ ，因此 hare 和 tortoise 必相遇，并且都在“起始点”。

算法的最后一步就是 hare 不动，tortoise 绕一圈测出周长 $C$ ，这个算法就结束了。

回到本题，由于重复的数字只有一个，所以肯定是“起始点”本身，因此我们只需要做算法的前两步即可 AC。时间复杂度 $O(n)$ 。

def findDuplicate(self, nums: List[int]) -> int:
    slow = nums[0]
    fast = nums[0]
    while True:
        slow = nums[slow]
        fast = nums[nums[fast]]
        if slow == fast:
            break
    fast = nums[0]
    while slow != fast:
        slow = nums[slow]
        fast = nums[fast]
    return fast

Brent’s algorithm

Brent 在 Floyd 的探圈算法基础上进行了改进，使用了 2 的幂次步长power来检测循环。并引入了lambda（每次迭代自增，可以理解为周长 $C$ ）和 mu（自增，最后得出尾巴 $d$ 的值）。该算法的优势有两点：

直接在第一步找到了环的周长 $C$ 。
每一次迭代只需要计算一次 $f$ ，而不是 floyd 的三次。

举一个例子，如果图长这样（假设它们都从 1 开始）：

1	1 -> 2 -> 3 -> 4 -> 5 -> 3

然后我们有：

Frame 1: Tortoise at 1, Hare at 2, power = 1, lambda = 1.
Frame 2: Tortoise at 2, Hare at 3, power = 2, lambda = 1.
Frame 3: Tortoise at 2, Hare at 4, power = 2, lambda = 2.
Frame 4: Tortoise at 4, Hare at 5, power = 4, lambda = 1.
Frame 5: Tortoise at 4, Hare at 3, power = 4, lambda = 2.
Frame 6: Tortoise at 4, Hare at 4, power = 4, lambda = 3 (cycle length detected).
Frame 7: Tortoise at 1, Hare at 1 (reset for finding position of length lambda).
Frame 8: Tortoise at 1, Hare at 2.
Frame 9: Tortoise at 1, Hare at 3.
Frame 10: Tortoise at 1, Hare at 4. (repeated lambda times)
Frame 11: Tortoise at 2, Hare at 5, mu = 1.
Frame 12: Tortoise at 3, Hare at 3, mu = 2. (cycle start found)

python 代码如下：

def brent(f, x0) -> (int, int):
    """Brent's cycle detection algorithm."""
    # main phase: search successive powers of two
    power = lam = 1
    tortoise = x0
    hare = f(x0)  # f(x0) is the element/node next to x0.
    # this assumes there is a cycle; otherwise this loop won't terminate
    while tortoise != hare:
        if power == lam:  # time to start a new power of two?
            tortoise = hare
            power *= 2
            lam = 0
        hare = f(hare)
        lam += 1

    # Find the position of the first repetition of length λ
    tortoise = hare = x0
    for i in range(lam):
    # range(lam) produces a list with the values 0, 1, ... , lam-1
        hare = f(hare)
    # The distance between the hare and tortoise is now λ.

    # Next, the hare and tortoise move at same speed until they agree
    mu = 0
    while tortoise != hare:
        tortoise = f(tortoise)
        hare = f(hare)
        mu += 1
 
    return lam, mu

pollard_rho

由于这个建图很容易让人想起 $\rho$ 这个希腊字母，刚好 Pollard 本人也是这么想的。于是他找到了一个代数结构：有限环 $R_n$ ，然后加了一个运算 $f(x) = (x^2+t) \mod n$ 用来生成一个伪随机序列 $A = [x, f(x), f^2(x), \cdots]$ 。如果 $n=pq$ ，那么我们假设这个随机序列在 $[A_i \mod p]$ 中均匀分布，根据生日悖论，我们期望在 $O(\sqrt{p})$ 的时间内找到一对相同的值。

那么我们如何来遍历这里的 $i,j$ （hare and tortoise）呢，虽然序列 $A$ 是 $\mod n$ 的，但考虑 $A_i \mod p$ 与 $A_j \mod p$ ，因为 $F_p$ 是一个域，对一个元素反复做运算 $f$ ，一定会形成一个周期（或者叫“轨道”）。这样的话，Floyd’s cycle-finding 就派上用场了，在经过有限次的迭代后，可能在 $F_p$ 中 $i,j$ 先相遇返回结果 $p$ 。同理，或者在 $F_q$ 中先相遇返回结果 $q$ 。或者也有可能会在 $R_n$ 中相遇返回结果 $n$ ，然而这个结果是平凡的，需要重新执行该算法。

这个算法便称为 pollard_rho 素性检测，因为 $p$ 在最坏的情况是 $O(\sqrt{n})$ 的，因此这个时候 pollard_rho 的平均时间复杂度为 $O(n^{1/4})$ 。

from math import *

def f(x, c, n):
    return (x * x + c) % n

def pollard_rho(n, max_attempts=10):
    if n % 2 == 0:
        return 2                    # tackle even case
    
    for attempt in range(max_attempts):
        x = random.randint(1, n-1)  # tortoise
        y = x                       # hare
        c = random.randint(1, n-1)  # c of f(x)
        g = 1                       # GCD result

        # Floyd's cycle-finding
        while g == 1:
            x = f(x, c, n)          # tortoise takes 1 step
            y = f(f(y, c, n), c, n) # hare takes 2 steps
            g = gcd(abs(x - y), n)  # calculate gcd

        if 1 < g < n:
            return g                # non-trivial divisor
        # retry
        
    return n                        # max retries exceeded

pollard_rho using Brent

为了水一篇论文，Brent 也使用了自己的算法替换了 pollard_rho 中的 Floyd 的探圈方法，并用实验证明了他的探圈方法效率比 Floyd 提高了 36%，从而导致总共的运行效率提高了 24%。

这里就不贴代码了，一种可能的实现参见：

https://comeoncodeon.wordpress.com/2010/09/18/pollard-rho-brent-integer-factorization/

pollard_rho for DLP

就像将质因数分解问题联想到 DLP（离散对数问题）那样自然一样，除了在有限环 $R_n$ 中做 pollard_rho 以分解质因数 $n$ 之外，Pollard 本人还将该方法论尝试在 DLP 中得到应用。

我们假设需要求解离散对数问题 $\alpha^\gamma=\beta \pmod n$ ，这里 $n$ 为素数。我们可以寻找 $a,b,A,B$ 来满足 $\alpha^a \beta^b = \alpha^A \beta^B$ ，从而我们代入上式，有：

\alpha^a \alpha^{\gamma b} = \alpha^A \alpha^{\gamma B}

根据欧拉定理，我们有：

a + \gamma b = A + \gamma B \pmod{n-1}

(B-b)\gamma = a - A \pmod{n-1}

就可以通过 exgcd 求出对应的 $\gamma$ 。

而对于如何找到这样的 $a,b,A,B$ ，关键在于如何选取 $\mathbb{F}_n\rightarrow\mathbb{F}_n$ 的映射（类比于之前的 $f(x) = x^2+t \mod n$ ），使得 $x_i = \alpha^{a_i} \beta^{b_i}$ 在 $\mathbb{F}_n$ 上足够均匀。Pollard 本人给出了一种映射方式，但他并没有说明这种映射方式充分均匀随机：

f(x) = \begin{cases} \alpha x, & \text{if } 0 \leq x < p/3, \\ x^2, & \text{if } p/3 \leq x < 2p/3, \\ \beta x, & \text{if } 2p/3 \leq x < p. \end{cases}

这里我们使用这个公式的变种：

f(x) = \begin{cases} x^2, & \text{if } x \equiv 0 \mod 3, \\ \alpha x, & \text{if } x \equiv 1 \mod 3, \\ \beta x, & \text{if } x \equiv 2 \mod 3. \end{cases}

然后设初始值 tortoise 为 $x=1,a=0,b=0$ ，hare 为 $X=x, A=a, B=b$ ，建立伪随机序列 $A = [1, f(x), f^2(x), \cdots]$ 。这个时候请出我们的 Floyd’s cycle-finding 算法，分别计算 $X = f^2(X), x = f(x)$ 。然后对应地去调整相应的 $a,b,A,B$ （聪明的你应该知道怎么去调整），最后在有限次迭代中可以找到 $\alpha^a \beta^b = \alpha^A \beta^B$ 的一个碰撞。

以下是 $n = 1019, \alpha = 2, \beta = 5$ 的一个例子，以下每一行是 $x$ 迭代一次， $X$ 迭代两次的结果：

 i     x   a   b     X   A   B
------------------------------
 1     2   1   0    10   1   1
 2    10   1   1   100   2   2
 3    20   2   1  1000   3   3
 4   100   2   2   425   8   6
 5   200   3   2   436  16  14
 6  1000   3   3   284  17  15
 7   981   4   3   986  17  17
 8   425   8   6   194  17  19
..............................
48   224 680 376    86 299 412
49   101 680 377   860 300 413
50   505 680 378   101 300 415
51  1010 681 378  1010 301 416

可以看到当 $a, b, A, B = 681, 378, 301, 416$ 时发生了碰撞，此时代入 $(B-b)\gamma = a - A \pmod{n-1}$ 可得 $38 \gamma = 380$ ，可得 $\gamma = 10$ 或 $519$ （舍去）。

于是我们就在约 $\frac{\sqrt{\tau n}}{2}$ 步后（ $\tau = 2\pi$ ）找到了一个碰撞（不会证），因此算法的复杂度为 $O(\sqrt{n})$ ，与确定性算法 BSGS (大步小步算法相同)。

DLP 与 pohlig-hellman 算法结合

pohlig-hellman 算法也可以用于高效求解 DLP 问题，主要思路将 $n-1$ 进行质因数分解，然后使用某种算法（链接里使用了 BSGS）来进行 $\mathrm{GF}(p)$ 中离散对数的求解，最后用 CRT（中国剩余定理）合并各个质数 $p$ 的结果。具体的介绍阮行止写得很好，可以去看一看：

https://www.ruanx.net/pohlig-hellman/

若知道 DLP 中 $n-1$ 的质因数分解方法，则可以使用该算法与先前的 pollard_rho 算法结合，将 DLP 求解时间复杂度从 pollard_rho 的 DLP 版本的时间复杂度从 $O(\sqrt{n})$ 降低至 $O(\sqrt{p})$ ，其中 $p$ 是 $n-1$ 的最大质因数。

因此综上所述 DLP 这个问题取决于 $n-1$ 本身是否光滑，对于通用 $n$ （例如大素数），时间复杂度是Pollard’s Rho 或 BSGS 的 $O(\sqrt{n})$ ，如果 $n$ 已分解为 $\prod p_i^{e_i}$ ，则时间复杂度为 $O(\sum e_i \sqrt{p_i})$ 。