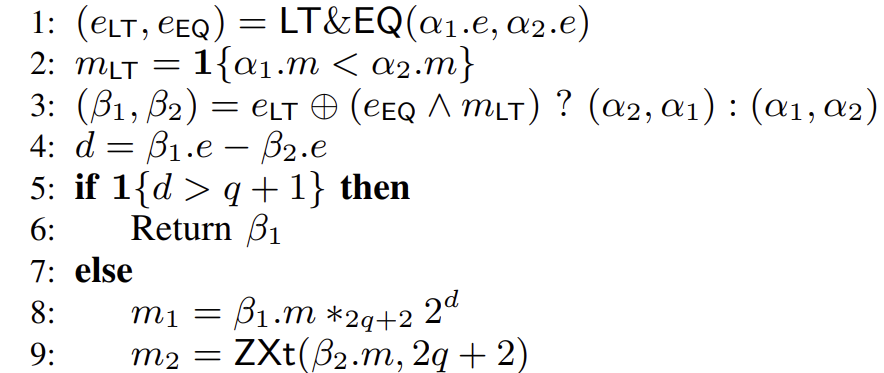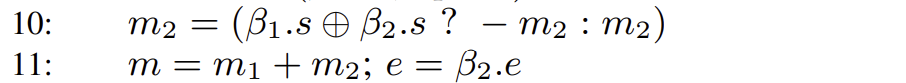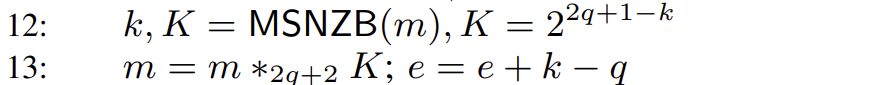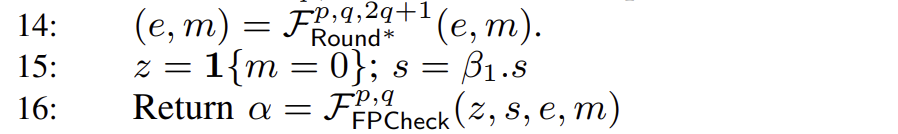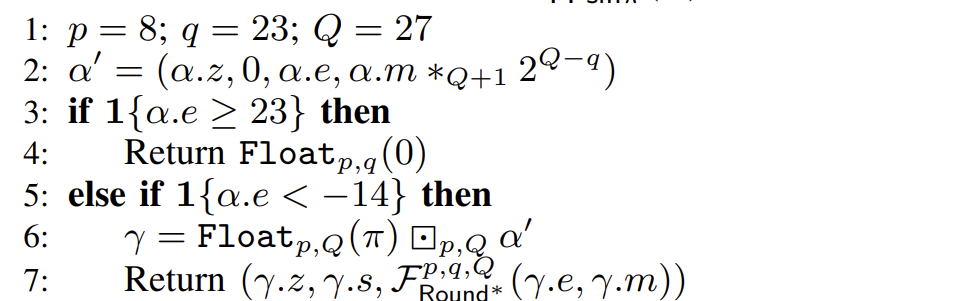English
Rathee 三部曲:CrypTFlow2,SIRNN与SecFloat
Background
Notation: 记安全参数为 λ l
MPC方面,假设我们拥有以下基础知识:
可以使用基于公钥密码等方式实现 1-out-of-k OT l 2 λ + k l λ + k l
基于 2-party 的加法 secret sharing 的加法与标量乘几乎免费(无通信开销)。
可以使用 beaver triple 实现 2-party 的安全乘法操作。一次安全乘法,总通信量为 2 l
在浮点数储存方面,我们使用 IEEE754 Float32(单精度标准):
( − 1 ) S × ( 1. M ) × 2 E − b i a s 符号位 S E M b i a s = 127
四舍六入五成双(round-to-nearest-ties-to-even)
IEEE 754 加法
不失一般性,设 x ≥ y z = x + y
x = ( − 1 ) S x ⋅ ( 1. M x ) ⋅ 2 E x , y = ( − 1 ) S y ⋅ ( 1. M y ) ⋅ 2 E y 则步骤如下:
指数对齐。若 E x E y y M y ← 1. M y 2 E x − E y , E ← E x , M x ← ( 1. M x )
尾数相加。考虑S x , S y M = M x + M y M = | M x − M y | S
规范化。显然 max { M x + M y , | M x − M y | } < 4 M E M = 0 E M ∈ [ 1 , 2 )
写入结果。最后将 M S , E , M
在 M y ← 1. M y 2 E x − E y M = M x + M y M = | M x − M y | M
IEEE 754 乘法
乘法由于不涉及数的大小比较,因此步骤相对比较简单。
符号位异或。S = S x ⊕ S y
指数相加。E = E x + E y − b i a s
尾数相乘。M = ( 1. M x ) ⋅ ( 1. M y ) [ 1 , 4 )
规范化。如果结果 ≥ 2 E M M
在 M = ( 1. M x ) ⋅ ( 1. M y ) M
舍入方法
我们令 d , g , f M
c = g ∧ ( d ∨ f ) 简单的解释一下,就是只有当 g = 1 f = 1 d = 1 0.5 c = 1
注意舍入之后有可能需要再次规范化。
Building Blocks
下面用自底向上的方式,讲清楚整个协议是如何构建的。
F M U X 我们需要实现的理想功能是,MUX(b,x)=(b==1?x:0)。即对于布尔 secret share [ c ] = ( c 0 , c 1 ) , c i ∈ { 0 , 1 } [ a ] = ( a 0 , a 1 ) , a ∈ Z n [ a ⋅ c ]
SETUP: P 0 a 0 , c 0 P 1 a 1 , c 1
P 0 P 1 r 0 , r 1 ∈ Z n P 0 c 0 ( s 0 , s 1 ) c 0 = 0 ( s 0 , s 1 ) = ( − r 0 , − r 0 + a 0 ) ( − r 0 + a 0 , − r 0 ) P 0 P 1 P 0 ( s 0 , s 1 ) P 1 c 1 x 1 = s c 1 P 1 c 1 ( t 0 , t 1 ) c 1 = 0 ( t 0 , t 1 ) = ( − r 1 , − r 1 + a 1 ) ( − r 1 + a 1 , − r 1 ) 再做一轮 OT,P 0 x 0 = t c 0
P 0 r 0 + x 0 P 1 r 1 + x 1 ( r 0 + r 1 ) + ( x 0 + x 1 )
我们列举出四种可能的 ( c 0 , c 1 )
( s 0 , s 1 ) = ( − r 0 + c 0 a 0 , − r 0 + a 0 ( 1 − c 0 ) ) ( t 0 , t 1 ) = ( − r 1 + c 1 a 1 , − r 1 + a 1 ( 1 − c 1 ) )
x 0 = t c 0 , x 1 = s c 1
c 0 c 1 x 0 x 1 ( r 0 + r 1 ) + ( x 0 + x 1 )
0
0
− r 1 + c 1 a 1 − r 0 + c 0 a 0 0
0
1
− r 1 + c 1 a 1 − r 0 + a 0 ( 1 − c 0 ) a
1
0
− r 1 + a 1 ( 1 − c 1 ) − r 0 + c 0 a 0 a
1
1
− r 1 + a 1 ( 1 − c 1 ) − r 0 + a 0 ( 1 − c 0 ) 0
结果刚好等于 [ a ⋅ c ]
通信量为两轮 IKNP-OT 的开销,也就是 2 ( λ + 2 l ) = 2 λ + 4 l 2 λ + 2 l
F A N D 这是显然的,直接使用 beaver triple 实现,通信量为 ( λ + 16 ) + 4
F O R 我们有 [ x ∨ y ] = [ x ⊕ y ] ⊕ [ x ∧ y ] [ x ∧ y ] = ( z 0 , z 1 ) x i ⊕ y i ⊕ z i F A N D λ + 20
F E Q 我们将 x , y m x j , y j 2 m
P 0 ( e q 0 , j ) 0 k ∈ [ 0 , 2 m − 1 ] t j , k = ( e q 0 , j ) 0 ⊕ ( x j == k ) P 0 2 m P 1 y j ( e q 0 , j ) 1 当且仅当 x j = y j ( e q 0 , j ) 0 ⊕ ( e q 0 , j ) 1 = 1 x j , y j
我们可以通过树状结构与 F A N D ( e q 1 , j ) i = ( e q 0 , j ) i ∧ ( e q 0 , j + m ) i m 2 m ⌈ l m ⌉ ( 2 λ + 2 m ) + ⌈ l m ⌉ ( λ + 20 ) log l
F G T / L T 仍然是分块的思路,首先计算块长度为 m 1 { x j < y j } 2 m P 0 ( l t 0 , j ) 0 2 m t j , k = ( l t 0 , j ) 0 ⊕ 1 { x j < k }
然后合并的时候高位优先,1 { x < y } = 1 { x H < y H } ⊕ ( 1 { x H = y H } ∧ 1 { x L < y L } )
通信成本小于 λ ( 4 q ) + 2 m ( 2 q ) + 22 q m = 4 , q = l / 4 λ l + 13.5 l log l
F L U T 假设 LUT 有 2 m n
SETUP: P 0 r ∈ { 0 , 1 } m L T 0 [ i ] ∈ Z 2 n , ∀ i ∈ { 0 , 1 } m
P 0 s ∈ { 0 , 1 } m M s [ i ] = L [ i ⊕ r ⊕ s ] ⊕ T 0 [ i ] , ∀ i ∈ { 0 , 1 } m P 0 2 m n P 1 s 2 m OT n 2 λ + 2 m n P 1 T 1 ← M s P 0 ( T 0 , r ) P 1 ( T 1 , s ) 在线阶段,P 0 u = x 0 ⊕ r P 1 v = x 1 ⊕ s i ∗ = u ⊕ v = x ⊕ r ⊕ s P 0 , P 1 T 0 [ i ∗ ] , T 1 [ i ∗ ] L [ x ] 2 m
F W r a p 如果我们要计算 1 { a + b > 2 n − 1 } 1 { 2 n − 1 − a < b } F G T / L T
F B 2 A P 0 , P 1 c = c 0 ⊕ c 1 , c ∈ { 0 , 1 } d = d 0 + d 1 ( mod 2 n ) d = c
P 0 x ∈ Z 2 n ( x , c 0 + x ) P 1 c 1 COT n P 1 y 1 P 0 y 0 = 2 n − x 双方本地线性修正,P 0 d 0 = c 0 − 2 y 0 P 1 d 1 = c 1 − 2 y 1
验证一下结果,d 0 + d 1 = c 0 + c 1 − 2 ( y 0 + y 1 )
当 c 1 = 0 y 0 + y 1 = ( 2 n − x ) + x = 2 n d 0 + d 1 = c 0 + c 1 ( mod 2 n )
当 c 1 = 1 y 0 + y 1 = ( 2 n − x ) + ( c 0 + x ) = 2 n + c 0 d 0 + d 1 = c 0 + c 1 − 2 c 0 = 1 − c 0 c = c 0 ⊕ 1 = 1 − c 0 d = c
通信开销为一次 1-out-of-2 COT n λ + n
F Z E x t 我们有了前面的 F W r a p F B 2 A F Z E x t m n ( n > m ) F W r a p w F B 2 A Z 2 n − m
但我们只是做零扩展操作,两个 share 相加,不能在第 m Z 2 n 2 m m
成本为 Comm ( F W r a p + F B 2 A ) = λ m + 14 m + λ + ( n − m ) = λ ( m + 1 ) + 13 m + n
F T R 既然我们有了从小到大的 F Z E x t F T R l s l − s x >> s):
SETUP: P b x b u b | | v b l − s s
T R ( x , s ) = u 0 + u 1 + W r a p ( v 0 , v 1 , s ) 开销为 Comm ( F W r a p + F B 2 A ) = ( λ s + 14 s ) + ( λ + ( l − s ) ) = λ ( s + 1 ) + 13 s + l
F C r o s s T e r m F C r o s s T e r m P 0 P 1 x y F C r o s s T e r m P 0 x P 1 y l = m + n x ∗ y
P 0 x x = ∑ i = 0 m − 1 x i 2 i , x i ∈ { 0 , 1 } 对 i ∈ [ 0 , m − 1 ] COT l − i P 0 x i P 1 y ⟨ t i ⟩ l − i t i = x i ⋅ y
双方本地计算 ⟨ z ⟩ l = ∑ i = 0 m − 1 ⟨ t i ⟩ l − i x ⋅ y
总通信成本为 ∑ i = 0 m − 1 ( λ + ( l − i ) ) = m λ + m l − m ( m − 1 ) 2 = O ( m λ + m n )
F U M u l t 语义是双方持有 x = x 0 + x 1 ( mod 2 m ) , y = y 0 + y 1 ( mod 2 n ) z = x ⋅ y ∈ Z 2 m + n
这里还是不能直接做 beaver triple,因为它是 ring agnostic 的,可能会带来未知的 wrap 问题。当然一个办法是将 x , y F T R F U M u l t
我们现在要计算( x 0 + x 1 ) ( y 0 + y 1 ) = x 0 y 0 + x 1 y 1 + x 0 y 1 + x 1 y 0 P 0 , P 1 F C r o s s T e r m P 0 x 0 y 0 P 1 x 1 y 1 ⟨ x 0 y 1 ⟩ , ⟨ x 1 y 0 ⟩ F U M u l t
首先,我们要考虑 x 0 + x 1 , y 0 + y 1 F W r a p w x , w y
然后我们可以利用 F M U X g=w_y?x:0 与 h=w_x:y:0的 share ⟨ g ⟩ , ⟨ h ⟩
最终 P b x b y b + ⟨ x 0 y 1 ⟩ b + ⟨ x 1 y 0 ⟩ b − 2 n ⟨ g ⟩ b − 2 m ⟨ h ⟩ b
尝试把两个 share 加起来看看:∑ b ( x b y b + ⟨ x 0 y 1 ⟩ b + ⟨ x 1 y 0 ⟩ ) = ( x 0 + x 1 ) ( y 0 + y 1 )
而 ∑ b ( − 2 n ⟨ g ⟩ b − 2 m ⟨ h ⟩ b ) = − 2 n g − 2 m h = − 2 n ( w y ⋅ x ) − 2 m ( w x ⋅ y )
合在一起,z = ( x 0 + x 1 ) ( y 0 + y 1 ) − w y ⋅ ( x ⋅ 2 n ) − w x ⋅ ( y ⋅ 2 m )
= ( x + w x 2 m ) ( y + w y 2 n ) − w y ⋅ ( x ⋅ 2 n ) − w x ⋅ ( y ⋅ 2 m ) = x y
设ν = max ( m , n ) , l = m + n O ( λ ν + ν 2 ) O ( λ l + l 2 ) F U M u l t 1.5 ×
F S M u l t F U M u l t
F D i g D e c 作用是将一个 l ⟨ x ⟩ d c = ⌈ l d ⌉ { ⟨ z i ⟩ } i = 0 c − 1 x = z c − 1 | | z c − 2 | | ⋯ | | z 0
当然解决这个问题的思路也容易想到,首先使用 F w r a p ⟨ x [ 0 , d − 1 ] ⟩ ⟨ c 0 ⟩ ⟨ z 0 ⟩ = ⟨ x [ 0 , d − 1 ] ⟩ − 2 d ⟨ c 0 ⟩ ⟨ x [ d , l − 1 ] ⟩ ⟨ c 0 ⟩
复杂度相当于 ( c − 1 ) F w r a p ( c − 1 ) ( λ d + 14 d )
F M S N Z B − P 检测第 i d ⌊ log 2 ( z i ) ⌋ + i ⋅ d F L U T z i = 0 z i = 0
这一点我不是很理解,z i = 0 F L U T
总之,通信量等价于一个 1-out-of-2 d OT ⌈ log 2 l ⌉ 2 λ + 2 d ⌈ log 2 l ⌉
F Z e r o s , F O n e H o t 前者的意思是判断一个长度为 d d ⟨ k ⟩ ∈ [ 0 , l − 1 ] l ( 0 , 0 , ⋯ , 1 , ⋯ , 0 ) k
这两个分别可以用 1-out-of-2 d OT l OT l 2 λ + 2 d 2 λ + l 2 F M S N Z B
F M S N Z B 含义是给定一个输入 ⟨ x ⟩ l l k ( 0 , 0 , ⋯ , 1 , ⋯ , 0 ) k F M S N Z B − P z i = 0 ι = ⌈ log 2 l ⌉
首先计算输入 ⟨ x ⟩ l F D i g D e c ⟨ y i ⟩ d i F M S N Z B − P ⟨ u i ⟩ ι
调用 F Z e r o s ⟨ v i ⟩ F A N D i = c − 2 , ⋯ , 0 w i = w i + 1 ∧ v i + 1 w i = ∏ j > i v j w i = 1
对最高位 digit,令 ⟨ z c − 1 ′ ⟩ ι = ⟨ u c − 1 ⟩ ι i = c − 2 , ⋯ , 0 z i ′ = MUX ( w i , u i )
最后本地算出 z ~ = ∑ i = 0 c − 1 z i ′ F O n e H o t { ⟨ z k ⟩ } k ∈ [ 0 , l − 1 ]
总结
原语
依赖的原语
功能
通信开销
F M U X ( 2 1 ) − OT l 长度l
2 λ + 2 l
F O R F A N D , i.e. beaver triple 逻辑或
λ + 20
F E Q ( 2 m 1 ) − OT , F A N D 长度l
< 3 4 λ l + 9 l
F L T / G T ( 2 m 1 ) − OT , F A N D 长度l
< λ l + 14 l
F L U T ( 2 m 1 ) − OT n 长度m n
2 λ + 2 m n
F Z E x t F W r a p , F B 2 A m n λ ( m + 1 ) + 13 m + n
F T R F W r a p , F B 2 A l l − s λ ( s + 1 ) + l + 13 s
F U M u l t , F S M u l t F C r o s s T e r m , F W r a p , F M U X 长度m , n
O ( λ l + l 2 )
F M S N Z B 等 F D i g D e c , F M S N Z B − P , F O n e H o t 等 长度l
≤ λ ( 5 l − 4 ) + l 2
Primitives
我们终于构建了 secfloat 论文对应的所有基础协议,现在我们转入本篇论文构造的重要原语。
F F P c h e c k p , q 用来检查浮点数在浮点参数为 p , q p = 8 , q = 23 这是本文的一个创新点,就是可以自己选取浮点参数 ,不一定遵照 IEEE754 的格式。
α = (z, s, e, m)
if 1{e > 2^{p-1} - 1} then
m = 2^q; e = 2^{p-1}
if 1{z = 1} ∨ 1{e < 2 - 2^{p-1}} then
m = 0; e = 1 - 2^{p-1}; z = 1
Return (z, s, e, m)
这个逻辑符合论文对溢出的处理方式,这里大概描述一下协议是怎么跑的:
第二行由于 p F G T / L T F E Q
第三行和第五行的赋值操作,由于赋值常数c P 0 = 0 , P 1 = c
if 分支本质就是 F M U X
F T R S l , s F T R S F T R S s 1 L S B ( x ) = 0 (x >> s) | (x & (2**s - 1) != 0)。右移还是用 F T R F W r a p F B 2 A F Z e r o s
由于 F Z e r o s 2 s 0 F W r a p F W r a p F Z e r o s F W r a p & A l l 0 s F A N D F A N D
F R N T E l F R N T E x ≫ R r
c = g ∧ ( d ∨ f ) 我们首先用 TRS(x, r-2) 确认 f 1 x d , g , f F L U T c TR(x, 2) 并加上舍入结果 c
F R o u n d ∗ p , q , Q 给出浮点数 α = ( z , s , e , m ) ( e , m ) 已规格化的 尾数 m Q q m 1. M m = ( 1. M ) × 2 Q m [ 2 Q , 2 Q + 1 )
if 1{m >= 2^{Q+1} − 2^{Q−q−1}} then
Return (e+1, 2^q)
else
Return (e, m >>R (Q−q))
以下对该代码逻辑的正确性进行说明。尾数分为两种情况:
其一,当尾数的前 q q + 2 2 Q − q − 1 Q 2.0 e = e + 1 m q 2 q
其二,当不存在四舍五入后需要再次规范化的大多数情况,直接按照先前的 F R N T E Q − q
F F P A d d p , q 在前置知识一节,我们已经概括了普通浮点加法的办法。下面我们将该方法与伪代码对应:
指数对齐。若 E x E y x M x ← ( 1. M x ) 2 E x − E y , E ← E y
尾数相加。考虑S x , S y M = M x + M y M = | M x − M y | S
这里考虑同号与异号的情况。同号时,β 1 β 2 0 1 β 1 . s ⊕ β 2 . s = 1 m 2
规范化。这里我们找到加法结果 m q m 1 , m 2 2 q + 2 2 q + 1 k 1 2 q + 1 2 q + 1 − k K = 2 2 q + 1 − k
至于指数位的计算,由于先左移了 2 q + 1 − k q + 1 e = e − ( 2 q + 1 − k ) + ( q + 1 ) = e + k − q
写入结果。最后做一轮 F R o u n d ∗ p , q , 2 q + 1 | m 1 | > | m 2 | β 1 . s
F F P M u l p , q
符号位异或。S = S x ⊕ S y
指数相加。E = E x + E y − b i a s b i a s = 0
尾数相乘。M = M x ⋅ M y [ 2 2 q , 2 2 q + 2 )
规范化。如果结果 ≥ 2 2 q + 1 E M M
结果 ≥ 2 2 q + 1
在 M = M x ⋅ M y M F R N T E l
Math Functions
在《学数学,就这么简单》这本书中,有这样一个桥段:
F F P sin π 8 , 23 基于这样的思路,我们实际上可以细化出计算机是如何计算 sin x
首先利用三角函数诱导公式,将 x [ 0 , π / 2 ]
这是论文的做法,但实际上舍入到 [ − π / 4 , π / 4 ]
使用泰勒展开进行近似,例如 sin x ≈ x − 1 6 x 3 + 1 120 x 5
使用秦九韶算法 x − 1 6 x 3 + 1 120 x 5 = ( ( 1 120 x 2 − 1 6 ) x 2 + 1 ) x
这些运算就只需要浮点加法和乘法可以搞定,至于多项式的系数由于相对固定,可以通过查表解决。
我们现在对应到具体的原语 F F P sin π 8 , 23 sin π x
首先处理特殊情况:当 | x | > 2 23 q = 23 x sin π x = 0 | x | < 2 − 14 sin π x ≈ π x x
range reduction 步骤:目的是从输入 α a ∈ { 0 , 1 } δ | α | = 2 K + a + n n < 0.5 δ = n δ = 1 − n sin π α = ( − 1 ) a ⊕ 1 { α < 0 } sin π δ
m = α.m * 2^{α.e + 14}
a = TR(m, q+14); n = m mod 2^{q+14}
将 α | α | = 2 α . e ⋅ α . m 2 q m = α . m ⋅ 2 α . e + 14 ≈ | α | ⋅ 2 q + 14 a | α | n | α |
f = (n > 2^{q+13} ? 2^{q+14} - n : n)
k,K = MSNZB(f); f = f * K
z = 1{f=0}; e = (z ? -2^{p-1}+1 : k - q - 14)
第一行保证 f = δ ⋅ 2 q + 14 f f e
当 f = 0 sin π α = 0 z 1 e − 2 p − 1 + 1
δ = (z, 0, e, TR(f, q+14−Q))
最后重新将定点数 f Q δ
polynomial evaluation 步骤,注意论文使用了 Remez 等精度更高的逼近方法,而不是泰勒展开:
if 1{δ.e < −14} then
µ = Float_{p,Q}(π) ⊗_{p,Q} δ
先前 | δ | ≤ 2 − 14 sin π x ≈ π x
if 1{δ.e < −5} then
idx1 = δ.e + 14 mod 2^4
(θ1, θ3, θ5) = GetC_{4,9,5,p,Q}(idx1, Θ1_sin, K1_sin)
考虑 2 − 14 < | δ | < 2 − 5 K1_sin 这一常数类,在 Θ1_sin 这个表中,通过 index idx1(也就是 δ.e+14 的低4位)获取对应的参数 (θ1, θ3, θ5)。
4 是表的 bit 数,9 是 spline(系数对)的个数,5 是拟合的多项式的次数。
idx2 = 32 · (δ.e + 5 mod 27)
idx2 = idx2 + ZXt(TR(δ.m, Q−5) mod 32, 7)
idx2 = 1{δ.e = −1} ? 127 : idx2
(θ1, θ3, θ5) = GetC_{7,34,5,p,Q}(idx2, Θ2_sin, K2_sin)
在 2 − 5 ≤ | δ | < 0.5 δ.e + 5的低2位和δ.m的高5位进行查表的区分(这是论文的第二个创新点:分段索引 ),来调用对应误差最小的 (θ1, θ3, θ5)。对 | δ | = 0.5
使用秦九韶算法求出对应的浮点值:
Δ = δ ⊗_{p,Q} δ
µ = ((θ5 ⊗ Δ) ⊞* θ3) ⊗ Δ
µ = (µ ⊞* θ1) ⊗ δ
Return (µ.z, a ⊕ α.s, Round*(µ.e,µ.m))
Δ = δ 2
μ = ( θ 5 Δ + θ 3 ) Δ = θ 5 δ 4 + θ 3 δ 2
μ = ( μ + θ 1 ) δ = θ 5 δ 5 + θ 3 δ 3 + θ 1 δ ≈ sin π δ
前文说过:sin π α = ( − 1 ) a ⊕ 1 { α < 0 } sin π δ a ⊕ α.s 确定符号位,最后舍入即可得到最终结果。
大概总结一下,F F P sin π 8 , 23
这个方法一个潜在的缺点是,这个 GetC 函数用的表是 ad-hoc 的,与前面浮点四则运算的协议不同,如果想要任意指定p , q SecDouble ,这个系数表需要进行重新计算才能使得误差小于 1ULP。论文为了追求性能与准确度,牺牲了算法的灵活性。
F F P log 2 8 , 23 令 α = m ⋅ 2 N , m ∈ [ 1 , 2 ) , N = α . e a = 1 { N = − 1 }
N ≠ − 1 δ = m − 1 δ ∈ [ 0 , 1 ) log 2 α = log 2 m + N = log 2 ( 1 + δ ) + N N = − 1 m ≈ 2 log 2 m + N log 2 α = log 2 ( m / 2 ) = log 2 ( 1 − ( 1 − m / 2 ) ) δ ′ = 1 − m / 2 δ ′ ∈ ( 0 , 0.5 ] log 2 ( 1 − δ ′ )
log 2 ( α ) = { N + log 2 ( 1 + δ ) a = 0 , log 2 ( 1 − δ ′ ) a = 1. 然后,分别按照 a = 0 a = 1 ( θ 0 a , θ 1 a , θ 2 a , θ 3 a ) ( θ 0 b , θ 1 b , θ 2 b , θ 3 b ) δ . e δ . m
然后通过秦九韶算法(Horner's method)计算出 log 2 ( 1 + ⋅ ) N N F F P A d d p , q
range reduction 步骤:
a = 1{N = −1}
f = a ? (2^{q+1} − α.m) : (α.m − 2^q)
k,K = MSNZB(f); f = f *_{q+1} K
e = a ? (k − q − 1) : (k − q)
当 N = − 1 a = 1 f = 1 − m / 2 a = 0 f = m − 1 f
z = 1{f = 0}; e = (z ? −2^{p−1}+1 : e);
N = α.e; δ = (z,0,e, f *_{Q+1} 2^{Q−q})
通过 f δ q = 23 Q = 27
polynomial evaluation 步骤
if 1{δ.z} then
µ = Float_{p,Q}(0)
当 δ = 0 log 2 ( 1 + ⋅ ) = log 2 1 = 0 μ = 0
if 1{δ.e < −5} then
idx1 = (δ.e + 24) mod 2^5
(θa0,θa1,θa2,θa3) = GetC_{5,19,4,p,Q}(idx1, Θ1_log, K1_log)
(θb0,θb1,θb2,θb3) = GetC_{5,18,4,p,Q}(idx1, Θ3_log, K3_log)
当 2 − 24 ≤ δ < 2 − 5 δ.e + 24 的低5位作为 index,对 a = 1 Θ1_log,对 a = 0 Θ3_log,这里为了避免数据依赖必须两个都做。
else
idx2 = 16 · (δ.e + 5 mod 2^7)
idx2 = idx2 + ZXt(TR(δ.m, Q−4) mod 16, 7)
(θa0,θa1,θa2,θa3) = GetC_{7,20,4,p,Q}(idx2, Θ2_log, K2_log)
(θb0,θb1,θb2,θb3) = GetC_{7,32,4,p,Q}(idx2, Θ4_log, K4_log)
当 2 − 5 ≤ δ < 1 δ.e + 5 的低3位与 δ.m 的高4位作为 index,对 a = 1 Θ2_log,对 a = 0 Θ4_log。
(θ0,θ1,θ2,θ3) = a ? (θa0,θa1,θa2,θa3) : (θb0,θb1,θb2,θb3)
根据前文对 a
秦九韶算法(Horner)步骤及最后加N
µ = ((θ3 ⊗ δ) ⊞* θ2) ⊗ δ
µ = ((µ ⊞* θ1) ⊗ δ) ⊞* θ0
计算出三次多项式 μ = θ 3 δ 3 + θ 2 δ 2 + θ 1 δ + θ 0 = log 2 ( 1 + ⋅ )
β = LInt2Float(N)
β′ = (β.z,β.s,β.e, β.m *_{Q+1} 2^{Q-6})
将 N N β Q β ′
γ = a ? µ : (µ ⊞* β′)
Return (γ.z, γ.s, Round*(γ.e, γ.m))
最后执行浮点加法:
若 a = 0 γ = μ + β ′ = log 2 ( 1 + ⋅ ) + N
若 a = 1 γ = μ = log 2 ( 1 − ⋅ )
最终对 γ