English
为什么椭圆曲线点加满足结合律
这篇文章介绍椭圆曲线点加结合律的证明,以及更强的 9-points theorem。另外,也会涉及到该定理的三种推论:pascal 定理、pappus 定理,以及圆锥曲线极点极线的配极原则。
初等证明
(定理一:) 对于一个非奇异的椭圆曲线E : y 2 = x 3 + A x + B P , Q , R O P + Q P , Q E x E
( P + Q ) + R = P + ( Q + R ) (证明一:) 我们尝试用相对初等的方法来证明。设 E P , Q , R ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) λ a b = y b − y a x b − x a
P + Q = ( λ 12 2 − x 1 − x 2 , − λ 12 ( ( λ 12 2 − x 1 − x 2 ) − x 1 ) − y 1 ) 记该点为 S ( x s , y s )
Q + R = ( λ 23 2 − x 2 − x 3 , − λ 23 ( ( λ 23 2 − x 2 − x 3 ) − x 2 ) − y 2 ) 记该点为 T ( x t , y t )
然后计算:
x ( P + Q ) + R = λ s 3 2 − x s − x 3 x P + ( Q + R ) = λ 1 t 2 − x 1 − x t 然后验证 x ( P + Q ) + R = x P + ( Q + R ) 0
# 1) Base polynomial ring and fraction field
R = PolynomialRing(QQ, ['A','B','x1','y1','x2','y2','x3','y3'], order='lex')
A,B,x1,y1,x2,y2,x3,y3 = R.gens()
K = R.fraction_field()
# 2) Addition formulas (x- and y-coordinate) using secant/slope; generic position
def xAdd(xa, ya, xb, yb):
lam_ab = (yb - ya)/(xb - xa)
return lam_ab**2 - xa - xb
def yAdd(xa, ya, xb, yb):
lam_ab = (yb - ya)/(xb - xa)
return -lam_ab*((lam_ab**2 - xa - xb) - xa) - ya
# 3) Lift symbols to fraction field
A,B,x1,y1,x2,y2,x3,y3 = [K(z) for z in (A,B,x1,y1,x2,y2,x3,y3)]
# 4) Build x((P+Q)+R) and x(P+(Q+R))
x12 = xAdd(x1,y1,x2,y2); y12 = yAdd(x1,y1,x2,y2)
x23 = xAdd(x2,y2,x3,y3); y23 = yAdd(x2,y2,x3,y3)
xA = xAdd(x12,y12,x3,y3) # x((P+Q)+R)
xB = xAdd(x1,y1,x23,y23) # x(P+(Q+R))
# 5) Take common-denominator numerator and reduce modulo the curve ideal
diff = xA - xB
num = diff.numerator() # element of R up to a unit; denominators assumed nonzero (generic position)
I = R.ideal([
y1**2 - (x1**3 + A*x1 + B),
y2**2 - (x2**3 + A*x2 + B),
y3**2 - (x3**3 + A*x3 + B)
])
rem = I.reduce(num) # Gröbner normal form modulo the curve ideal
print(rem.is_zero())
程序输出 True,代表椭圆曲线上的点加结合律成立。
9-points theorem
事实上,这个结论不仅在椭圆曲线上成立,对于一般的三次曲线,也有这样的结论:
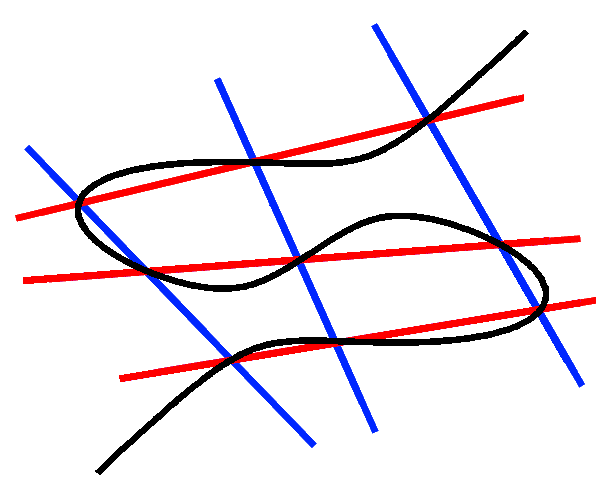
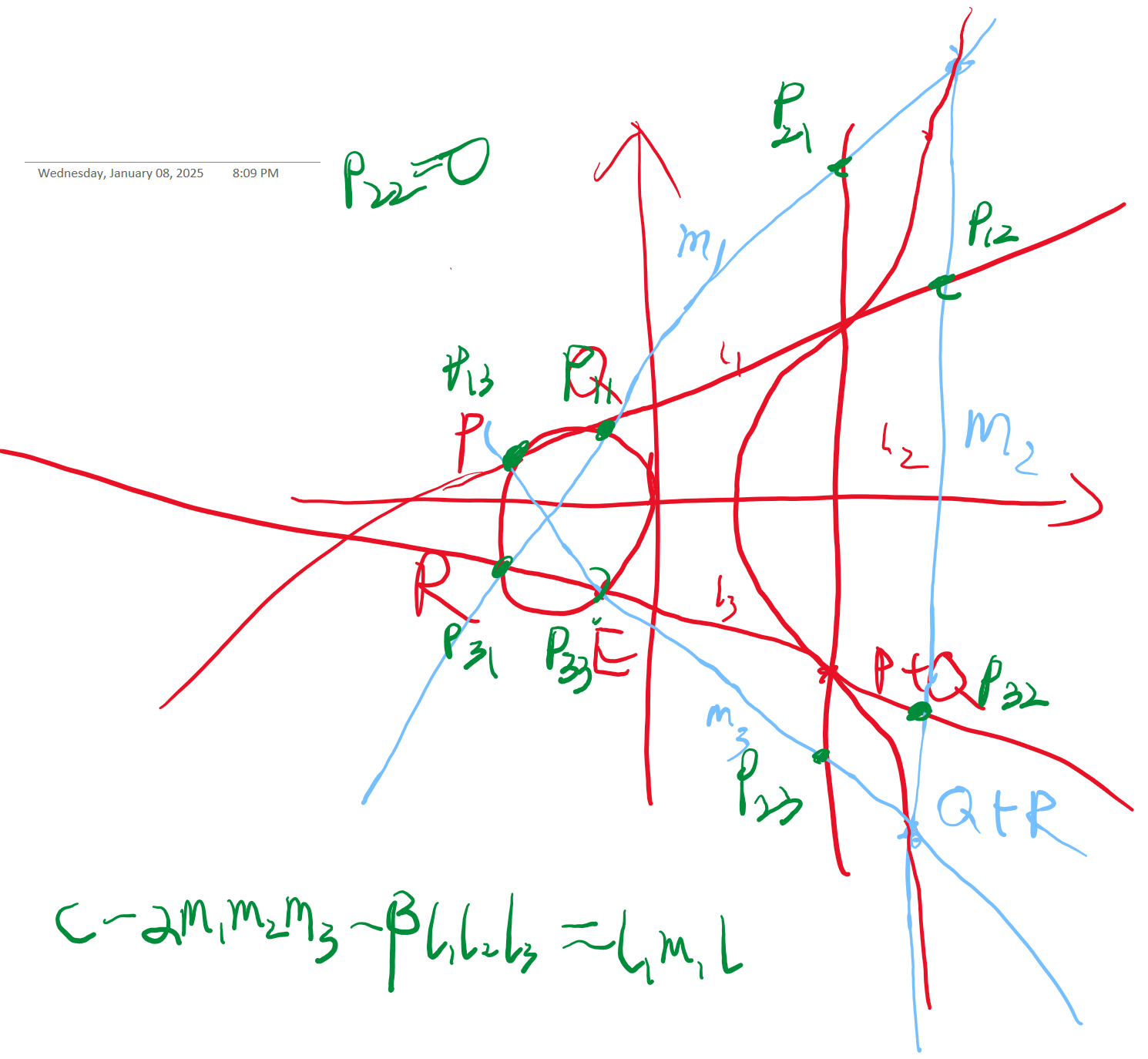
(定理二:) 在二次投影平面 P K 2 K C ( x , y , z ) = 0 C l 1 , l 2 , l 3 m 1 , m 2 , m 3 l i ≠ m j P i j = l i ∩ m j P 33 C P 33 C
一个直观的例子如下,这里的l 1 , 2 , 3 m 1 , 2 , 3 C
(证明二:) 证明的思路大致是令 D = C − α m 1 m 2 m 3 − β l 1 l 2 l 3 = 0 C = α m 1 m 2 m 3 + β l 1 l 2 l 3 P 33 l 3 m 3 α m 1 m 2 m 3 β l 1 l 2 l 3 0 C ( P 33 ) = 0 P 33 C
首先,我们尝试将直线方程 l ( x , y , z ) l P K 2 a x + b y + c z = 0
{ x = a 1 u + b 1 v y = a 2 u + b 2 v z = a 3 u + b 3 v 将直线的方程从 l ( x , y , z ) l ~ ( u , v ) l 1 P 11 , P 12 , P 13 ( u 1 , v 1 ) , ( u 2 , v 2 ) , ( u 3 , v 3 ) l 1 ( u , v ) l 1 m j m ~ j ( u , v ) P 11 , P 12 , P 13 m 1 , m 2 , m 3 m ~ j ( u j , v j ) = 0 P 1 j m j m ~ j ( u , v ) m ~ 1 ( u , v ) m ~ 2 ( u , v ) m ~ 3 ( u , v ) u , v
考虑以下引理:
(引理2.1:) 对于齐次三次多项式 R , S α R = α S
引理的理解非常直观,从单变量函数的角度来看,例如如果两个三次函数R S y = 0 x 1 , x 2 , x 3 ( x − x 1 ) ( x − x 2 ) ( x − x 3 ) R S α
对于另一个三次齐次多项式C l 1 C ~ ( u , v ) C ~ P 11 , P 12 , P 13 α C ~ = α m ~ 1 m ~ 2 m ~ 3
设 l 1 a x + b y + c z = 0 a , b , c a ≠ 0
{ x = − ( b / a ) u − ( c / a ) v y = u z = v 令C 1 = C − α m 1 m 2 m 3 C 1 ( l 1 ) = 0 C 1 x C 1 ( x , y , z ) = a 3 ( y , z ) x 3 + a 2 ( y , z ) x 2 + a 1 ( y , z ) x + a 0 ( y , z )
x n = ( 1 / a ) n ( ( a x + b y + c z ) − ( b y + c z ) ) n 因此可以变形为:
C 1 ( x , y , z ) = a 3 ′ ( y , z ) ( a x + b y + c z ) 3 + ⋯ + a 0 ′ ( y , z ) = a 0 ′ ( y , z ) 而 C ~ 1 ( u , v ) = C 1 ( − ( b / a ) u − ( c / a ) v , u , v ) = a 0 ′ ( u , v ) = 0 C 1 ( l 1 ) ≡ 0 a 0 ′ ( u , v ) = a 0 ′ ( y , z ) ( a x + b y + c z ) | ( C ( x , y , z ) − α m 1 m 2 m 3 )
l 1 | ( C − α m 1 m 2 m 3 ) 同理我们有:
m 1 | ( C − β l 1 l 2 l 3 ) 现在我们令:
D = C − α m 1 m 2 m 3 − β l 1 l 2 l 3 易证 m 1 | D , l 1 | D l 1 , m 1 gcd ( m 1 , l 1 ) = 1 m 1 l 1 | D D = l 1 m 1 l l
另外,我们由题设条件,C ( P 22 ) = C ( P 23 ) = C ( P 32 ) = 0 α m 1 m 2 m 3 + β l 1 l 2 l 3 0 D ( P 22 ) = D ( P 23 ) = D ( P 32 ) = 0 l 1 m 1 l ( P 22 ) = l ( P 23 ) = l ( P 32 ) = 0
注意到两点确定一条直线,这意味着 l l 2 m 2 l 2 ≠ m 2 l ≡ 0 D ≡ 0 C = α m 1 m 2 m 3 + β l 1 l 2 l 3 P 33 C
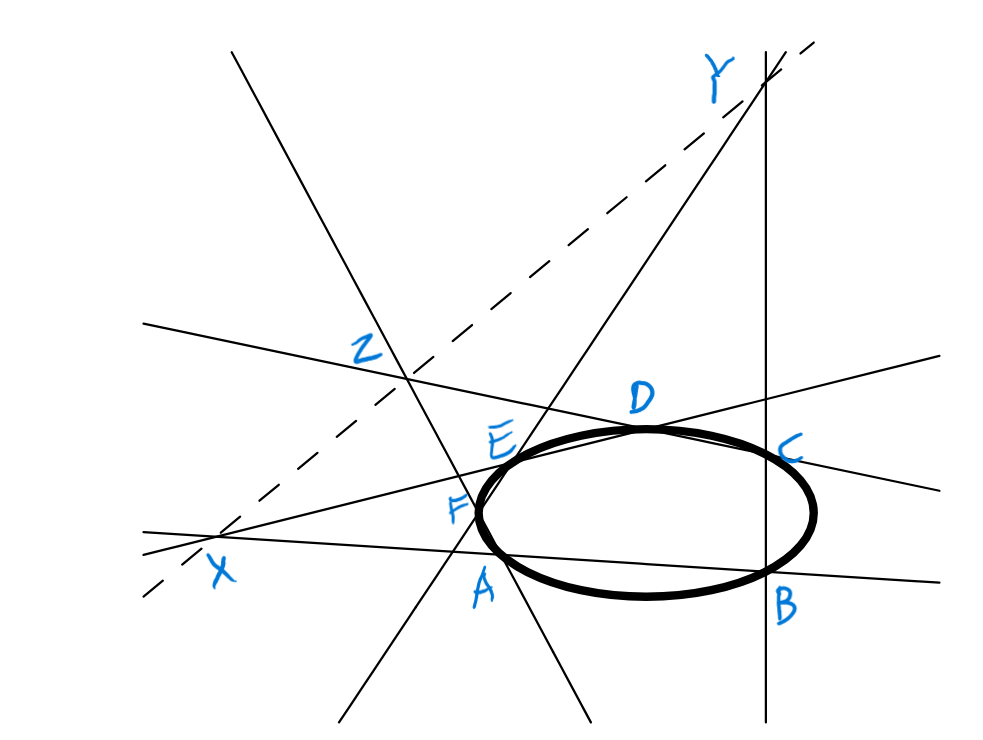
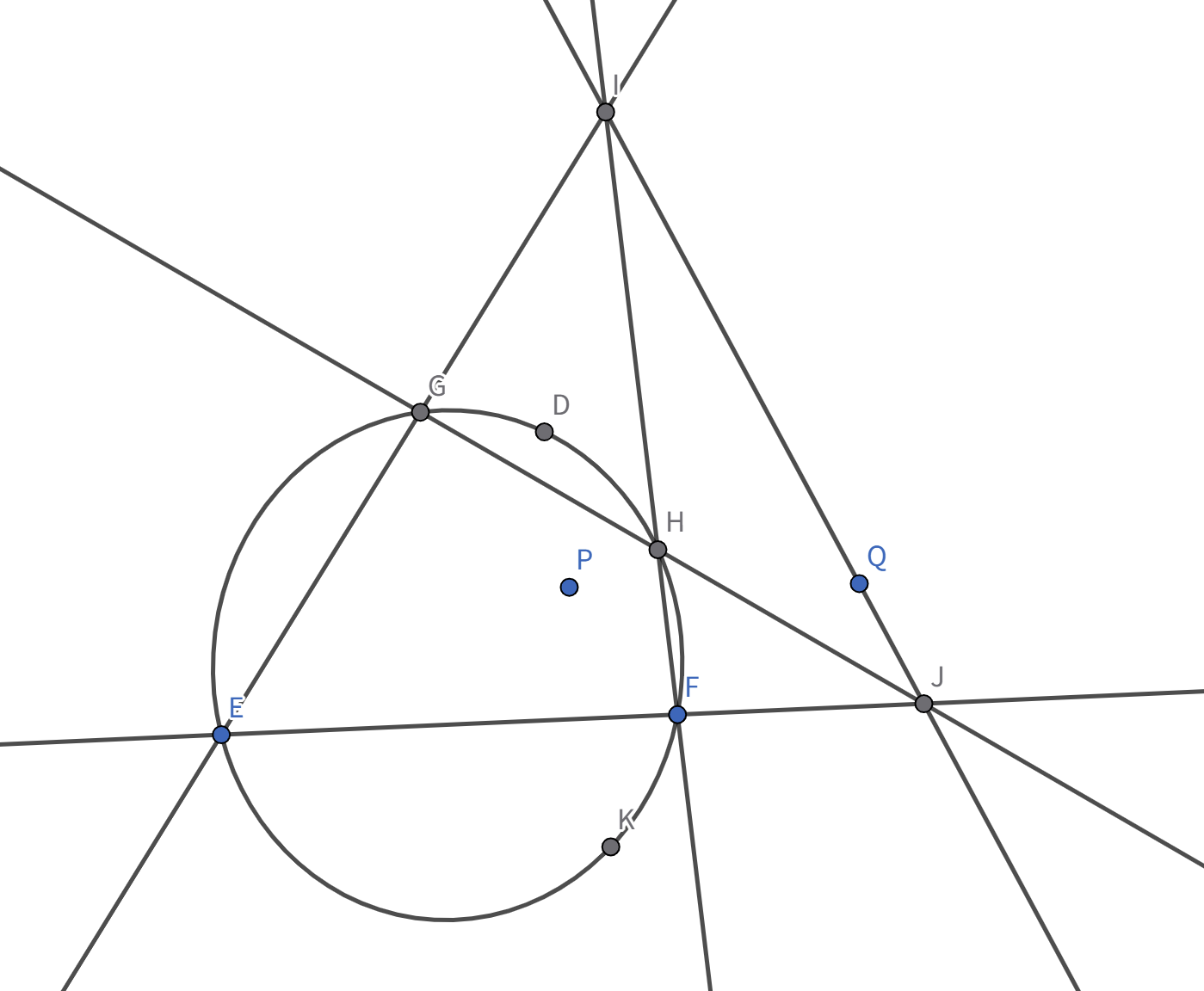
证明完 9-points theorem 后,我们便可以说明椭圆曲线的加法满足结合律。如下图所示,我们令点 P = P 13 , Q = P 11 , R = P 31 E − ( P + Q + R ) l 3 , m 3 C , l 3 , m 3 − ( ( P + Q ) + R ) l 3 , C − ( P + ( Q + R ) ) m 3 , C − ( ( P + Q ) + R ) = − ( P + ( Q + R ) )
9-points theorem 还有一个更一般的情况,具体如下:
(定理三, Cayley–Bacharach:) 设 X , Y ⊂ P 2 p 0 , p 1 , ⋯ , p 8 Z ⊂ P 2 p 1 , ⋯ , p 8 p 0
容易看到,X , Y
(证明三:) 这是一个代数几何的经典结论,你可以在 Hartshorne 的 GTM52 中(第 400 页,推论 4.5)看到。另外也可见香蕉空间的链接 。
Pascal/Pappus
(推论四, Pascal:) 设 A B C D E F Γ A , B , C , D , E , F X A B ― D E ― Y B C ― E F ― Z C D ― F A ― X , Y , Z
(证明四:) 令 l 1 = E F ― , l 2 = A B ― , l 3 = C D ― , m 1 = B C ― , m 2 = D E ― , m 3 = F A ― l m
l 1 l 2 l 3
m 1 Y B C
m 2 E X D
m 3 F A Z
我们令 Q ( x , y , z ) = 0 Γ l ( x , y , z ) = 0 X Y ―
C ( x , y , z ) = Q ( x , y , z ) l ( x , y , z ) 为一个齐次三次多项式,而 C = 0 A , B , C , D , E , F , X , Y P 2 C ( Z ) = 0 Q ( Z ) ≠ 0 l ( Z ) = 0 X , Y , Z
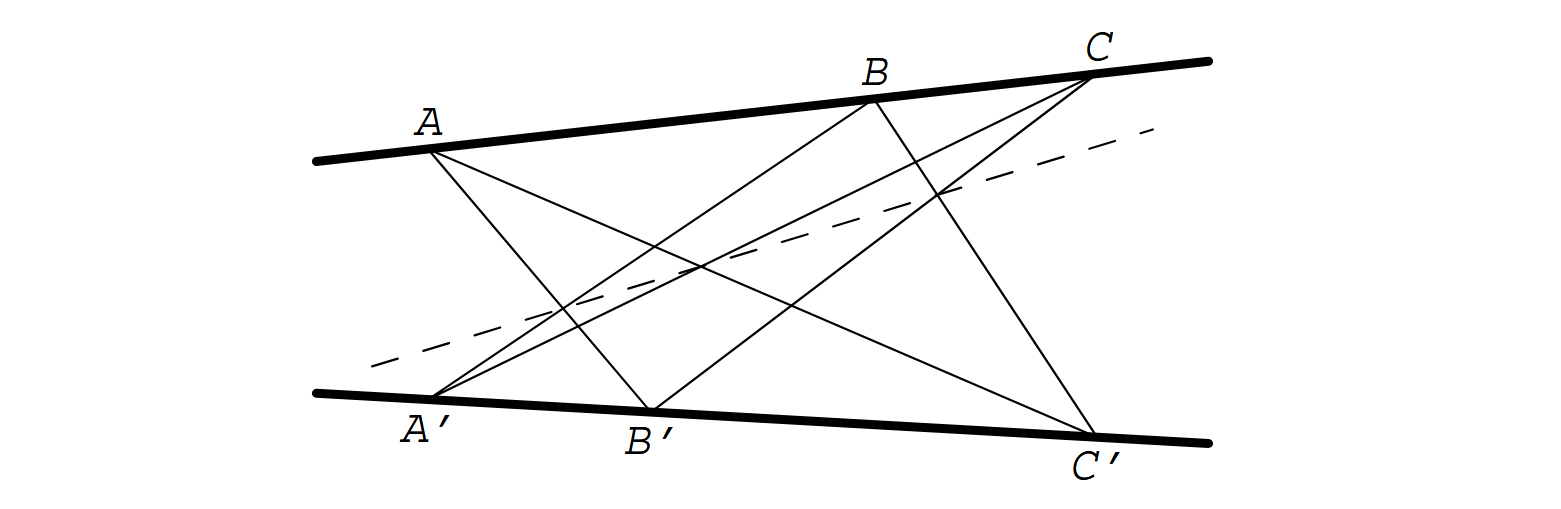
(推论五, Puppus:) 设 l m A , B , C l A ′ , B ′ , C ′ m l m X A B ′ ― A ′ B ― Y B ′ C ― B C ′ ― Z C A ′ ― C ′ A ― X , Y , Z
(证明五:) 这里l , m A B ′ C A ′ B C ′
极点与极线
当知道在椭圆上的 pascal 定理后,回想起高中有同学科普圆锥曲线的极点极线相关的性质,觉得这两个应该可以关联起来。这里首先引出极点极线的定义(这里以椭圆为例):
(定义六,极点极线:)
若点 P P A , B C , D A C B D S A D B C T P S T
若点 P P P
若点 P P
而极点与极线一个最基本的性质就是配极原则,其叙述如下:
(推论七,配极原则:) 对于同一椭圆,如果点P Q Q P
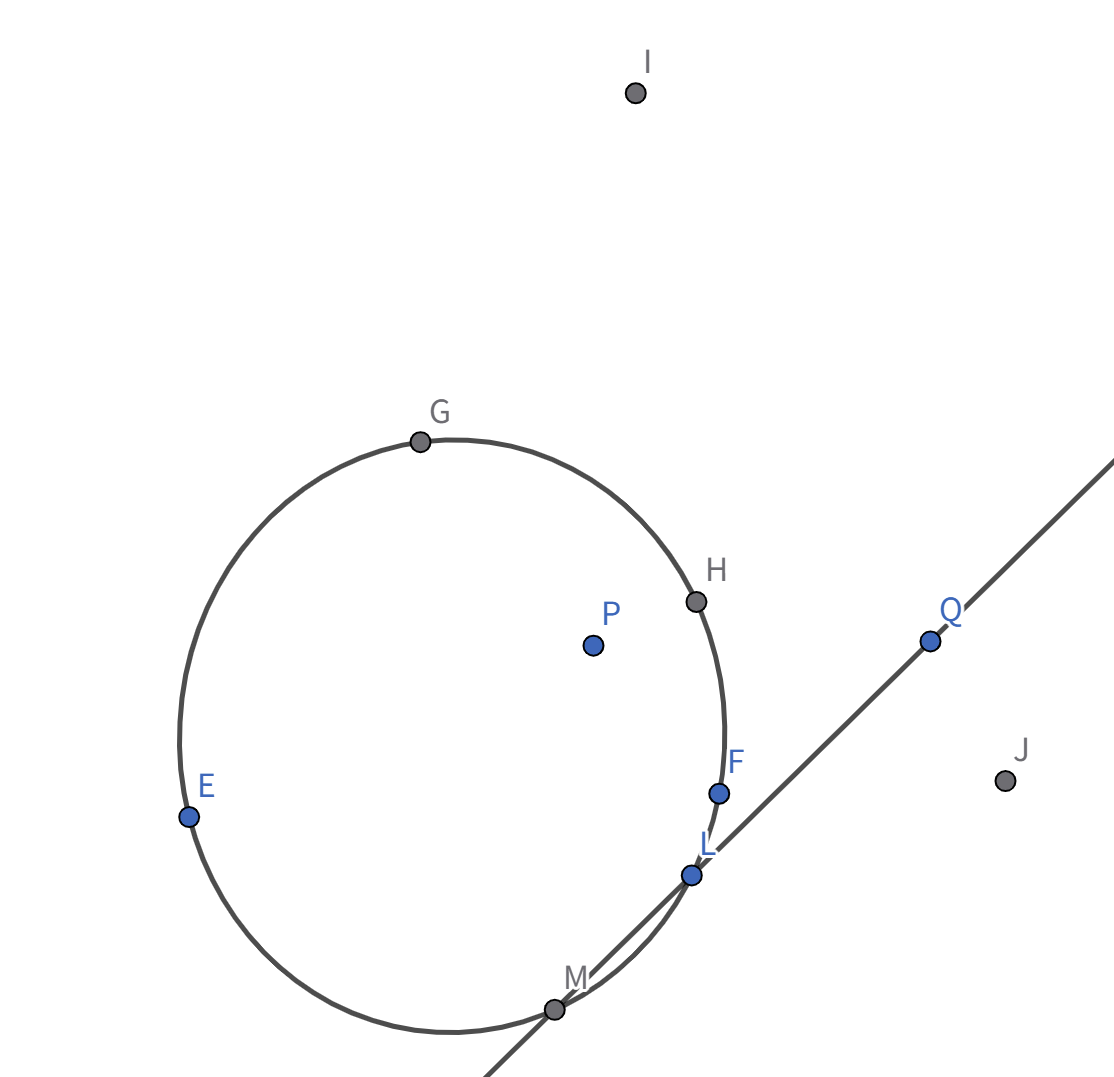
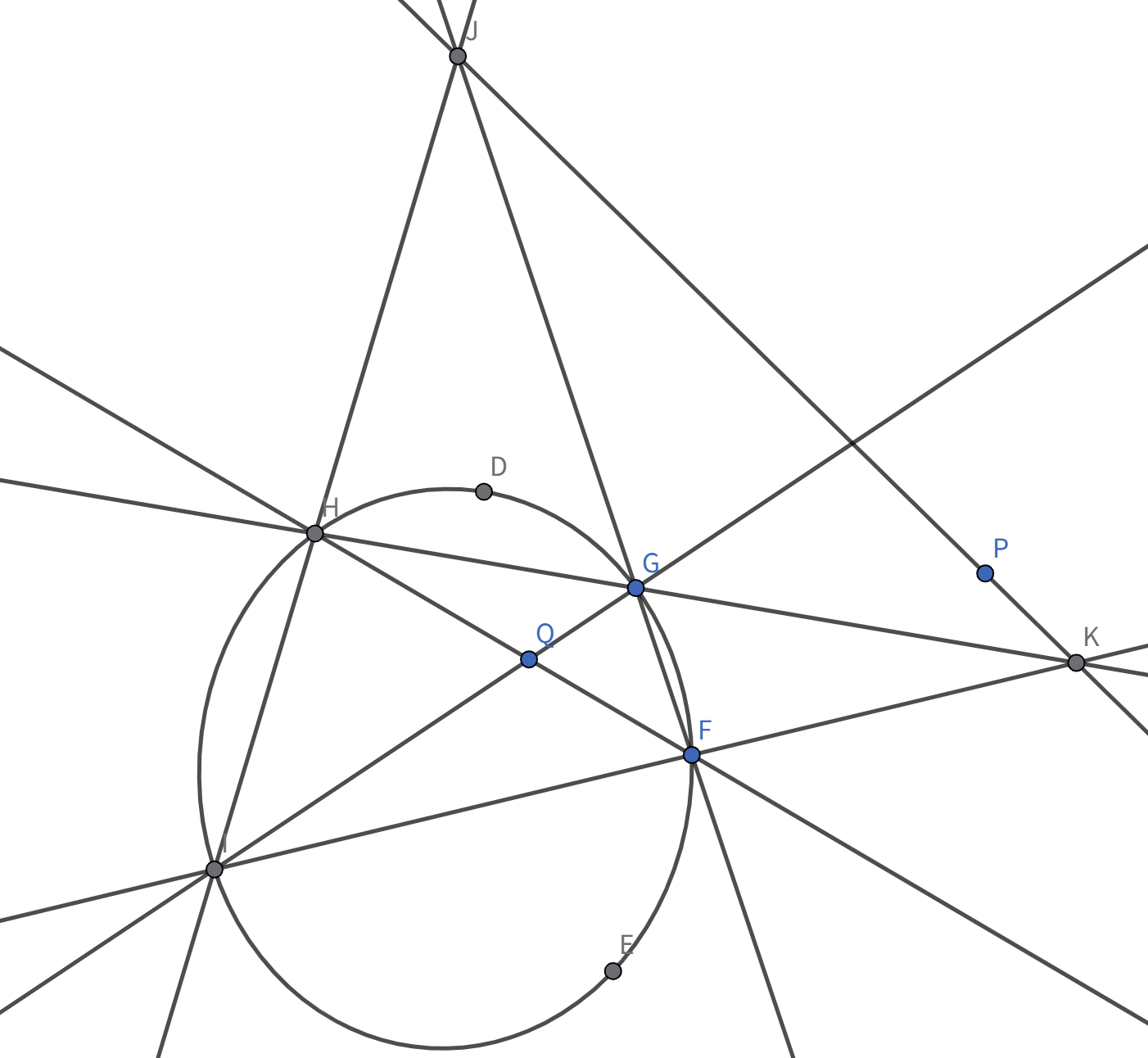
(证明七:) 这里提供一个仅使用 pascal 定理的纯几何证法。先考虑 P P I J
原证明便转化为:要证点 Q D , K D , P , K Q Q L
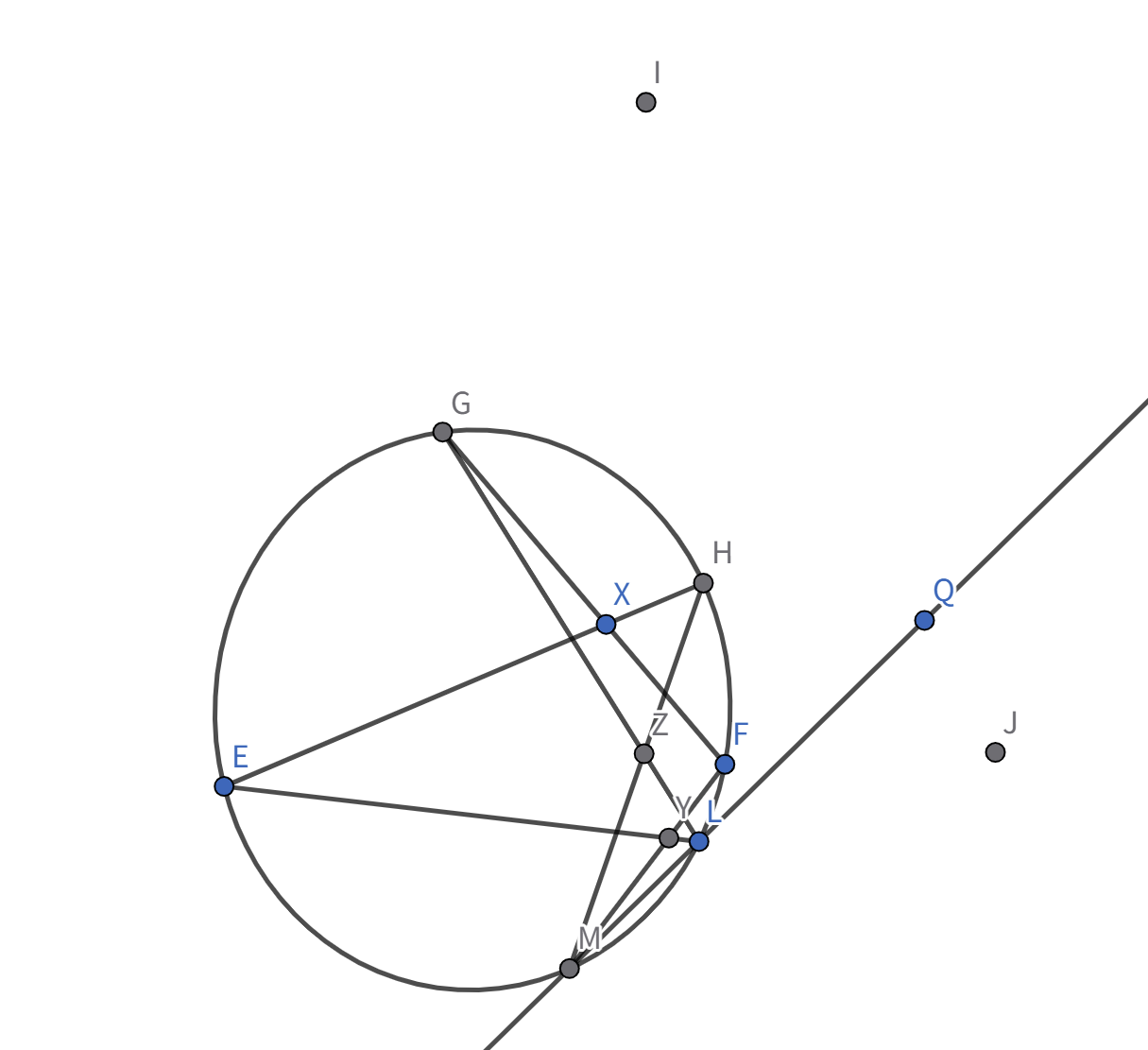
我们可以看到,H E L G F M H E ― , G F ― E L ― , F M ― L G ― , M H ― X , Y , Z
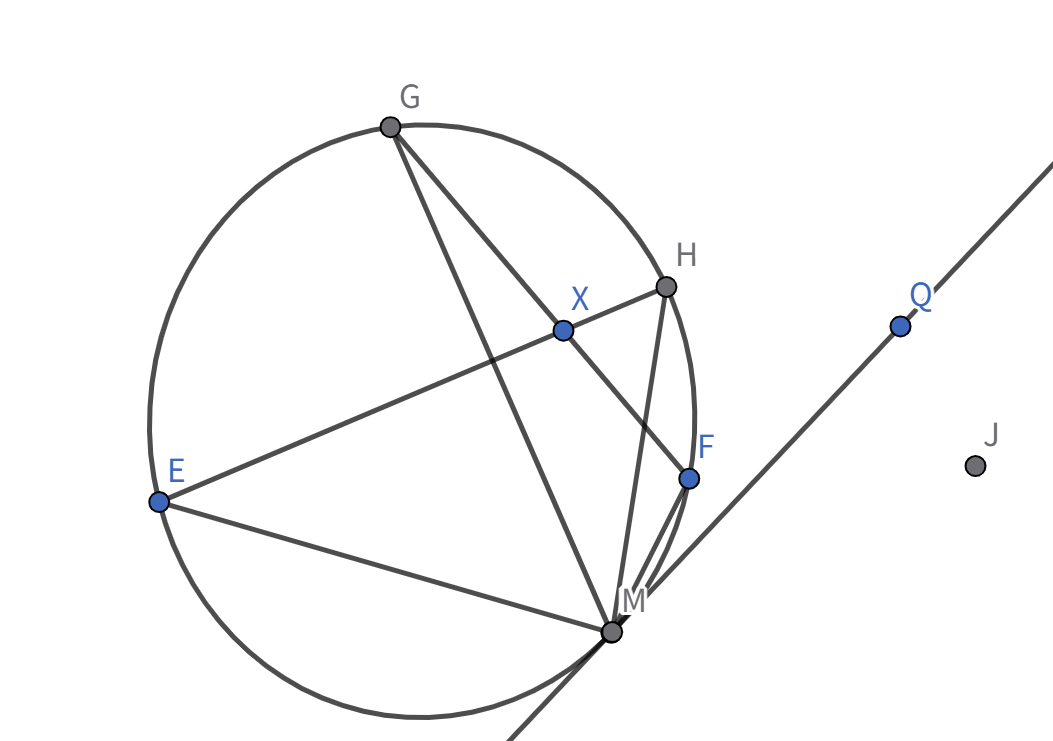
显然,这里的点 X P P Y Z Q L L , M Q L Y , Z L
因此我们可以得到结论,直线 P Y Z L Q L ′ L L ′ Q L L ′ P Y Z P Q
P P P Q Q P P
现在我们考虑 P P D , E P D E D E Q Q J K J , P , K
考虑椭圆内接六边形的退化情形 H H G F F I H G F I K G F I H J H F X J , X , K X Q J K
现在我们考虑将直线 H F Q D E Q J K D E X P P J K J , P , K
参考资料
Elliptic Curves: Number Theory and Cryptography
https://www.bananaspace.org/wiki/Cayley–Bacharach_定理
https://en.wikipedia.org/wiki/Cayley–Bacharach_theorem