（已完结）应用密码学笔记

简称为“大网安数”。

密码学概述

现代密码学四性：机密性，完整性，鉴别和不可抵赖性。

三个时期为：古典密码（算法保密），近代密码（密钥保密）和现代密码时期。

对密码系统的攻击：唯密文攻击，已知明文攻击，选择明文攻击，选择密文攻击。

Kerckhoffs原则：安全性只取决于密钥的保密，而不是算法。否则是“受限制的密码算法”。

安全性分类：无条件安全性，计算安全性，可证明安全性。

密码算法的功能：加密，杂凑，数字签名，身份鉴别，密钥协商。

私钥用于签名，公钥用于验证。

作业（p14）：

1-1，1-2，1-4，1-6，1-7

古典密码

单表替代密码

Caesar

$c = m + k$

$m = c - k$

仿射密码

$k = (k_{1}, k_{2})$

$c = k_{1} m + k_{2}$

$m = (c - k_{2}) k_{1}^{- 1} (\mod 26)$

密钥短语密码

把密钥放在最前面，剩余字母排在密钥后作为替换表。

缺点

词频分析。

多表替代密码

Vigenere

$c_{i} = m_{i} + k_{i}$

$m_{i} = c_{i} - k_{i}$

Hill

$C = K \cdot M$

$M = K^{- 1} \cdot C (\mod 26)$

其中 $C$ 与 $M$ 为列向量， $K_{n}$ 为加密矩阵。

优缺点：

对抗唯密文攻击，密钥空间大。
易受已知明文攻击与选择明文攻击。

OTP (Vernam)

$c_{i} = m_{i} \oplus k_{i}$

$m_{i} = c_{i} \oplus k_{i}$

不能重复使用密钥，理论上不可破译。

playfair

密钥字母去重，放在前面，剩下字母接上，i/j 一起占一个空，排成5*5的矩阵。

对明文两两分组（记为p1 p2），如果：

如果在同一行，那么密文就是明文靠右的字母。（最右的右边就是左边第一个）
如果在同一列，那么密文就是明文靠下的字母。（同理）
如果都不是，那么取另一个对角线作为密文，原文与对应密文的行相同。
如果相同（或剩一个），则在中间（右边）插一个约定的字母x。

链式密码算法

利用一个明文加密的结果作为下一个明文加密密钥。

缺点：误码扩散。

置换密码

周期置换

密钥规定了位置的置换。

属于Hill的特例，即属于线性变换的密码。

列置换密码

把明文按行填入矩阵，密钥规定以列读取的顺序。

转轮机密码

不考。

作业：

2.1 2.4 2.5 2.7 2.8 2.10 2.11 2.13 2.14 2.15

分组密码

设计原则

扩散原则：明文每一位影响密文尽可能多的位，密文每一位被尽可能多的明文影响。
混乱原则：敌手获得明文和密文也无法求出密钥的任意信息。
软件设计：使用子块和简单的运算。
硬件实现：尽量使用规则的结构。

若 $S^{2} = S$ 则是幂等密码体制，如仿射密码、置换密码等。

迭代密码体制必须是非幂等的。

典型结构

SPN结构：扩散更快速，但是加密和解密不相似。
Feistel结构：加密解密相似，扩散慢一些（至少需要两轮才能改变输入的每一位）。

$L_{i + 1} = R_{i}$

$R_{i + 1} = L_{i} \oplus F (R_{i}, K_{i})$

DES（重点）

安全性完全依赖于密钥保密。
密钥长度 64 位（8 位用于奇偶校验）

步骤：

明文IP置换。
$R_{0}$ 的 $E$ 扩展得到 $R_{0} (32 \to 48)$ ：把 $R_{0}$ 分成 $8$ 块，每块记为 $B_{1}$ 到 $B_{4}$ ，然后 $B_{1}$ 前面加上前一块的 $B_{4}$ ， $B_{4}$ 后面加上后一块的 $B_{1}$ .
对 $K_{0}$ 加上校验位（8的倍数），通过 $PC-1$ 得到C[0]和D[0]，左移一位得到C[1]和D[1]，通过PC-2得到 $48$ 位 $K_{1}$ .
$R_{0} \oplus K_{1}$
$S$ 盒变换 $(48 \to 32)$ ：不同的块是不同的 $S$ 盒，取 $B_{2}$ 到 $B_{5}$ 作为 $S$ 盒的行， $B_{1} B_{6}$ 作为 $S$ 盒的列（大端序），查表得到的值作为密钥块。（重点）
$P$ 盒变换。
与 $L_{0}$ 异或以后得到 $R_{1}$ ，便完成了一轮迭代。
经过 16 次迭代后再经过一次IP逆置换。

优点：

加密解密结构相同。
强度高。

互补对称性证明：

对于 $F$ 函数，有 $F (k, R) = P S (k \oplus E (R)) = P S (\overset{―}{k} \oplus E (\overset{―}{R})) = F (\overset{―}{k}, \overset{―}{R})$

从而轮函数 $Q_{k} (L, R) = (R, L \oplus F (k, R)) = (R, L \oplus F (\overset{―}{k}, \overset{―}{R}))$ ，进而 $\overset{―}{Q_{k} (L, R)} = (\overset{―}{R}, \overset{―}{L} \oplus F (\overset{―}{k}, \overset{―}{R})) = Q_{\overset{―}{k}} (\overset{―}{L}, \overset{―}{R})$

设 $D$ 为左右块对换， $x = (L, R)$ ，从而加密函数 $E_{\overset{―}{k}} (\overset{―}{x}) = D \cdot Q_{k_{16}} Q_{k_{15}} . . . Q_{k_{1}} (\overset{―}{x}) = D \cdot \overset{―}{Q_{k_{16}} Q_{k_{15}} . . . Q_{k_{1}} (x)} = \overset{―}{D \cdot Q_{k_{16}} Q_{k_{15}} . . . Q_{k_{1}} (x)} = \overset{―}{E_{k} (x)}$

改进：三重DES。

分组密码的工作模式

ECB：每块明文加密成相应的密码块，最后不足64 bit的部分用随机串补全。（本身是一种大的单字母替换）
CBC（常用）：当前明文块在加密之前要与前面的密文块进行异或，需严格保密初始向量。
CFB：按比分组小得多的单位进行加密，密文依赖于前面所有明文。
OFB：在块内部进行反馈。（易受篡改）
CTR：可并行、预处理，可产生较好的伪随机数序列。

如何选择：

安全性
高效性
功能

AES（重点）

数学基础

有限域 $GF (2^{8})$ 的乘法：略。

x乘：由于 AES 选取的模数为 0x11b，即 $x^{8} + x^{4} + x^{3} + x + 1$ ，当乘数高位为0时，相当于左移；反之相当于左移并异或0x1b.

叉乘：指 $GF (2^{8})$ 中两个四次式相乘，模数为 $x^{4} + 1$ 。可以通过矩阵乘法简化过程，具体而言，对于多项式 $\overset{―}{a_{3} a_{2} a_{1} a_{0}}$ 与 $\overset{―}{b_{3} b_{2} b_{1} b_{0}}$ ，乘积 $\overset{―}{d_{3} d_{2} d_{1} d_{0}}$ 为：

[\begin{matrix} d_{0} \\ d_{1} \\ d_{2} \\ d_{3} \end{matrix}] = [\begin{matrix} a_{0} & a_{3} & a_{2} & a_{1} \\ a_{1} & a_{0} & a_{3} & a_{2} \\ a_{2} & a_{1} & a_{0} & a_{3} \\ a_{3} & a_{2} & a_{1} & a_{0} \end{matrix}] \cdot [\begin{matrix} b_{0} \\ b_{1} \\ b_{2} \\ b_{3} \end{matrix}]

其中项与项的点乘就是 $GF (2^{8})$ 的乘法（使用x乘），加法就是异或。

步骤

密钥128位。

字节代换：查表。
行移位：第 $i$ 行循环左移 $i$ 字节。
列混淆（重点）：对每一列进行叉乘， $\overset{―}{a_{3} a_{2} a_{1} a_{0}}$ 固定为3112H.
轮密钥加：按列与轮密钥进行异或。

总过程：

AddRoundKey()

for i from 1 to 9:
  SubBytes()
  ShiftRows()
  MixColumns()
  AddRoundKey()

SubBytes()
ShiftRows()
MixColumns()

其它对称加密

IDEA (分组64bit, 密钥长度128bit, 非feistel结构)
RC6 (分组128bit, 密钥长度128,192,256bit, feistel)
SM4 (分组128bit，密钥长度128bit, 非对称feistel)

非对称加密

对称的缺点

系统开放性差（如何传递密钥）
密钥管理困难， $n$ 个设备有 $\frac{n (n - 1)}{2}$ 个密钥。
数字签名问题。

公钥的特点

公钥管理方便，开放性好
加解密计算代价较大

公钥的作用

常规密钥分发与协商
数字签名
加密解密（效率较低且不宜直接使用）

RSA

具体过程：略

用CRT实现RSA的快速计算

例：计算 $m^{d} (\mod n)$ ，其中 $n = p q$ ， $p, q$ 为互异素数， $d$ 为密钥。

解：分别用欧拉定理计算 $m^{d} (\mod p)$ 和 $m^{d} (\mod q)$ 的值，然后用CRT计算 $m^{d} (\mod n)$ 即可。

Miller-Rabin

费马小定理是模数为素数的必要条件。

二次探测定理：若 $p$ 是奇素数，则 $x^{2} \equiv 1 (\mod p)$ 的解只有 $x \equiv 1$ 或 $x \equiv - 1$ .

伪代码：

# false rate: 1 - 4^(-s)
def WITNESS(a, n):
  if pow(a, n-1, n) != 1:
    return FALSE
  else while n % 2 == 0:
    n /= 2
    if pow(a, n-1, n) != 1 or -1:
      return FALSE
  return TRUE

for i from 1 to s:
  if WITNESS(integers[i], n) == FALSE
    return NOT_PRIME
return PRIME

ElGamal

description

系统参数： $p, α \in Z_{p}^{*}$ .

选取私钥 $x_{A}$ ，公钥为 $y_{A} = α^{x_{A}} (\mod p)$

加密：

选取随机数 $k \in [2, p - 2]$
$c_{1} = α^{k} (\mod p)$
$c_{2} = m \cdot y_{A}^{k} (\mod p)$

解密：

$m = c_{2} \cdot (c_{1}^{x_{A}})^{- 1} (\mod p)$

feature

非确定性的（依赖于k）
密文空间大于明文空间

ECC

SM2也使用了椭圆曲线密码体制

实数域上的椭圆曲线

$y^{2} = x^{3} + a x + b$ 可记为 $E (a, b)$ ，简称为 $E$

若 $P, Q, R$ 共线，则定义加法单位元 $O = P + Q + R$ ，对曲线上任意一点有 $P + O = P$

易得加法逆元与本身的 $y$ 轴互为相反数

因此可得加法的定义：做过 $P, Q$ 的直线交 $E$ 于 $R$ ，则 $- R$ 为 $P + Q$ ，由加法可以类比倍加的定义（此处省略）。可以证明，这种加法满足交换律和结合律。

从代数角度而言 $P + Q = (x_{3}, y_{3}) = (λ^{2} - x_{1} - x_{2}, λ (x_{1} - x_{3}) - y_{1})$ ， $λ$ 为直线斜率，若 $P, Q$ 重合则 $λ = \frac{3 x^{2} + a}{2 y}$

有限域上的椭圆曲线

重点 $GF (p)$ ， $GF (2^{n})$ 不考。

$y^{2} = x^{3} + a x + b (\mod p)$ 可记为 $E_{p} (a, b)$ ，简称为 $E_{p}$

可以证明，有限域上的椭圆曲线关于运算 + 构成循环群。

加法的定义把对应坐标模 $p$ 即可，倍加类似。

例：求 $E_{11} (1, 6)$ 中点的个数：

答：一共有13个（不要忘了 $O$ 点！）

椭圆曲线上的ElGamal

记 $ord (P)$ 为满足 $n P = O$ 的最小整数 $n$ .

ECDLP: 已知 $α, β$ ，求 $k α = β$ 的 $k \in [0, ord (α) - 1]$ 是困难的。

类似于离散对数(DLP)问题，可以把点加类比于模乘，倍加类比于方幂。

系统参数： $E (a, b)$ ，基点 $G$ （其阶为 $n$ ）。

密钥生成：选取私钥 $d_{A}$ ，公钥为 $P_{A} = d_{A} G$

加密：

将明文消息 $m$ 映射到点 $P_{m}$
选取随机数 $k \in [2, n - 1]$
$c_{1} = k G$
$c_{2} = P_{m} + k P_{A}$

解密：

$P_{m} = c_{2} - d_{A} c_{1}$
对 $P_{m}$ 逆映射得到 $m$

Menezes-Vanstone

主要解决将明文 $m$ 映射到 $P_{m}$ 的问题

系统参数： $E (a, b)$ ，基点 $G$ （其阶为 $n$ ）。

密钥生成：选取私钥 $d_{A}$ ，公钥为 $P_{A} = d_{A} G$

加密：

$m = (m_{1}, m_{2})$
选取随机数 $k \in [2, n - 1]$
$c_{1} = k G$
$Y = (y_{1}, y_{2}) = k P_{A}$
$c_{2} = y_{1} m_{1} (\mod p)$
$c_{3} = y_{2} m_{2} (\mod p)$

解密：

$d_{A} c_{1} = (z_{1}, z_{2})$ （注意到 $d_{A} c_{1} = k P_{A}$ ，故 $y_{1} = z_{1}, y_{2} = z_{2}$ ）
$m_{1} = c_{2} z_{1}^{- 1} (\mod p)$
$m_{2} = c_{3} z_{2}^{- 1} (\mod p)$
由 $(m_{1}, m_{2})$ 得到 $m$

例：设 $E_{11} (1, 6)$ 中基点 $G$ 为 $(2, 7)$ ，密钥 $d = 7$ ，明文为 $(9, 1)$ ，随机数 $k = 6$ ，计算密文。

解：计算公钥 $P_{A} = d G = 7 (2, 7) = (7, 2)$

$c_{1} = 6 G = (7, 9)$

$Y = k P_{A} = k d G = 42 G = 3 G = (8, 3)$

$c_{2} = 8 \times 9 = 6 (\mod p)$

$c_{3} = 3 \times 1 = 3 (\mod p)$

故密文为 $((7, 9), 6, 3)$

代码实现（晚上写作业时搞的）

# ECC en&decrypt in GF(p)
# 4/24/2023 junyu33
import gmpy2
a = 1
b = 6
p = 11
G = [2, 7]
d_A = 5
def Add(A: list, B: list) -> list:
    lamb = 0
    if A == B:
        lamb = (3*A[0]*A[0]+a)*gmpy2.invert(2*A[1], p) % p
    else:
        lamb = (B[1]-A[1])*gmpy2.invert(B[0]-A[0], p) % p
    s = (lamb**2 - A[0] - B[0]) % p
    t = (lamb*(A[0]-s) - A[1]) % p
    return [s,t]

def Mult(X: list, t: int) -> list:
    R = X
    t = t - 1
    while t:
        if t & 1:
            R = Add(R, X)
        X = Add(X, X)
        t >>= 1
    return R

def enc(M: list, G: list, k: int):
    c_1 = Mult(G, k)
    P_A = Mult(G, d_A)
    Y = Mult(P_A, k)
    c_2 = Y[0] * M[0] % p
    c_3 = Y[1] * M[1] % p
    print(c_1, c_2, c_3)

def dec(c_1: list, c_2: int, c_3: int):
    Y = Mult(c_1, d_A)
    z_1 = Y[0]
    z_2 = Y[1]
    m_1 = c_2 * gmpy2.invert(z_1, p) % p
    m_2 = c_3 * gmpy2.invert(z_2, p) % p
    print(m_1, m_2)

enc([7,9],G,3)

哈希

SHA-1（已被破解）

big-endian

2**64-1 -> 160 bit

steps

填充：origin + 1000...000(长度448-len%512) + len
初始MD缓存：A=67452301 B=EFCDAB89 C=98BADCFE D=10325476 E=C3D2E1F0
以512bit为一组处理信息：A,B,C,D,E←[(A<<5)+ft(B,C,D)+E+Wt+Kt],A,(B<<30),C,D，共80轮循环，这里：
- $f_{t}$ 是逻辑函数，分别为(b&c)|(b&d) b^c^d (b&c)|(b&d)|(c&d) b^c^d;
- $W_{t}$ 为子明文分组W[t]，每项32位，前16项就是原文512bit的对应，之后的项为(W[t-16]^W[t-14]^W[t-8]^W[t-3])<<1，共80项;
- $K_{t}$ 为固定常数（ $1 \leq t \leq 4$ ），分别为5A827999 6ED9EBA1 8F1BBCDC CA62C1D6
- 最开始20轮循环 $t$ 取1，然后20轮 $t$ 取2，以此类推。
将原先的A,B,C,D,E与最后得到的A',B',C',D',E'相加得到新一轮的缓存，处理完所有明文后得到的缓存就是SHA-1值。

生日攻击

如果消息空间的大小为 $N$ ，那么大概随机选择 $\sqrt{N}$ 个消息，就有一半的概率产生碰撞。

SM3

国内商用密码 Hash 函数。

分组 512 bit，输出 256 bit。

智能电表，TPM2.0

消息鉴别

消息鉴别码（Message Authentication Code, MAC）的分类：

加密技术
散列函数
HMAC算法（带密钥的单向散列函数）

数字签名

RSA

发送者使用 $s_{A} = m^{d} (\mod n)$ 进行签名。

接收者使用 $m = s_{A}^{e} (\mod n)$ 进行验证。

ElGamal

初始化： $e_{A} = α^{d_{A}} (\mod p)$

签名变换：

选取随机数 $k$ ，与 $p - 1$ 互素
签名：
- $r = α^{k} (\mod p)$
- $s = (H (M) - d_{A} r) k^{- 1} (\mod p - 1)$ ，其中 $H$ 为单向散列函数。
- 发送 $r, s$
验证：
- 计算 $H (M)$
- 计算 $e_{A}^{r} r^{s} (\mod p)$ 与 $α^{H (M)} (\mod p)$ ，若相等则签名有效。

注意 $k$ 不能被泄露，加密部分同理。

DSA

$p, q, g$ 公开， $q$ 是 $p - 1$ 的素因子， $g = h^{(p - 1) / q} (\mod p)$

随机选取 $x$ 作为私钥，公钥 $y = g^{x} (\mod p)$

签名变换：

签名：
- 选取 $k \in (0, q)$
- $r = (g^{k} (\mod p)) (\mod q)$
- $s = k^{- 1} (H (m) + x r) (\mod q)$
- 发送 $r, s$
验证：
- $w = s^{- 1} (\mod q)$
- $u_{1} = H (m) w (\mod q)$
- $u_{2} = r w (\mod q)$
- $v = (g^{u_{1}} y^{u_{2}} (\mod p)) (\mod q)$ ，若 $v = r$ 则签名成功。

ECDSA

$E (F_{p}), G, n$ 为系统参数。

随机选取 $d \in (1, n)$ 作为私钥， $Q = d G$ 作为公钥。

签名：
- 选择随机数 $k \in (1, n - 1)$
- $k G = (x_{1}, y_{1})$
- $r = x_{1} (\mod n)$
- $s = k^{- 1} (h (M) + d r) (\mod n)$
- 发送 $r, s$
验证：
- $u_{1} = h (M) s^{- 1} (\mod n)$
- $u_{2} = r s^{- 1} (\mod n)$
- $X (x_{2}, y_{2}) = u_{1} G + u_{2} Q$
- $v = x_{2} (\mod n)$ ，若 $v = r$ 则接受签名。

特殊签名

不可否认签名
盲数字签名
群签名

密钥管理技术

Diffie-Hellman (非对称，只能用于两个用户的密钥交换)

系统参数： $p, α$

Alice 选取不公开的 $r_{a}$ ，计算 $s_{a} = α^{r_{a}} (\mod p)$
Bob 选取不公开的 $r_{b}$ ，计算 $s_{b} = α^{r_{b}} (\mod p)$
双方交换 $s_{a}$ ， $s_{b}$
Alice 计算 $s_{b}^{r_{a}} (\mod p)$
Bob 计算 $s_{a}^{r_{b}} (\mod p)$

显然以上两个值相等，密钥协商完成。

易受中间人攻击。

Shamir 门限方案

系统参数： $k, n, q$

秘密： $s, a_{1}, a_{2}, \dots, a_{k - 1}$

因此可构造出秘密多项式：

f (x) = s + a_{1} x + a_{2} x^{2} + \dots + a_{k - 1} x^{k - 1}

密钥分发者根据每个人的密钥 $x_{i}$ 计算出 $f (x_{i})$ 的值，各自分发给他们。

由拉格朗日插值，只有任意取 $\geq k$ 个人才能还原出秘密多项式（重构），过程如下：

f (x) = \sum_{i = 1}^{k} f (x_{i}) \prod_{j = 1, j \neq i}^{k} \frac{x - x_{j}}{x_{i} - x_{j}} (\mod q)

特别的，当 $x = 0$ 时，可以计算出秘密 $s$ 的值：

s = f (0) = (- 1)^{k - 1} \sum_{i = 1}^{k} f (x_{i}) \prod_{j = 1, j \neq i}^{k} \frac{x_{j}}{x_{i} - x_{j}} (\mod q)

不足：

门限值固定
秘密分发者知道参与者的shadow
不能防止秘密分发者和参与者的欺诈

身份鉴别技术

概念，威胁，攻击手段

质询——响应身份鉴别：

额外通信代价
只能防止声称者的重放，不能防止验证者的重放攻击：双向鉴别、时间戳。

S/Key OTP 身份鉴别：

可防止重放攻击
不能防止小数攻击（截取服务器的种子和迭代值，修改较小迭代值发给用户，截获用户口令，计算较大迭代值）
缺乏完整性保护机制

零知识证明协议

设 $n = p \times q$ ，假设 Alice 知道 $n$ 的因子，如果 Alice 想告诉 Bob 她知道但不具体告诉 Bob 因子是什么，可以执行以下步骤：

Bob 随机选取 $x$ ，计算 $y = x^{4} (\mod n)$ ，并将 $y$ 告诉 Alice
Alice 计算 $z = \sqrt{y} (\mod n)$ ，并将 $z$ 告诉 Bob
Bob 验证 $z = x^{2} (\mod n)$ 是否成立。
重复多次都能成功就代表 Alice 确实知道 $n$ 的因子

理论基础是计算 $\sqrt{y} (\mod n)$ 的难度等价于对 $n$ 进行因式分解。

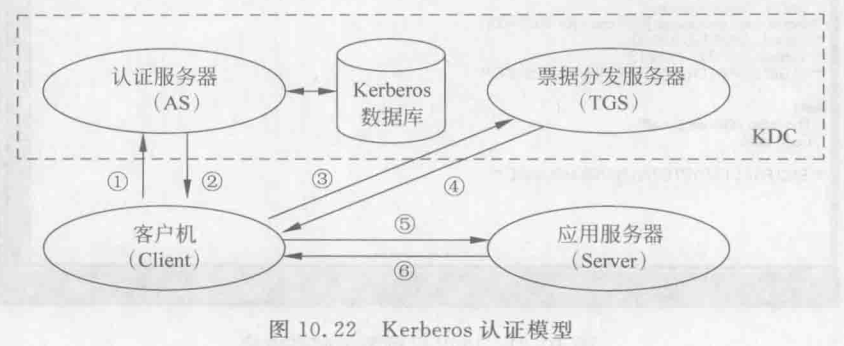
kerberos 身份鉴别

采用对称密钥体制，由可信第三方提供鉴别服务。

通过票据（ticket）给通信双方分发共享密钥。

安全通信

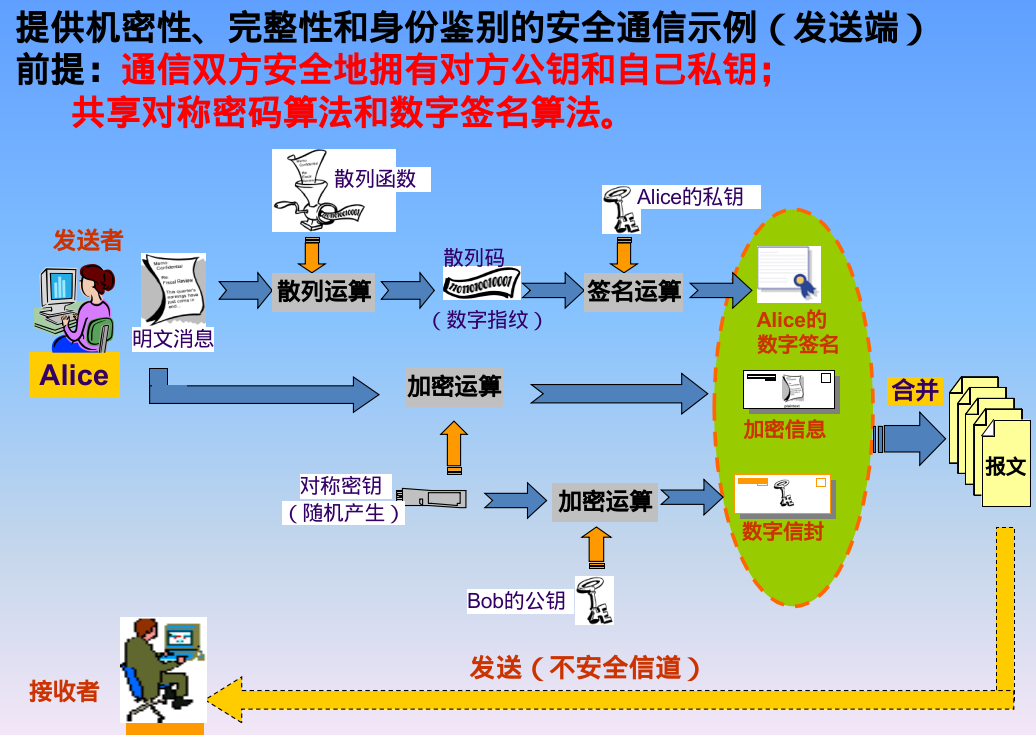
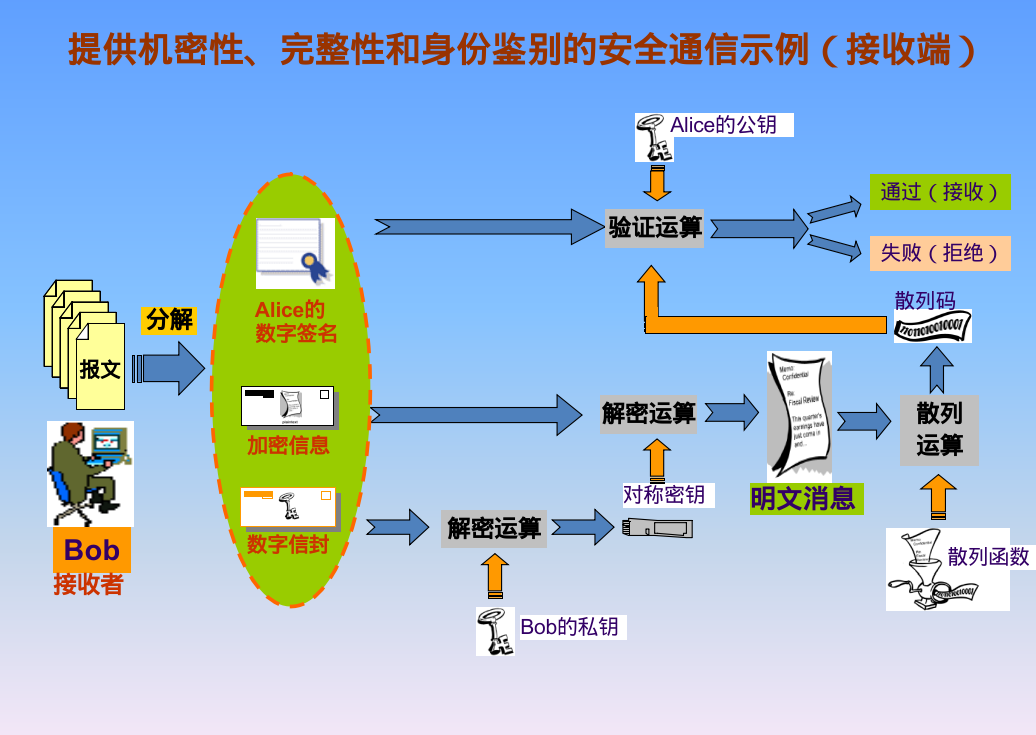
伪代码：

发送方：

# send.py
# Example usage:
with open("public_key_B.pem", "rb") as f:
  public_key_B = RSA.import_key(f.read())

with open('data', 'rb') as f:
  data = f.read()

# Party A encrypts the data and signs it
ciphertext = encrypt(data, key)
signature = sign(data, private_key_A)

# Party A encrypts the key using the public key of party B
encrypted_key = encrypt_key(key, public_key_B)

with open('encrypted_key', 'wb') as f:
  f.write(encrypted_key)

with open('ciphertext', 'wb') as f:
  f.write(ciphertext)

with open('signature', 'wb') as f:
  f.write(signature)

with open('public_key_A.pem', 'wb') as f:
  f.write(public_key_A.export_key('PEM'))

接收方

# receive.py
with open('public_key_A.pem', 'rb') as f:
  public_key_A = RSA.import_key(f.read())
with open('encrypted_key', 'rb') as f:
  encrypted_key = f.read()

with open('signature', 'rb') as f:
  signature = f.read()

with open('ciphertext', 'rb') as f:
  ciphertext = f.read()

# Party B decrypts the key and uses it to decrypt the data
key = decrypt_key(encrypted_key, private_key_B)
decrypted_data = decrypt(ciphertext, key)
with open('decrypted_data', 'wb') as f:
  f.write(decrypted_data)

# Party B verifies the signature of party A
is_valid = verify_signature(decrypted_data, signature, public_key_A)

if is_valid:
  print("The signature is valid")
else:
  print("The signature is not valid")

序列密码基础

又称流密码，属于对称密码体制，适合硬件实现。

LFSR

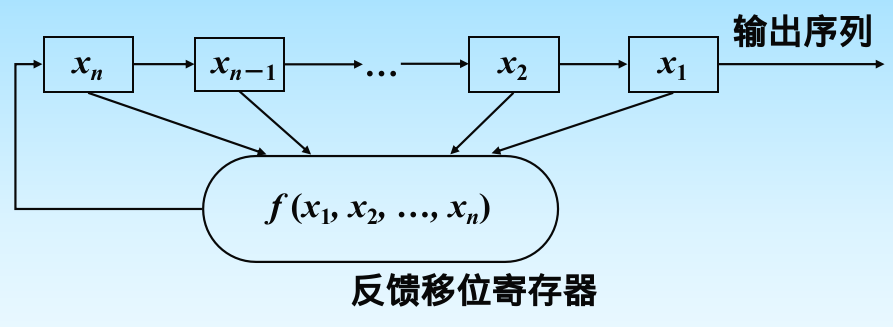
注意是高位移向低位， $x_{1}$ 就是输出， $f$ 的值为下一个 $x_{n}$ .

性质完全由反馈函数决定。 $n$ 级LFSR周期 $T \leq 2^{n} - 1$ .

基于LFSR的序列密码生成器有：

Geffe生成器
钟控生成器
交错停走式生成器

RC4

两个算法：密钥调度算法KSA、伪随机数生成算法PRGA。