题解 P5389 【[Cnoi2019]数学课】

样例是怎么算的

由于n=2时不容易看出规律，这里取n=3，看懂后类比即可。

首先我们对n=3打表，可以发现取1时概率为1/10，取3时概率为3/10，取6时概率为6/10.再由手动计算出每种情况获胜的概率后，得到这样一张图。

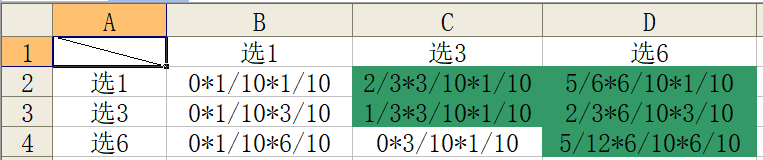
可以得出概率为2/5.

对于每种情况的概率可以 $O (1)$ 算出（过程自己想想），时间复杂度为 $O (n^{2})$ .

如何优化

我们直接考虑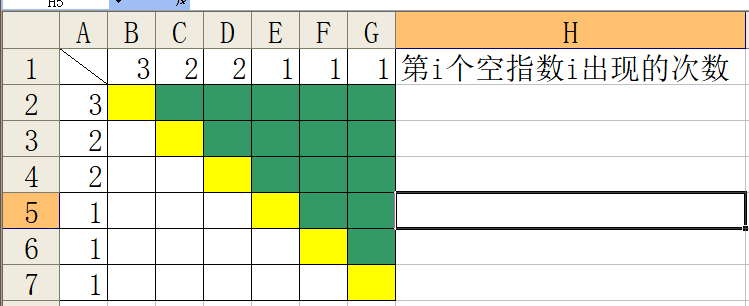 $a$ ， $b$ 在 $[1, a_{n}]$ 中的每个数出现的概率，由于取 $x$ 时概率的分子恰为 $x$ ，我们可以理解为在 $1 - x$ 中均出现一次。整理后如下图：我们可以发现我们只需用总的次数减掉黄色的次数，再除以2即可。

此时我们可以 $O (n)$ 解决这个问题。

推公式

黄色出现的次数是:

1^{2} * n + 2^{2} * (n - 1) + . . . + n^{2} * 1

= 1^{2} + (1^{2} + 2^{2}) + (1^{2} + 2^{2} + 3^{2}) + . . .

= \sum_{i = 1}^{n} \sum_{j = 1}^{i} j^{2}

整个区域的次数是：

(1 * n + 2 * (n - 1) + . . . + n * 1)^{2}

= (1 + (1 + 2) + (1 + 2 + 3) + . . .)^{2}

= (\sum_{i = 1}^{n} \sum_{j = 1}^{i} j)^{2}

得黄色区域出现的概率是：

\frac{\sum_{i = 1}^{n} \sum_{j = 1}^{i} j^{2}}{(\sum_{i = 1}^{n} \sum_{j = 1}^{i} j)^{2}}

然后发现自己根本不会算！

于是我无耻地打开了mma：

于是 $O (1)$ 解就这样~~推出来了~~。

另外，当n趋近于正无穷时，平局的概率是0，所以获胜的概率为1/2.

/*
 * @Author: junyu33 
 * @Date: 2020-06-09 16:05:43 
 * @Last Modified by:   junyu33 
 * @Last Modified time: 2020-06-09 16:05:43 
 */
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int mod=998244353;
int n,ans;
int qpow(int m,int n){int ans=1;for(;n;n>>=1){if(n&1)ans=ans*m%mod;m=m*m%mod;}return ans;}
int inv(int x){return qpow(x,mod-2);}
signed main(){
   cin>>n;n%=mod;
   if(n==0){cout<<inv(2);return 0;}
   int a=(n*n%mod+2*n-3)%mod,b=2*n%mod*(n+2)%mod;
   cout<<a*inv(b)%mod;
}