Rathee's trilogy — CrypTFlow2, SIRNN, and SecFloat

Background

Notation: Let $\lambda$ be the security parameter, and the length of the secret-shared integer be $l$-bits.

Assume having the following basic knowledge in Multi-Party Computation:

• 1-out-of-$k$ ${\text{OT}}_l$ can be implemented using public-key cryptography or similar methods, with a communication cost of $2\lambda +kl$ per instance; using IKNP, this can be reduced to $\lambda +kl$.
• Addition and scalar multiplication based on 2-party additive secret sharing are almost free (no communication overhead).
• Secure multiplication operations for 2-party computation can be implemented using Beaver triples. One secure multiplication operation requires a total communication cost of $2l$.

For floating-point storage, we use IEEE 754 Float32 (single-precision standard):

• $(-1{)}^S\times (1.M)\times 2^{E-bias}$

• Sign bit $S$ 1 bit, exponent $E$ 7 bits, mantissa $M$ 23 bits, $bias=127$

• Round-to-nearest-ties-to-even

IEEE 754 Addition

Without loss of generality, assume $x\ge y$. To compute $z=x+y$, where:

$$x=(-1{)}^{S_x}\cdot (1.M_x)\cdot 2^{E_x},y=(-1{)}^{S_y}\cdot (1.M_y)\cdot 2^{E_y}$$

The steps are as follows:

1. Exponent alignment. If $E_x>E_y$, right-shift the mantissa of $y$: $M_y\leftarrow \frac{1.M_y}{2^{E_x-E_y}},E\leftarrow E_x,M_x\leftarrow (1.M_x)$.
2. Mantissa addition. Consider the signs of $S_x$ and $S_y$. If they have the same sign, calculate $M=M_x+M_y$. If they have different signs, subtract the smaller from the larger to get the absolute value of the difference $M=|M_x-M_y|$, and attach the correct sign $S$.
3. Normalization. Clearly, $max\{M_x+M_y,|M_x-M_y|\}<4$, so $M$ only needs to be right-shifted at most once (corresponding to adding 1 to the exponent $E$). If $M=0$, skip directly to step 4. Otherwise, repeatedly left-shift and decrement $E$ until $M\in [1,2)$.
4. Write the result. Finally, remove the leading 1 of $M$, and use the final $S,E,M$ as the new 32-bit floating-point result.
5. Rounding issues may arise in the following four steps: $M_y\leftarrow \frac{1.M_y}{2^{E_x-E_y}}$, $M=M_x+M_y$, $M=|M_x-M_y|$, and right-shifting $M$ by one bit.

IEEE 754 Multiplication

Multiplication is relatively simple because it doesn't involve comparing the magnitudes of numbers.

1. XOR the sign bits. $S=S_x\oplus S_y$.
2. Add the exponents. $E=E_x+E_y-bias$.
3. Multiply the mantissas. $M=(1.M_x)\cdot (1.M_y)$, the result is in the range $[1,4)$.
4. Normalize. If the result $\ge 2$, increment $E$ and right-shift $M$ by one bit, then remove the most significant bit of $M$.
5. Rounding operations are involved in the steps of $M=(1.M_x)\cdot (1.M_y)$ and right-shifting $M$ by one bit.

Rounding Method

Let $d,g,f$ represent the least significant bit (decision bit), the most significant discarded bit (guard bit), and the remaining discarded bits (sticky bit) of $M$, respectively. The "round half to even" rule can be formally expressed as the following formula:

$$c=g\wedge (d\vee f)$$

Simply put, a carry ($c=1$) is only possible when $g=1$. In this case, if $f=1$ (definitely greater than 0.5) or $d=1$ (exactly 0.5, but the result must be even), then a carry occurs ($c=1$).

Note that normalization may be required after rounding.

Building Blocks

Below, we will explain how the entire protocol is constructed using a bottom-up approach.

${\mathcal{F}}_{MUX}$

The ideal function we need to implement is MUX(b,x)=(b==1?x:0). That is, for a Boolean secret share $[c]=(c_0,c_1),c_i\in \{0,1\}$ and an arithmetic secret share $[a]=(a_0,a_1),a\in Z_n$, the output should be $[a\cdot c]$. The steps are as follows:

SETUP: $P_0$ holds $a_0,c_0$, and $P_1$ holds $a_1,c_1$.

• $P_0$ and $P_1$ each generate random numbers $r_0,r_1\in Z_n$.
• $P_0$ sets $(s_0,s_1)$ based on the value of $c_0$. If $c_0=0$, let $(s_0,s_1)=(-r_0,-r_0+a_0)$, otherwise it is $(-r_0+a_0,-r_0)$.
• $P_0$ acts as the sender and performs one round of 1-out-of-2 OT with $P_1$. $P_0$ provides two messages $(s_0,s_1)$, and $P_1$ provides $c_1$ and ultimately obtains $x_1=s_{c_1}$.
• $P_1$ sets $(t_0,t_1)$ based on the value of $c_1$. If $c_1=0$, let $(t_0,t_1)=(-r_1,-r_1+a_1)$, otherwise it is $(-r_1+a_1,-r_1)$.
• Another round of OT is performed, and $P_0$ obtains $x_0=t_{c_0}$.
• $P_0$ contributes $r_0+x_0$, and $P_1$ contributes $r_1+x_1$. The sum is $(r_0+r_1)+(x_0+x_1)$.

We list four possible cases for $(c_0,c_1)$:

$(s_0,s_1)=(-r_0+c_0{a}_0,-r_0+a_0(1-c_0))$，$(t_0,t_1)=(-r_1+c_1{a}_1,-r_1+a_1(1-c_1))$

$x_0=t_{c_0},x_1=s_{c_1}$

$c_0$	$c_1$	$x_0$	$x_1$	$(r_0+r_1)+(x_0+x_1)$
0	0	$-r_1+c_1{a}_1$	$-r_0+c_0{a}_0$	0
0	1	$-r_1+c_1{a}_1$	$-r_0+a_0(1-c_0)$	$a$
1	0	$-r_1+a_1(1-c_1)$	$-r_0+c_0{a}_0$	$a$
1	1	$-r_1+a_1(1-c_1)$	$-r_0+a_0(1-c_0)$	0

The result is exactly equal to $[a\cdot c]$, therefore the protocol is correct.

The communication cost is the overhead of two rounds of IKNP-OT, which is $2(\lambda +2l)=2\lambda +4l$. However, Section 3.1.1 of CryptoFlow2 can optimize the communication overhead to $2\lambda +2l$.

${\mathcal{F}}_{AND}$

This is a direct implementation with Beaver triples, the communication overhead is $(\lambda +16)+4$. (See Appendix A1 of CryptoFlow2)

${\mathcal{F}}_{OR}$

We have $[x\vee y]=[x\oplus y]\oplus [x\wedge y]$. Therefore, let $[x\wedge y]=(z_0,z_1)$, so each party can directly compute $x_i\oplus y_i\oplus z_i$. The communication cost is the same as for ${\mathcal{F}}_{AND}$, which is $\lambda +20$.

${\mathcal{F}}_{EQ}$

We divide $x$ and $y$ into $m$-bit blocks. Consider comparing a pair of blocks $x_j,y_j$. We use 1-out-of-$2^m$ Oblivious Transfer (OT):

• $P_0$ randomly selects $(e{q}_{0,j}{)}_0$ and prepares messages $t_{j,k}=(e{q}_{0,j}{)}_0\oplus (x_j==k)$ for $k\in [0,2^m-1]$.
• $P_0$ uses these $2^m$ messages as input to the OT, $P_1$ inputs $y_j$, and obtains $(e{q}_{0,j}{)}_1$.
• If and only if $x_j=y_j$, we have $(e{q}_{0,j}{)}_0\oplus (e{q}_{0,j}{)}_1=1$, which completes the secure equality comparison of $x_j$ and $y_j$.

We can extend the $m$-bit comparison to $2m$-bit using a tree structure and ${\mathcal{F}}_{AND}$ gates, calculating $(e{q}_{1,j}{)}_i=(e{q}_{0,j}{)}_i\wedge (e{q}_{0,j+m}{)}_i$, finally completing the comparison for the entire length. The communication complexity is $\lceil \frac{l}{m}\rceil (2\lambda +2^m)+\lceil \frac{l}{m}\rceil (\lambda +20)$, and the number of rounds is $\log l$.

${\mathcal{F}}_{GT/LT}$

The approach still involves block processing. First, we compute the result $1\{x_j<y_j\}$ for blocks of length $m$, which can be done using 1-out-of-$2^m$ OT. $P_0$ only needs to randomly generate $(l{t}_{0,j}{)}_0$ and prepare $2^m$ messages $t_{j,k}=(l{t}_{0,j}{)}_0\oplus 1\{x_j<k\}$.

Then, during the merging process, we prioritize the higher-order bits: $1\{x<y\}=1\{x_H<y_H\}\oplus (1\{x_H=y_H\}\wedge 1\{x_L<y_L\})$.

The communication cost is less than $\lambda (4q)+2^m(2q)+22q$. With $m=4$ and $q=l/4$, this becomes $\lambda l+13.5l$, and the number of rounds is $\log l$.

${\mathcal{F}}_{LUT}$

Assume the LUT has $2^m$ entries, each with $n$ bits.

SETUP: $P_0$ randomly selects an index $r\in \{0,1{\}}^m$, and a share $T^0[i]\in Z_{2^n}$ for each entry $i\in \{0,1{\}}^m$, which is a masked version of the LUT $L$.

• For each $s\in \{0,1{\}}^m$, $P_0$ constructs $M_s[i]=L[i\oplus r\oplus s]\oplus T^0[i],\mathrm{\forall }i\in \{0,1{\}}^m$.
• $P_0$ performs a 1-out-of-$2^m$ ${\text{OT}}_n$ with $P_1$ (who selects $s$) using these $2^m$ messages of length $n$-bits each. The cost is $2\lambda +2^{m}n$.
• $P_1$ sets $T^1\leftarrow M_s$. Now $P_0$ holds $(T^0,r)$, and $P_1$ holds $(T^1,s)$.
• In the online phase, $P_0$ sends $u=x_0\oplus r$, and $P_1$ sends $v=x_1\oplus s$. Both parties simultaneously compute $i^{\ast }=u\oplus v=x\oplus r\oplus s$. Finally, $P_0$ and $P_1$ store $T^0[i^{\ast }]$ and $T^1[i^{\ast }]$ respectively, which together reconstruct $L[x]$. The communication cost of $2m$ is negligible.

${\mathcal{F}}_{Wrap}$

If we want to compute $1\{a+b>2^n-1\}$, this is equivalent to computing $1\{2^n-1-a<b\}$. Therefore, we can directly use ${\mathcal{F}}_{GT/LT}$.

${\mathcal{F}}_{B2A}$

$P_0$ and $P_1$ each hold a Boolean share of a single bit $c=c_0\oplus c_1$, where $c\in \{0,1\}$, and ultimately obtain $d=d_0+d_1(\mathrm{mod}{2}^n)$ such that $d=c$.

• $P_0$ randomly selects $x\in Z_{2^n}$, generates the pair $(x,c_0+x)$, and performs a 1-out-of-2 ${\text{COT}}_n$ with $P_1$ (who holds input $c_1$). $P_1$ receives the result $y_1$. $P_0$ sets $y_0=2^n-x$.
• Both parties perform local linear correction: $P_0$ computes $d_0=c_0-2y_0$, and $P_1$ computes $d_1=c_1-2y_1$.

Let's verify the result: $d_0+d_1=c_0+c_1-2(y_0+y_1)$.

• When $c_1=0$, $y_0+y_1=(2^n-x)+x=2^n$, so $d_0+d_1=c_0+c_1(\mathrm{mod}{2}^n)$.
• When $c_1=1$, $y_0+y_1=(2^n-x)+(c_0+x)=2^n+c_0$, so $d_0+d_1=c_0+c_1-2c_0=1-c_0$. But in this case, $c=c_0\oplus 1=1-c_0$, so $d=c$ still holds.

The communication cost is one 1-out-of-2 ${\text{COT}}_n$, with a cost of $\lambda +n$.

${\mathcal{F}}_{ZExt}$

Having already defined ${\mathcal{F}}_{Wrap}$ and ${\mathcal{F}}_{B2A}$, constructing ${\mathcal{F}}_{ZExt}$ is a natural step. For $m$-bit additive sharing, we attempt to zero-extend it to $n$-bit $(n>m)$. First, we check if there is a carry between the two shares (using ${\mathcal{F}}_{Wrap}$), and then convert the resulting Boolean carry $w$ into an arithmetic value in $Z_{2^{n-m}}$ using ${\mathcal{F}}_{B2A}$.

However, since we are only performing a zero-extension operation, the sum of the two shares cannot produce a carry at the $m$-th bit. Therefore, both parties must subtract a share of $2^m$ in $Z_{2^n}$. Since $m$ is public, this can be done locally.

The cost is $\text{Comm}({\mathcal{F}}_{Wrap}+{\mathcal{F}}_{B2A})=\lambda m+14m+\lambda +(n-m)=\lambda (m+1)+13m+n$.

${\mathcal{F}}_{TR}$

Since we have ${\mathcal{F}}_{ZExt}$ for extending from smaller to larger bit lengths, we naturally also have the reverse operation, ${\mathcal{F}}_{TR}$. We assume that we truncate the lower $s$ bits from an $l$-bit number and output the remaining higher $l-s$ bits (this is essentially equivalent to x >> s):

SETUP: $P_b$ splits the original share $x_b$ into $u_b||v_b$, where the former is $l-s$ bits and the latter is $s$ bits. It can be proven that:

$$TR(x,s)=u_0+u_1+Wrap(v_0,v_1,s)$$

The cost is $\text{Comm}({\mathcal{F}}_{Wrap}+{\mathcal{F}}_{B2A})=(\lambda s+14s)+(\lambda +(l-s))=\lambda (s+1)+13s+l$.

${\mathcal{F}}_{CrossTerm}$

${\mathcal{F}}_{CrossTerm}$ is similar to secure multiplication using Beaver triples, but the difference is that in the latter, both $P_0$ and $P_1$ know a part of the shares of $x$ and $y$. The applicable condition for ${\mathcal{F}}_{CrossTerm}$ is that $P_0$ exclusively holds $x$, and $P_1$ exclusively holds $y$, and finally each obtains a share of $x\ast y$ of length $l=m+n$.

• $P_0$ writes its $x$ in binary as $x=\sum _{i=0}^{m-1}{x}_i{2}^i,x_i\in \{0,1\}$.
• For $i\in [0,m-1]$, a 1-out-of-2 ${\text{COT}}_{l-i}$ is called: $P_0$ holds $x_i$, $P_1$ holds $y$, generating $⟨t_i{⟩}^{l-i}$ such that $t_i=x_i\cdot y$.
• Both parties locally compute $⟨z{⟩}^l=\sum _{i=0}^{m-1}⟨t_i{⟩}^{l-i}$. Clearly, the sum of the two shares is the product $x\cdot y$.

The total communication cost is $\sum _{i=0}^{m-1}(\lambda +(l-i))=m\lambda +ml-\frac{m(m-1)}{2}=O(m\lambda +mn)$.

${\mathcal{F}}_{UMult}$

The semantics are that both parties hold $x=x_0+x_1(\mathrm{mod}{2}^m)$ and $y=y_0+y_1(\mathrm{mod}{2}^n)$, and the goal is to compute $z=x\cdot y\in Z_{2^{m+n}}$.

Here, we cannot directly use Beaver triples because they are ring-agnostic, which might lead to unknown wrap-around issues. One approach is to extend both $x$ and $y$ to a sufficiently large ring, perform secure multiplication, and then truncate the result. However, this approach has two problems: first, ${\mathcal{F}}_{TR}$ performs high-order truncation rather than low-order truncation, requiring modifications to the protocol; second, this method is computationally expensive, making it less efficient than the dedicated ${\mathcal{F}}_{UMult}$ protocol described below.

We now need to compute $(x_0+x_1)(y_0+y_1)=x_0{y}_0+x_1{y}_1+x_0{y}_1+x_1{y}_0$. The first two terms can be computed offline by $P_0$ and $P_1$ respectively. The latter two terms involve the ${\mathcal{F}}_{CrossTerm}$ mentioned earlier. In short, we have the complete $x_0{y}_0$ stored at $P_0$, $x_1{y}_1$ stored at $P_1$, and a portion of $⟨x_0{y}_1⟩$ and $⟨x_1{y}_0⟩$ held by both parties. The function of ${\mathcal{F}}_{UMult}$ is to securely combine these four terms and handle the wrap-around issue.

• First, we need to consider whether $x_0+x_1$ and $y_0+y_1$ overflow, so we need ${\mathcal{F}}_{Wrap}$ to detect and obtain two overflow bits $w_x,w_y$.
• Then we can use ${\mathcal{F}}_{MUX}$ to compute the shares $⟨g⟩,⟨h⟩$ of g=w_y?x:0 and h=w_x:y:0, handling the possible overflow difference.
• Finally, $P_b$ outputs $x_b{y}_b+⟨x_0{y}_1{⟩}_b+⟨x_1{y}_0{⟩}_b-2^n⟨g{⟩}_b-2^m⟨h{⟩}_b$.

Let's try adding the two shares together: $\sum _b(x_b{y}_b+⟨x_0{y}_1{⟩}_b+⟨x_1{y}_0⟩)=(x_0+x_1)(y_0+y_1)$

And $\sum _b(-2^n⟨g{⟩}_b-2^m⟨h{⟩}_b)=-2^{n}g-2^{m}h=-2^n(w_y\cdot x)-2^m(w_x\cdot y)$

Combining them, $z=(x_0+x_1)(y_0+y_1)-w_y\cdot (x\cdot 2^n)-w_x\cdot (y\cdot 2^m)$

$=(x+w_x{2}^m)(y+w_y{2}^n)-w_y\cdot (x\cdot 2^n)-w_x\cdot (y\cdot 2^m)=xy$, which cancels out perfectly.

Let $\nu =max(m,n),l=m+n$. The paper provides the specific cost, which is of the order $O(\lambda \nu +{\nu }^2)$. Compared to the Beaver triple method (including the generation of multiplication triples), which has a complexity of $O(\lambda l+l^2)$, the order is the same, but the paper claims that ${\mathcal{F}}_{UMult}$ requires 1.5 times less communication.

The principle of ${\mathcal{F}}_{SMult}$ is similar to ${\mathcal{F}}_{UMult}$, and the communication volume is exactly the same, so we omit the details here.

${\mathcal{F}}_{DigDec}$

The function is to split an $l$-bit share $⟨x⟩$ into $c=\lceil \frac{l}{d}\rceil$ blocks of $d$ bits each, resulting in $\{⟨z_i⟩{\}}_{i=0}^{c-1}$, where $x=z_{c-1}||z_{c-2}||\cdots ||z_0$. Clearly, performing this operation locally would lead to a wrap-around problem.

Of course, the solution to this problem is also straightforward. First, use ${\mathcal{F}}_{wrap}$ to determine if the two shares of $⟨x_{[0,d-1]}⟩$ overflow, and obtain the share of the overflow result $⟨c_0⟩$. Let $⟨z_0⟩=⟨x_{[0,d-1]}⟩-2^d⟨c_0⟩$, and add $⟨c_0⟩$ to the higher-order bits $⟨x_{[d,l-1]}⟩$ of both parties. Finally, recursively perform this process.

The complexity is equivalent to the cost of $(c-1)$ calls to ${\mathcal{F}}_{wrap}$, which is $(c-1)(\lambda d+14d)$.

${\mathcal{F}}_{MSNZB-P}$

The detection of the global index corresponding to the highest non-zero bit in the $i$-th $d$-bit block can also be understood as $\lfloor {\log }_2(z_i)\rfloor +i\cdot d$. The specific implementation method here is to solve it directly using ${\mathcal{F}}_{LUT}$. However, there is a problem: when $z_i=0$, the expression on the right does not have the same semantics as the implementation on the left. The authors choose to leave the result undefined when $z_i=0$, leaving it to the higher-level protocol to handle.

I don't quite understand this point. The case where $z_i=0$ can also be solved directly using ${\mathcal{F}}_{LUT}$ without increasing communication costs.

In short, the communication volume is equivalent to a 1-out-of-$2^d$ ${\text{OT}}_{\lceil {\log }_{2}l\rceil }$ implementation, so the communication volume is $2\lambda +2^d\lceil {\log }_{2}l\rceil$.

${\mathcal{F}}_{Zeros},{\mathcal{F}}_{OneHot}$

The former means determining whether a vector of length $d$ (or a $d$-bit number) is zero. The latter transforms a share $⟨k⟩\in [0,l-1]$ into a vector share of length $l$, such that the sum is $(0,0,\dots ,1,\dots ,0)$, where only the $k$-th element is 1.

These two can be implemented using 1-out-of-$2^d$ OT and 1-out-of-$l$ OT${}_l$ respectively, with costs of $2\lambda +2^d$ and $2\lambda +l^2$. Although the latter has a higher cost, it is only called once at the end of the parent protocol ${\mathcal{F}}_{MSNZB}$, so the total cost is still acceptable.

${\mathcal{F}}_{MSNZB}$

The meaning is that given an input $⟨x{⟩}^l$, we compute the value $k$ of the highest zero bit of $l$, and output a vector share such that the sum is $(0,0,\cdots ,1,\cdots ,0)$, where only the $k$-th vector is 1. For simplicity, here I assume that ${\mathcal{F}}_{MSNZB-P}$ is well-defined (i.e., it handles the case where $z_i=0$). Let $\iota =\lceil {\log }_{2}l\rceil$:

• First, compute the input $⟨x{⟩}^l$ using ${\mathcal{F}}_{DigDec}$ to obtain $⟨y_i{⟩}^d$, then for each $i$, call ${\mathcal{F}}_{MSNZB-P}$ to obtain $⟨u_i{⟩}^{\iota }$.
• Call ${\mathcal{F}}_{Zeros}$ to obtain Boolean shares $⟨v_i⟩$, and use ${\mathcal{F}}_{AND}$ (i.e., Beaver triple) for any $i=c-2,\cdots ,0$ to compute $w_i=w_{i+1}\wedge v_{i+1}$. Thus, $w_i=\prod _{j>i}{v}_j$. The value of the most significant non-zero bit is the last one from largest to smallest that satisfies $w_i=1$.
• For the most significant digit, let $⟨z_{c-1}^{\prime }{⟩}^{\iota }=⟨u_{c-1}{⟩}^{\iota }$, and for the remaining $i=c-2,\cdots ,0$, $z_i^{\prime }=\text{MUX}(w_i,u_i)$.
• Finally, locally compute $\tilde{z}=\sum _{i=0}^{c-1}{z}_i^{\prime }$, and call ${\mathcal{F}}_{OneHot}$ to obtain the final Boolean vector $\{⟨z_k⟩{\}}_{k\in [0,l-1]}$.

Summary

Primitive	Dependent Primitives	Function	Communication Overhead
${\mathcal{F}}_{MUX}$	$(\genfrac{}{}{0ex}{}{2}{1})-{\text{OT}}_l$	Ternary operator of length $l$ bits	$2\lambda +2l$
${\mathcal{F}}_{OR}$	${\mathcal{F}}_{AND}$, i.e., Beaver triple	Logical OR	$\lambda +20$
${\mathcal{F}}_{EQ}$	$(\genfrac{}{}{0ex}{}{2^m}{1})-\text{OT},{\mathcal{F}}_{AND}$	Arithmetic equality of length $l$ bits	$<\frac{3}{4}\lambda l+9l$
${\mathcal{F}}_{LT/GT}$	$(\genfrac{}{}{0ex}{}{2^m}{1})-\text{OT},{\mathcal{F}}_{AND}$	Arithmetic comparison of length $l$ bits	$<\lambda l+14l$
${\mathcal{F}}_{LUT}$	$(\genfrac{}{}{0ex}{}{2^m}{1})-{\text{OT}}_n$	Lookup table with $m$-bit input and $n$-bit output	$2\lambda +2^{m}n$
${\mathcal{F}}_{ZExt}$	${\mathcal{F}}_{Wrap},{\mathcal{F}}_{B2A}$	Zero extension from $m$ bits to $n$ bits	$\lambda (m+1)+13m+n$
${\mathcal{F}}_{TR}$	${\mathcal{F}}_{Wrap},{\mathcal{F}}_{B2A}$	Truncation of $l$ bits to the high $l-s$ bits	$\lambda (s+1)+l+13s$
${\mathcal{F}}_{UMult},{\mathcal{F}}_{SMult}$	${\mathcal{F}}_{CrossTerm},{\mathcal{F}}_{Wrap},{\mathcal{F}}_{MUX}$	Unsigned/signed multiplication of length $m,n$ bits	$O(\lambda l+l^2)$
${\mathcal{F}}_{MSNZB}$	${\mathcal{F}}_{DigDec},{\mathcal{F}}_{MSNZB-P},{\mathcal{F}}_{OneHot}$, etc.	Index of the highest non-zero bit in a number of length $l$ bits	$\le \lambda (5l-4)+l^2$

Primitives

We have finally built all the basic protocols corresponding to the secfloat paper, and now we move on to the important primitives constructed in this paper.

${\mathcal{F}}_{FPcheck}^{p,q}$

This is used to check whether floating-point numbers overflow or underflow given floating-point parameters $p$ and $q$ (the IEEE 754 standard uses $p=8,q=23$). This is an innovative aspect of this paper: the ability to choose the floating-point parameters independently, without necessarily adhering to the IEEE 754 format.

α = (z, s, e, m)
if 1{e > 2^{p-1} - 1} then
   m = 2^q; e = 2^{p-1}
if 1{z = 1} ∨ 1{e < 2 - 2^{p-1}} then
   m = 0; e = 1 - 2^{p-1}; z = 1
Return (z, s, e, m)

This logic aligns with the paper's approach to handling overflows. Here's a brief description of how the protocol works:

• The second line involves a ${\mathcal{F}}_{GT/LT}$ operation because $p$ is public; the fourth line involves an ${\mathcal{F}}_{EQ}$ operation.
• The assignment operations in the third and fifth lines do not raise privacy concerns because the assignment constant $c$ is public; therefore, $P_0=0$ and $P_1=c$ can be used directly.
• The if-branch essentially represents the specific semantics of the ${\mathcal{F}}_{MUX}$ operation.

${\mathcal{F}}_{TRS}^{l,s}$

${\mathcal{F}}_{TRS}$ builds upon ${\mathcal{F}}_{TR}$ by adding a carry determination for the floating-point sticky bit $S$. A carry operation is performed if any of the discarded lower $s$ bits is 1, and $LSB(x)=0$. This is equivalent to (x >> s) | (x & (2**s - 1) != 0). The right shift is handled by ${\mathcal{F}}_{TR}$ (or a combination of ${\mathcal{F}}_{Wrap}$ and ${\mathcal{F}}_{B2A}$), but an additional ${\mathcal{F}}_{Zeros}$ operation is required afterward, which is costly.

Since ${\mathcal{F}}_{Zeros}$ is also equivalent to checking whether the sum of two shares is $2^s$, or whether both are 0, its essence is also a comparison operation (or an ${\mathcal{F}}_{Wrap}$ operation). Therefore, the authors chose to combine ${\mathcal{F}}_{Wrap}$ and ${\mathcal{F}}_{Zeros}$ into ${\mathcal{F}}_{Wrap\mathrm{\&}All0s}$, with a cost equivalent to only one comparison operation and one ${\mathcal{F}}_{AND}$ operation (there is a typo in the paper; it's not the cost of two ${\mathcal{F}}_{AND}$ operations).

${\mathcal{F}}_{RNTE}^l$

${\mathcal{F}}_{RNTE}$ is equivalent to a right shift with rounding, $x{\gg }_{R}r$. As discussed previously, the IEEE rounding logic is as follows:

$$c=g\wedge (d\vee f)$$

We first use TRS(x, r-2) to check if the bits after $f$ are 1. If they are, we add them back to ensure the sticky bit logic is correct. At this point, the last three bits of $x$ are $d,g,f$. Then, we use ${\mathcal{F}}_{LUT}$ to hardcode this 8-bit rounding logic into the result $c$. Finally, we call TR(x, 2) and add the rounding result $c$.

${\mathcal{F}}_{Roun{d}^{\ast }}^{p,q,Q}$

Given the floating-point number $\alpha =(z,s,e,m)$, round the normalized mantissa $m$ from $Q$-bit precision to $q$-bit precision, and handle any carry overflow resulting from the rounding. Note that $m$ is represented in fixed-point form, meaning the mantissa $1.M$ corresponds to the fixed-point number $m=(1.M)\times 2^Q$. Therefore, the range of $m$ is $[2^Q,2^{Q+1})$. The protocol logic is as follows:

if 1{m >= 2^{Q+1} − 2^{Q−q−1}} then
   Return (e+1, 2^q)
else
   Return (e, m >>R (Q−q))

The following explains the correctness of the code's logic. The mantissa is considered in two cases:

• First, when the first $q$ bits of the mantissa are all 1s, and the $(q+2)$-th bit (corresponding to $2^{Q-q-1}$) is also 1. This exactly satisfies the minimum rounding condition of RNTE, so the entire $Q$ bits will be rounded to 2.0. After normalization, $e=e+1$, and the mantissa $m$ returns to its original $q$-bit precision normalized form $2^q$.
• Second, in most cases where rounding does not require further normalization, simply perform a right shift of $Q-q$ bits with rounding according to the previous ${\mathcal{F}}_{RNTE}$ protocol.

${\mathcal{F}}_{FPAdd}^{p,q}$

In the Background Chapter, we summarized the method for ordinary floating-point addition. Below, we will show how this method corresponds to pseudocode:

1. Exponent alignment. If $E_x$ > $E_y$, left-shift the mantissa of $x$: $M_x\leftarrow (1.M_x)2^{E_x-E_y},E\leftarrow E_y$.

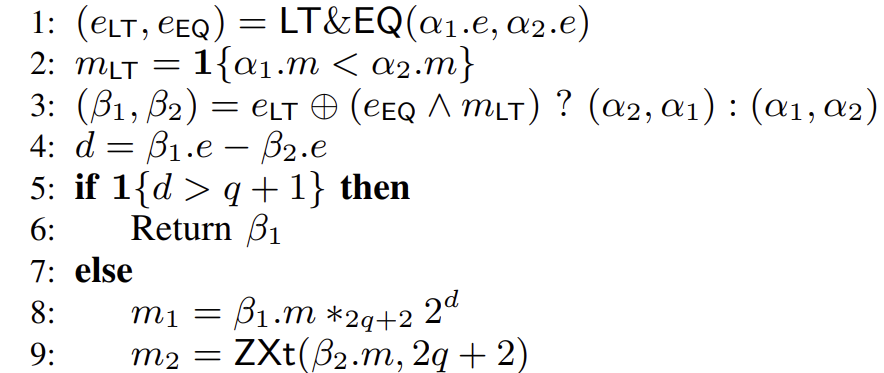
2. Add the mantissas. Consider the signs of $S_x$ and $S_y$. If they have the same sign, calculate $M=M_x+M_y$. If they have different signs, subtract the smaller one from the larger one to get the absolute value of the difference, $M=|M_x-M_y|$, and attach the correct sign $S$.

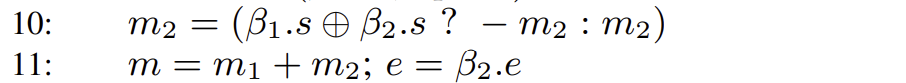
Here we consider the cases of same and different signs. When the signs are the same, the XOR of the sign bits of ${\beta }_1$ and ${\beta }_2$ is 0; otherwise, it is 1. Therefore, when ${\beta }_1.s\oplus {\beta }_2.s=1$, we change the sign of $m_2$ to perform the subtraction operation.

3. Normalization. Here we find the most significant bit in the sum $m$. To ensure sufficient space for rounding, the protocol zero-extends $m_1$ and $m_2$, which have precision $q$, to $2q+2$ bits in the first step (but note that the precision is $2q+1$). Assuming the result of MSNZB is $k$, normalizing the most significant bit (i.e., aligning it with the $2q+1$ bits used in the subsequent Round* protocol) requires a left shift of $2q+1-k$ bits, corresponding to multiplication by $K=2^{2q+1-k}$.

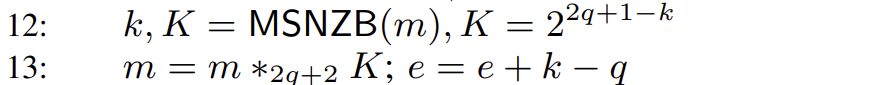
Regarding the calculation of the exponent, since it was shifted left by $2q+1-k$ bits, and also because the precision change added $q+1$, the new exponent becomes $e=e-(2q+1-k)+(q+1)=e+k-q$.

4. Writing the result. Finally, a round of rounding is performed using ${\mathcal{F}}_{Roun{d}^{\ast }}^{p,q,2q+1}$. Since $|m_1|>|m_2|$, the sign bit is determined by ${\beta }_1.s$. Finally, check if the normalized result is within the valid range of floating-point numbers.

${\mathcal{F}}_{FPMul}^{p,q}$

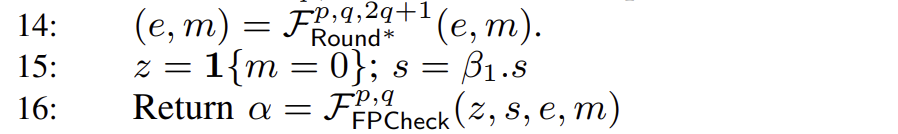
1. XOR the sign bits. $S=S_x\oplus S_y$. (Line 7)
2. Add the exponents. $E=E_x+E_y-bias$. (Line 1, the paper sets $bias=0$ here)
3. Multiply the mantissas. $M=M_x\cdot M_y$, the result is in the range $[2^{2q},2^{2q+2})$. (Line 2)
4. Normalization. If the result $\ge 2^{2q+1}$, increment $E$ and right-shift $M$ by one bit, finally removing the most significant bit of $M$.

If the result $\ge 2^{2q+1}$, follow the else branch on line 6, otherwise follow the if branch on line 4.

5. Rounding operations are involved in the steps of $M=M_x\cdot M_y$ and right-shifting $M$ by one bit. (i.e., ${\mathcal{F}}_{RNTE}^l$ on lines 4 and 6)

Math Functions

In the book これでなっとく！数学入門――無限・関数・微分・積分・行列を理解するコツ written by 瀬山士郎, a following excerpt explained how to calculate trigonometric functions on computers/calculators (I don't have the English version of this book, so I summarized it using ChatGPT):

The pages explain how trigonometric functions, especially the sine function, are calculated. Through a short classroom dialogue, the text raises the question of how a calculator can produce a value such as $\sin (0.7)$. It then explains that trigonometric functions cannot be represented by finite polynomials, but they can be expressed as infinite power series, known as Taylor (or Maclaurin) expansions. Using $\sin x$ as an example, the book shows its series expansion and explains that by taking only the first few terms, one can obtain an approximate value of $\sin (0.7)$. The more terms used, the more accurate the result becomes. Although the series is infinite and never truly ends, calculators compute enough terms to achieve practical accuracy, which is sufficient for most real-world applications.

${\mathcal{F}}_{FP\sin \pi }^{8,23}$

Based on this idea, we can actually elaborate on how a computer calculates $\sin x$.

1. First, use trigonometric identities to reduce the range of $x$ to $[0,\pi /2]$. (Range reduction)

This is the approach used in the paper, but in practice, rounding to $[-\pi /4,\pi /4]$ and then using the double-angle formula reduces the error by an order of magnitude.

2. Use Taylor series expansion for approximation, for example, $\sin x\approx x-\frac{1}{6}{x}^3+\frac{1}{120}{x}^5$. (Polynomial Evaluation)
3. Use Horner's method: $x-\frac{1}{6}{x}^3+\frac{1}{120}{x}^5=((\frac{1}{120}{x}^2-\frac{1}{6})x^2+1)x$, to reduce the number of multiplications and lower the error.

These operations only require floating-point addition and multiplication. The coefficients of the polynomial are relatively fixed and can be obtained through a lookup table.

We now correspond this to the specific primitive function ${\mathcal{F}}_{FP\sin \pi }^{8,23}$, which is the calculation of $\sin \pi x$. The steps are as follows:

1. First, handle special cases: When $|x|>2^{23}$, since $q=23$, it exceeds the precision of the mantissa, so $x$ must be an integer. Therefore, $\sin \pi x=0$. Another special case is when $|x|<2^{-14}$, in which case $\sin \pi x\approx \pi x$, and the error is within the error of the floating-point representation of $x$ itself.

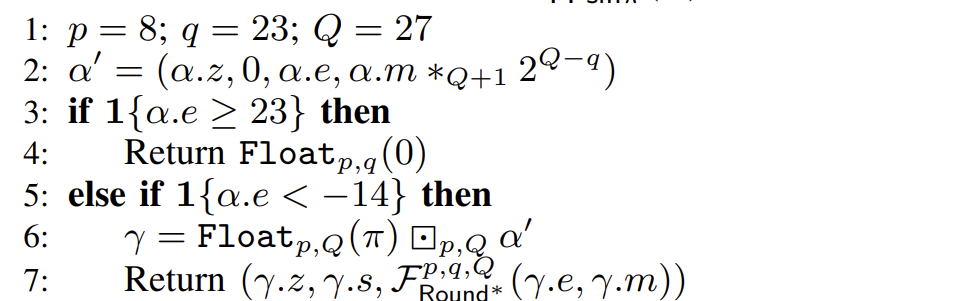
2. Range Reduction Step: The goal is to calculate the parity bit $a\in \{0,1\}$ and the interval $\delta$ from the input $\alpha$. Let $|\alpha |=2K+a+n$. If $n<0.5$, then $\delta =n$; otherwise, $\delta =1-n$. Therefore, $\sin \pi \alpha =(-1{)}^{a\oplus 1\{\alpha <0\}}\sin \pi \delta$.

m = α.m * 2^{α.e + 14}
a = TR(m, q+14); n = m mod 2^{q+14}

Transform $\alpha$ into an integer. Since $|\alpha |=2^{\alpha .e}\cdot \frac{\alpha .m}{2^q}$, we have $m=\alpha .m\cdot 2^{\alpha .e+14}\approx |\alpha |\cdot 2^{q+14}$. Then $a$ is the integer part of $|\alpha |$, and $n$ is the fractional part of $|\alpha |$.

f = (n > 2^{q+13} ? 2^{q+14} - n : n)
k,K = MSNZB(f); f = f * K
z = 1{f=0}; e = (z ? -2^{p-1}+1 : k - q - 14)

The first line ensures that $f=\delta \cdot 2^{q+14}$. The second line finds the most significant bit of $f$, thus normalizing $f$, and the third line sets the correct exponent bits $e$.

When $f=0$, $\sin \pi \alpha =0$. The zero bit $z$ is set to $1$, and the exponent bits $e$ are set to $-2^{p-1}+1$ according to the convention in the paper.

δ = (z, 0, e, TR(f, q+14−Q))

Finally, the fixed-point number $f$ is stored again with $Q$ bits of precision and combined with other parameters to form the floating-point number $\delta$.

3. Polynomial Evaluation Step: Note that the paper uses the Remez method and other more accurate approximation methods, rather than Taylor expansion:

if 1{δ.e < −14} then
   µ = Float_{p,Q}(π) ⊗_{p,Q} δ

Previously, in the special case where $|\delta |\le 2^{-14}$, we had $\sin \pi x\approx \pi x$.

if 1{δ.e < −5} then
   idx1 = δ.e + 14 mod 2^4
   (θ1, θ3, θ5) = GetC_{4,9,5,p,Q}(idx1, Θ1_sin, K1_sin)

Consider the case where $2^{-14}<|\delta |<2^{-5}$. Here, the GetC function performs a table lookup operation. By selecting the constant class K1_sin, it retrieves the corresponding parameters (θ1, θ3, θ5) from the table Θ1_sin using the index idx1 (which is the lower 4 bits of δ.e+14).

4 is the number of bits in the table, 9 is the number of splines (coefficient pairs), and 5 is the degree of the fitted polynomial.

idx2 = 32 · (δ.e + 5 mod 27)
idx2 = idx2 + ZXt(TR(δ.m, Q−5) mod 32, 7)
idx2 = 1{δ.e = −1} ? 127 : idx2
(θ1, θ3, θ5) = GetC_{7,34,5,p,Q}(idx2, Θ2_sin, K2_sin)

In the interval $2^{-5}\le |\delta |<0.5$, a lookup table is used for differentiation based on the lower 2 bits of δ.e + 5 and the upper 5 bits of δ.m (this is the second innovation of the paper: segmented indexing) to call the corresponding (θ1, θ3, θ5) that minimizes the error. The case of $|\delta |=0.5$ is handled separately.

4. Use the Horner's method to calculate the corresponding floating-point value:

Δ = δ ⊗_{p,Q} δ
µ = ((θ5 ⊗ Δ) ⊞* θ3) ⊗ Δ
µ = (µ ⊞* θ1) ⊗ δ
Return (µ.z, a ⊕ α.s, Round*(µ.e,µ.m))

$\mathrm{\Delta }={\delta }^2$

$\mu =({\theta }_5\mathrm{\Delta }+{\theta }_3)\mathrm{\Delta }={\theta }_5{\delta }^4+{\theta }_3{\delta }^2$

$\mu =(\mu +{\theta }_1)\delta ={\theta }_5{\delta }^5+{\theta }_3{\delta }^3+{\theta }_1\delta \approx \sin \pi \delta$

As mentioned earlier, $\sin \pi \alpha =(-1{)}^{a\oplus 1\{\alpha <0\}}\sin \pi \delta$, so a ⊕ α.s determines the sign bit, and the final result is obtained by rounding.

To summarize, the ${\mathcal{F}}_{FP\sin \pi }^{8,23}$ function first performs range reduction on the input, reducing the problem to a small interval from 0 to 0.5 and recording the sign compensation; a fast path is used for extremely large or small inputs. Then, the function determines the segment based on the exponent and mantissa bits, selects the corresponding polynomial coefficients using a lookup table, calculates the approximate value using Horner's method, and finally restores the sign and rounds to a single-precision output.

One potential drawback of this method is that the table used by the GetC function is ad-hoc and differs from the protocol used for floating-point arithmetic operations. If one wants to arbitrarily specify $p,q$, or migrate to SecDouble, this coefficient table needs to be recalculated to ensure the error is less than 1 ULP. The paper sacrifices algorithmic flexibility in pursuit of performance and accuracy.

${\mathcal{F}}_{FP{\log }_2}^{8,23}$

Let $\alpha =m\cdot 2^N$, where $m\in [1,2)$ and $N=\alpha .e$. Let $a=1\{N=-1\}$. Then there are two cases:

• If $N\ne -1$, let $\delta =m-1$, then $\delta \in [0,1)$, and ${\log }_2\alpha ={\log }_{2}m+N={\log }_2(1+\delta )+N$.
• If $N=-1$, if $m\approx 2$, ${\log }_{2}m+N$ will approach zero, and the subtraction of two large numbers will affect the precision. Therefore, the author transforms the expression to ${\log }_2\alpha ={\log }_2(m/2)={\log }_2(1-(1-m/2))$. Let ${\delta }^{\prime }=1-m/2$, then ${\delta }^{\prime }\in (0,0.5]$, and then calculate ${\log }_2(1-{\delta }^{\prime })$. This avoids the error problem caused by subtracting two numbers.

$${\log }_2(\alpha )=\{\begin{array}{ll}N+{\log }_2(1+\delta )& a=0,\\ {\log }_2(1-{\delta }^{\prime })& a=1.\end{array}$$

Then, two sets of approximate polynomials $({\theta }_0^a,{\theta }_1^a,{\theta }_2^a,{\theta }_3^a)$ and $({\theta }_0^b,{\theta }_1^b,{\theta }_2^b,{\theta }_3^b)$ are constructed for $a=0$ and $a=1$ respectively. The values ​​of $\delta .e$ and $\delta .m$ within the specified range are then looked up in a table using the piecewise indexing method.

Next, the value of ${\log }_2(1+\cdot )$ is calculated using Horner's method. For the final addition of $N$, $N$ is first converted to a floating-point number using a lookup table, and then the ${\mathcal{F}}_{FPAdd}^{p,q}$ protocol is called.

1. Range Reduction Step:

a = 1{N = −1}
f = a ? (2^{q+1} − α.m) : (α.m − 2^q)
k,K = MSNZB(f); f = f *_{q+1} K
e = a ? (k − q − 1) : (k − q)

When $N=-1$ (in which case $a=1$), $f=1-m/2$; otherwise (in which case $a=0$), $f=m-1$, and then normalize $f$.

z = 1{f = 0}; e = (z ? −2^{p−1}+1 : e); 
N = α.e; δ = (z,0,e, f *_{Q+1} 2^{Q−q})

A floating-point number $\delta$ is constructed using $f$, and the precision is increased from $q=23$ bits to $Q=27$ bits, in preparation for the subsequent evaluation.

2. Polynomial Evaluation Step:

if 1{δ.z} then
   µ = Float_{p,Q}(0)

When $\delta =0$, ${\log }_2(1+\cdot )={\log }_{2}1=0$, so $\mu =0$ is returned.

if 1{δ.e < −5} then
   idx1 = (δ.e + 24) mod 2^5
   (θa0,θa1,θa2,θa3) = GetC_{5,19,4,p,Q}(idx1, Θ1_log, K1_log)
   (θb0,θb1,θb2,θb3) = GetC_{5,18,4,p,Q}(idx1, Θ3_log, K3_log)

When $2^{-24}\le \delta <2^{-5}$, the lower 5 bits of δ.e + 24 are used as the index to look up the table Θ1_log for the case $a=1$, and the table Θ3_log for the case $a=0$. Both lookups must be performed to avoid data dependencies.

else
   idx2 = 16 · (δ.e + 5 mod 2^7)
   idx2 = idx2 + ZXt(TR(δ.m, Q−4) mod 16, 7)
   (θa0,θa1,θa2,θa3) = GetC_{7,20,4,p,Q}(idx2, Θ2_log, K2_log)
   (θb0,θb1,θb2,θb3) = GetC_{7,32,4,p,Q}(idx2, Θ4_log, K4_log)

When $2^{-5}\le \delta <1$, use the lower 3 bits of δ.e + 5 and the upper 4 bits of δ.m as the index to look up the table Θ2_log for the case $a=1$, and the table Θ4_log for the case $a=0$.

(θ0,θ1,θ2,θ3) = a ? (θa0,θa1,θa2,θa3) : (θb0,θb1,θb2,θb3)

Based on the classification of the value of $a$ discussed above, select the final polynomial coefficients.

3. Horner's method and the final addition of $N$.

µ = ((θ3 ⊗ δ) ⊞* θ2) ⊗ δ
µ = ((µ ⊞* θ1) ⊗ δ) ⊞* θ0

Calculate the value of the cubic polynomial $\mu ={\theta }_3{\delta }^3+{\theta }_2{\delta }^2+{\theta }_1\delta +{\theta }_0={\log }_2(1+\cdot )$.

β = LInt2Float(N)
β′ = (β.z,β.s,β.e, β.m *_{Q+1} 2^{Q-6})

Using a small LUT (lookup table), $N$ is converted into a low-precision (6-bit mantissa) floating-point form $\beta$, which is then converted into a high-precision form $Q$, denoted as ${\beta }^{\prime }$.

γ = a ? µ : (µ ⊞* β′)
Return (γ.z, γ.s, Round*(γ.e, γ.m))

Finally, a floating-point addition is performed:

• If $a=0$, then $\gamma =\mu +{\beta }^{\prime }={\log }_2(1+\cdot )+N$,
• If $a=1$, then $\gamma =\mu ={\log }_2(1-\cdot )$.

The final result of the protocol is obtained by rounding $\gamma$.