From a LeetCode problem to a discrete logarithm solution algorithm

Let's first look at the problem statement. You can think about it before clicking in:

Given an array of integers nums containing $n+1$ integers where each integer is in the range $[1,n]$ inclusive, $n\le {10}^5$.

There is only one repeated number in nums, return this repeated number.

You must solve the problem without modifying the array and using only constant extra space.

Algorithm Solution Explanation

Without considering the third constraint, any $O(n\log n)$ sorting algorithm would suffice for this problem. Even without the $O(1)$ space restriction, since the elements are in the range $[1,n]$, bucket sort could also achieve AC. However, if we are not allowed to modify the array nums or create a new array, then a two-pointer approach must be considered.

A relatively straightforward method is binary search. Given that the value range is $[1,n]$, we can set $mid=\lfloor \frac{1+n}{2}\rfloor$ and count the number of elements in nums that are $\le mid$ (denoted as $x$). If $x\le mid$, we can prove that there are no duplicate elements in $[1,mid]$:

Here, we use proof by contradiction. Let $[condition]$ be $1$ when "condition" is true and $0$ otherwise.

Assume there exists a duplicate element in $[1,mid]$ and $\sum _{i=1}^n[nu{m}_i\le mid]=x$. Since there is only one duplicate element, the elements in $[mid+1,n]$ can only appear $0$ or $1$ times. Therefore, $\sum _{i=1}^n[nu{m}_i>mid]\le n-mid$. Adding the two expressions gives $n+1\le x+n-mid\le n$, which is a contradiction!

Hence, the assumption is false, and the original conclusion is correct: there are no duplicate elements in $[1,mid]$.

With the above conclusion, we can assert that when $x\le mid$, we should continue searching in $[mid+1,n]$. Conversely, when $x>mid$, by the pigeonhole principle, it is evident that there must be a duplicate element in $[1,mid]$, and we should continue searching in $[1,mid]$.

This process is performed recursively, with an overall time complexity of $O(n\log n)$.

def findDuplicate(self, nums: List[int]) -> int:
    low, high = 1, len(nums) - 1
    
    while low < high:
        mid = (low + high) // 2
        count = 0
        for num in nums:
            if num <= mid:
                count += 1
        if count > mid:
            high = mid
        else:
            low = mid + 1
            
    return low

Floyd's Cycle-Finding Algorithm

But there is a follow-up in the problem:

Can you solve the problem in linear runtime complexity?

This is where binary search falls short. Here, I chose to give up and learned about an algorithm called Floyd's cycle-finding algorithm, also known as the tortoise and hare algorithm. The process is as follows:

First, construct a graph from the nums array. The index of the array is one endpoint (here, the index starts from 1), and the value at that index is the endpoint it points to. For example, the following array:

[5,3,1,6,2,5]

Corresponds to the following directed graph:

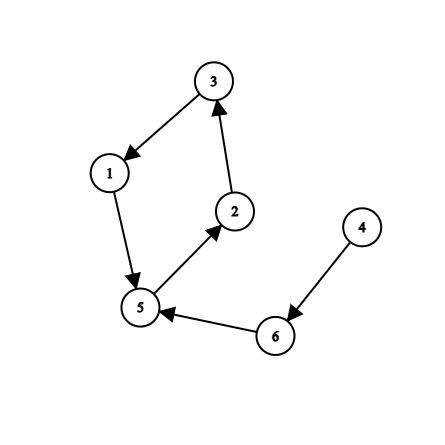
First, the hare and the tortoise start from a randomly chosen point (for demonstration purposes, we choose point 4). The hare moves faster, taking two steps at a time, while the tortoise moves slower, taking one step at a time. This leads to the following scenario (left: hare, right: tortoise):

4 4
5 6
3 5
5 2
3 3

At this point, the hare and the tortoise meet, indicating that the algorithm has successfully found a cycle (otherwise, the hare would always be ahead of the tortoise).

The next step of the algorithm is to find the "starting point" of the cycle (which is point 5. If they started inside the cycle, that would naturally be the starting point). The tortoise is moved back to the starting point 4, while the hare remains at its current position 3. Then, both move one step at a time:

3 4
1 6
5 5

It can be observed that they meet at the "starting point" of the cycle, point 5. It can be proven that, regardless of the shape of the graph, they will always meet at the "starting point" of the cycle:

Let the circumference of the cycle be $C$, and the length of the tail (i.e., the path 5->6->4 in the graph) be $d$. When they first meet, the hare has taken $2t$ steps, and the tortoise has taken $t$ steps. Clearly, we have $C|(2t-t)$. When the tortoise is moved back to the starting point, since they now move at the same speed, the distance between the hare and the tortoise remains constant at $2t$. When the tortoise takes $d$ steps to reach the "starting point", the hare takes $2t+d$ steps. Since $C|2t$, the hare and the tortoise must meet, and they do so at the "starting point".

The final step of the algorithm is to keep the hare stationary while the tortoise moves around the cycle to measure the circumference $C$, thus concluding the algorithm.

Returning to the problem, since there is only one duplicate number, it must be the "starting point" itself. Therefore, we only need to perform the first two steps of the algorithm to get AC. The time complexity is $O(n)$.

def findDuplicate(self, nums: List[int]) -> int:
    slow = nums[0]
    fast = nums[0]
    while True:
        slow = nums[slow]
        fast = nums[nums[fast]]
        if slow == fast:
            break
    fast = nums[0]
    while slow != fast:
        slow = nums[slow]
        fast = nums[fast]
    return fast

Brent's Algorithm

Brent improved upon Floyd's cycle-finding algorithm by using powers of two step sizes (power) to detect cycles. It introduces lambda (which increments with each iteration and can be understood as the cycle length $C$) and mu (which increments to eventually determine the tail length $d$). The algorithm has two main advantages:

• It directly finds the cycle length $C$ in the first step.
• Each iteration requires only one computation of $f$, compared to Floyd's three.

For example, consider the following graph (assuming all nodes start from 1):

1 -> 2 -> 3 -> 4 -> 5 -> 3

We then have:

• Frame 1: Tortoise at 1, Hare at 2, power = 1, lambda = 1.
• Frame 2: Tortoise at 2, Hare at 3, power = 2, lambda = 1.
• Frame 3: Tortoise at 2, Hare at 4, power = 2, lambda = 2.
• Frame 4: Tortoise at 4, Hare at 5, power = 4, lambda = 1.
• Frame 5: Tortoise at 4, Hare at 3, power = 4, lambda = 2.
• Frame 6: Tortoise at 4, Hare at 4, power = 4, lambda = 3 (cycle length detected).
• Frame 7: Tortoise at 1, Hare at 1 (reset for finding position of length lambda).
• Frame 8: Tortoise at 1, Hare at 2.
• Frame 9: Tortoise at 1, Hare at 3.
• Frame 10: Tortoise at 1, Hare at 4. (repeated lambda times)
• Frame 11: Tortoise at 2, Hare at 5, mu = 1.
• Frame 12: Tortoise at 3, Hare at 3, mu = 2. (cycle start found)

Python code is as follows:

def brent(f, x0) -> (int, int):
    """Brent's cycle detection algorithm."""
    # main phase: search successive powers of two
    power = lam = 1
    tortoise = x0
    hare = f(x0)  # f(x0) is the element/node next to x0.
    # this assumes there is a cycle; otherwise this loop won't terminate
    while tortoise != hare:
        if power == lam:  # time to start a new power of two?
            tortoise = hare
            power *= 2
            lam = 0
        hare = f(hare)
        lam += 1

    # Find the position of the first repetition of length λ
    tortoise = hare = x0
    for i in range(lam):
    # range(lam) produces a list with the values 0, 1, ... , lam-1
        hare = f(hare)
    # The distance between the hare and tortoise is now λ.

    # Next, the hare and tortoise move at same speed until they agree
    mu = 0
    while tortoise != hare:
        tortoise = f(tortoise)
        hare = f(hare)
        mu += 1
 
    return lam, mu

pollard_rho

Since this graph structure easily brings to mind the Greek letter $\rho$, and coincidentally, Pollard himself thought the same way. He identified an algebraic structure: a finite ring $R_n$, and then introduced an operation $f(x)=(x^2+t)\mathrm{mod}n$ to generate a pseudorandom sequence $A=[x,f(x),f^2(x),\cdots ]$. If $n=pq$, we assume this random sequence is uniformly distributed in $[A_i\mathrm{mod}p]$. According to the birthday paradox, we expect to find a pair of identical values within $O(\sqrt{p})$ time.

However, we do not know the value of $p$ in advance, so we need to determine whether $gcd(|A_i-A_j|,N)\ne 1$. This is because if $A_i\equiv A_j\mathrm{mod}p$, then clearly $|A_i-A_j|$ is a multiple of $p$, and thus $gcd(|A_i-A_j|,N)$ is not equal to 1.

So how do we traverse the indices $i,j$ (hare and tortoise)? Although the sequence $A$ is modulo $n$, considering $A_i\mathrm{mod}p$ and $A_j\mathrm{mod}p$, since $F_p$ is a field, repeatedly applying the function $f$ to an element will eventually form a cycle (or "orbit"). In this case, Floyd's cycle-finding algorithm becomes useful. After a finite number of iterations, $i$ and $j$ may first meet in $F_p$, returning $p$ as the result. Similarly, they may first meet in $F_q$, returning $q$ as the result. Alternatively, they might meet in $R_n$ and return $n$, but this result is trivial, requiring the algorithm to be restarted.

This algorithm is called the Pollard's rho algorithm for primality testing. Since, in the worst case, $p$ is $O(\sqrt{n})$, the average time complexity of Pollard's rho is $O(n^{1/4})$.

from math import *

def f(x, c, n):
    return (x * x + c) % n

def pollard_rho(n, max_attempts=10):
    if n % 2 == 0:
        return 2                    # tackle even case
    
    for attempt in range(max_attempts):
        x = random.randint(1, n-1)  # tortoise
        y = x                       # hare
        c = random.randint(1, n-1)  # c of f(x)
        g = 1                       # GCD result

        # Floyd's cycle-finding
        while g == 1:
            x = f(x, c, n)          # tortoise takes 1 step
            y = f(f(y, c, n), c, n) # hare takes 2 steps
            g = gcd(abs(x - y), n)  # calculate gcd

        if 1 < g < n:
            return g                # non-trivial divisor
        # retry
        
    return n                        # max retries exceeded

Pollard's Rho Using Brent's Method

In order to hastily write a paper, Brent also replaced Floyd's cycle-finding method in Pollard's Rho with his own algorithm and experimentally demonstrated that his cycle detection method is 36% more efficient than Floyd's, resulting in an overall performance improvement of 24%.

The code won't be posted here, but one possible implementation can be found at:

https://comeoncodeon.wordpress.com/2010/09/18/pollard-rho-brent-integer-factorization/

Pollard's Rho for DLP

Just as it is natural to associate the prime factorization problem with the DLP (Discrete Logarithm Problem), Pollard himself extended the methodology of his rho algorithm—originally applied to factor integers in finite rings $R_n$—to tackle the DLP.

Suppose we aim to solve the discrete logarithm problem ${\alpha }^{\gamma }=\beta (\mathrm{mod}n)$, where $n$ is prime. We seek values $a,b,A,B$ such that ${\alpha }^a{\beta }^b={\alpha }^A{\beta }^B$. Substituting the original equation, we have:

$${\alpha }^a{\alpha }^{\gamma b}={\alpha }^A{\alpha }^{\gamma B}$$

By Euler's theorem, this implies:

$$a+\gamma b\equiv A+\gamma B(\mathrm{mod}n-1)$$$$(B-b)\gamma \equiv a-A(\mathrm{mod}n-1)$$

We can then solve for $\gamma$ using the extended Euclidean algorithm (exgcd).

The key challenge lies in finding such $a,b,A,B$. This requires selecting a mapping ${\mathbb{F}}_n\to {\mathbb{F}}_n$ (analogous to the earlier $f(x)=x^2+t\mathrm{mod}n$) such that the sequence $x_i={\alpha }^{a_i}{\beta }^{b_i}$ is sufficiently uniformly distributed over ${\mathbb{F}}_n$. Pollard proposed one such mapping, though he did not rigorously prove its uniformity:

$$f(x)=\{\begin{array}{ll}\alpha x,& \text{if }0\le x<p/3,\\ x^2,& \text{if }p/3\le x<2p/3,\\ \beta x,& \text{if }2p/3\le x<p.\end{array}$$

Here, we use a variant of this formula:

$$f(x)=\{\begin{array}{ll}{x}^2,& \text{if }x\equiv 0\mathrm{mod}3,\\ \alpha x,& \text{if }x\equiv 1\mathrm{mod}3,\\ \beta x,& \text{if }x\equiv 2\mathrm{mod}3.\end{array}$$

We initialize the tortoise as $x=1,a=0,b=0$, and the hare as $X=x,A=a,B=b$, constructing the pseudorandom sequence $A=[1,f(x),f^2(x),\cdots ]$. Floyd's cycle-finding algorithm is then applied: we compute $X=f^2(X)$ and $x=f(x)$ in each step. The corresponding exponents $a,b,A,B$ are updated accordingly (as you, the astute reader, may infer). After a finite number of iterations, a collision ${\alpha }^a{\beta }^b={\alpha }^A{\beta }^B$ is found.

Below is an example for $n=1019,\alpha =2,\beta =5$. Each row shows the result of one iteration for $x$ and two iterations for $X$:

 i     x   a   b     X   A   B
------------------------------
 1     2   1   0    10   1   1
 2    10   1   1   100   2   2
 3    20   2   1  1000   3   3
 4   100   2   2   425   8   6
 5   200   3   2   436  16  14
 6  1000   3   3   284  17  15
 7   981   4   3   986  17  17
 8   425   8   6   194  17  19
..............................
48   224 680 376    86 299 412
49   101 680 377   860 300 413
50   505 680 378   101 300 415
51  1010 681 378  1010 301 416

A collision occurs when $a,b,A,B=681,378,301,416$. Substituting into $(B-b)\gamma \equiv a-A(\mathrm{mod}n-1)$, we get $38\gamma \equiv 380$, yielding $\gamma =10$ or $519$ (discarded).

Thus, a collision is found in approximately $\frac{\sqrt{\tau n}}{2}$ steps (where $\tau =2\pi$), though a formal proof is lacking. The algorithm has a complexity of $O(\sqrt{n})$, matching that of the deterministic Baby-Step Giant-Step (BSGS) algorithm.

Combining DLP with the Pohlig-Hellman Algorithm

The Pohlig-Hellman algorithm can also be used to efficiently solve the Discrete Logarithm Problem (DLP). The main idea is to factorize $n-1$ into its prime factors, then use a certain algorithm (the linked article uses BSGS) to solve the discrete logarithm in $\mathrm{GF}(p)$, and finally combine the results for each prime $p$ using the Chinese Remainder Theorem (CRT). A detailed introduction is well-written by Ruan Xingzhi, which you can refer to:

https://www.ruanx.net/pohlig-hellman/

If the prime factorization of $n-1$ in the DLP is known, this algorithm can be combined with the previous Pollard's rho algorithm to reduce the time complexity of solving the DLP from $O(\sqrt{n})$ (as in the Pollard's rho version for DLP) to $O(\sqrt{p})$, where $p$ is the largest prime factor of $n-1$.

Therefore, in summary, the difficulty of the DLP depends on whether $n-1$ is smooth. For a general $n$ (such as a large prime), the time complexity is $O(\sqrt{n})$ using Pollard's rho or BSGS. If $n$ is factorized as $\prod p_i^{e_i}$, the time complexity becomes $O(\sum e_i\sqrt{p_i})$.

Reference Materials

An Introduction to Mathematical Cryptography

https://www.youtube.com/watch?v=pKO9UjSeLew

https://leetcode.com/problems/find-the-duplicate-number/solutions/4916414/c-2-optimal-approaches-o-n-and-o-nlogn-constant-space/

https://www.ruanx.net/pohlig-hellman/

https://en.wikipedia.org/wiki/Pollard's_rho_algorithm_for_logarithms

https://en.wikipedia.org/wiki/Pollard's_rho_algorithm

https://en.wikipedia.org/wiki/Pohlig–Hellman_algorithm

https://en.wikipedia.org/wiki/Cycle_detection#Brent.27s_algorithm

https://comeoncodeon.wordpress.com/2010/09/18/pollard-rho-brent-integer-factorization/

http://wwwmaths.anu.edu.au/~brent/pd/rpb051i.pdf