How to calculate square roots by hand

In elementary school, my father proudly showed me how he had learned to manually calculate square roots during his school days, saying it might come in handy for showing off among friends someday. I probably learned it back then, but later, this method seemed to disappear from math textbooks. All I could recall was the mnemonic: "twenty times the initial quotient plus the next quotient." The main purpose of this article is to recount the process of how I managed to recall it.

Chunking

First, I chose the number 167 for testing:

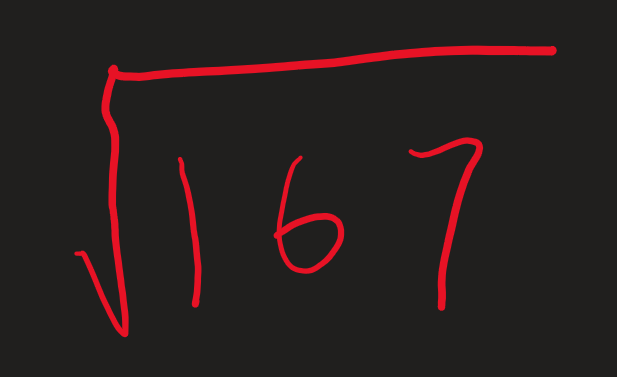
A rough estimate shows that the answer lies between 12 and 13. However, there are three blank spaces above the vertical calculation, while the quotient has only two digits. So, I need to figure out where these two digits should be placed.

In other words, should I use 16 to perform the "twenty times the initial quotient plus the next quotient" operation, or should I use 1?

Clearly, the first digit, 1, should be written in the highest position. But does this apply to all numbers? So, I changed 167 to 67:

The answer lies between 8 and 9. In this case, if I perform the operation on the higher digit 6, the result would start with 2, which is obviously incorrect. Therefore, I assume that the grouping is likely based on the units digit, with operations performed in pairs of two digits. (Since the square of a single-digit number can "occupy" a two-digit space, and the square of a two-digit number can "occupy" a four-digit space, it makes sense to group them in pairs of two.)

What Are the Initial Quotient and the Secondary Quotient?

Let's return to the previous number, 167. First, we take the square root of the hundreds place:

At this point, the value of "?" should be 2. Then, the value of "twenty times the initial quotient plus the secondary quotient" is $20 \times 1 + 2 = 22$ , and $22 \times 2 = 44 < 67$ , which is very reasonable.

Now, I notice:

(20 \times 1 + 3) \times 3 = 69

And since $169 = 13^{2}$ , I understand that the constant $20$ is likely related to the decimal system and the square sum formula.

Thus, we can prove the correctness of the algorithm. Let the initial quotient be $a$ and the secondary quotient be $b$ . Then:

(10 a + b)^{2} = 100 a^{2} + 20 a b + b^{2} = 100 a^{2} + (20 a + b) b

Q.E.D.

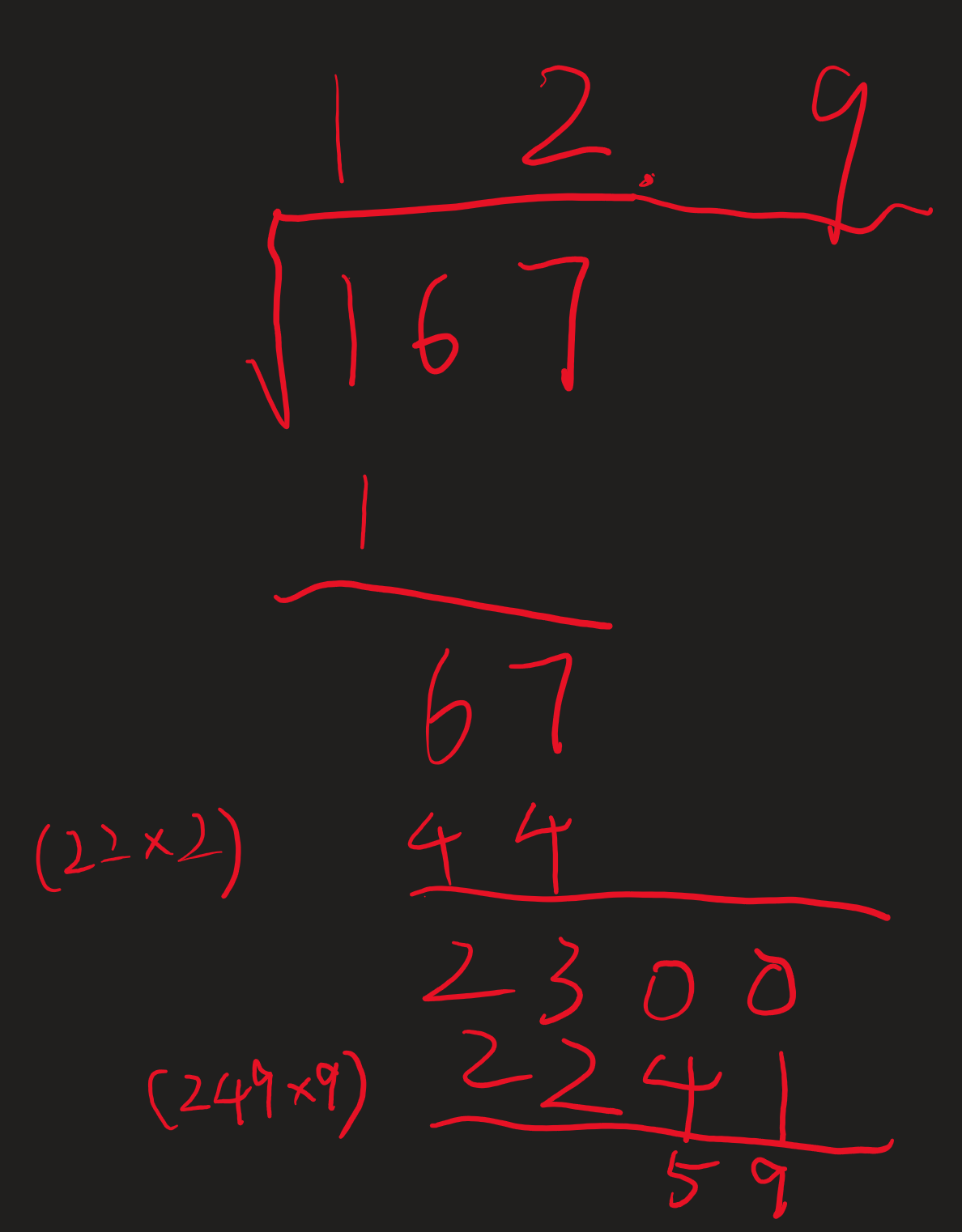
This simultaneously explains the principle of "twenty times the initial quotient plus the secondary quotient" and the grouping of digits in pairs. Here, the secondary quotient $b$ is clearly the digit we are currently calculating, and we can infer that the initial quotient $a$ should be the value of the quotient computed earlier. Let's proceed with the calculation:

Using a calculator, the answer is 12.9228, confirming the algorithm's correctness. If we take the previous result $2 \times 20 = 40$ , even $49 \times 9$ is far less than $2300$ , so the conjecture is correct.

Writing a Program

Obviously, manual verification is time-consuming and laborious. If we can speed up test case validation by writing a program, it can further enhance our confidence in the algorithm. So, we first write the function for "twenty times the initial quotient plus the next digit":

def _20_p1(first, rem, next):
    """
    recursively tries largest x from 0 to 9 to get
    (20 * first + x) * x <= rem * 100 + next
    return x and remainer
    """
    x = 0

    for i in range(11):
        if (20 * first + i) * i > rem * 100 + next:
            x = i - 1
            break
        assert i != 10
    
    return (x, rem * 100 + next - (20 * first + x) * x)

Here, first refers to the "initial quotient"; rem refers to the current remainder, such as "0", "23", "59" in the previous example; and next refers to the next digit, such as "67", "0".

Then, we try to manually use _20_p1 to simulate the previous algorithm logic. We temporarily skip the obvious first step of obtaining $1$ and directly simulate the process of obtaining the second digit $2$ :

prev, modulo = 1, 0
prev, modulo = prev * 10 + _20_p1(prev, modulo, 67)[0], _20_p1(prev, modulo, 67)[1]
print(_20_p1(prev, modulo, 0))

Previously, we obtained the "initial quotient" prev as $1$ , and rem (i.e., modulo in the code) as $0$ . Then, we used _20_p1(prev, modulo, 67) to get the "next digit" and remainder for this round of "twenty times the initial quotient plus the next digit", represented by the suffixes [0] and [1], respectively.

The "initial quotient" for this round is merged with the current "next digit" by multiplying by $10$ to become the "initial quotient" for the next round, while the remainder becomes the new modulo variable for the next round's _20_p1(prev, modulo, 00), multiplied by $10$ and added to 00, starting a new iteration.

The final question is: how do we obtain the next variable? The answer is simple: treat the dividend as a string, split it into chunks of two digits each, and then convert it back.

Thus, a recursive process is formed. The boundary condition (the initial square root extraction) is also straightforward: simply set the initial quotient and modulo to $0$ :

res = ''
chunks = split_two_by_two(raw_number, int_digit % 2)

# now do the algorithm
prev, modulo = 0, 0
for i in range(iters):
    if i < len(chunks):
        next_chunk = int(chunks[i])
    else:
        next_chunk = 0

    x, rem = _20_p1(prev, modulo, next_chunk)
    prev, modulo = prev * 10 + x, rem
    res = str(prev)

Let's briefly calculate the complexity. Assuming the number is $m$ , the process of _20_p1 is related to the number of digits of $m$ , i.e., $O (\log m)$ . Each iteration also computes one digit. Assuming we stop at the integer part, the complexity is also $O (\log m)$ . Therefore, the total time complexity is $O (\log^{2} m)$ .

This time complexity is even worse than using the binary method, which has a time complexity of $O (\log m)$ . So, the "twenty times the initial quotient plus the next digit" method can only be used to show off in front of friends.

Complete Code

After some simple debugging and special case handling, I have written code with a certain level of robustness that passes a series of test cases. Therefore, I am sharing it below:

Note: The input must be a natural number; support for decimals has not been implemented yet (though it would just involve a lot of detailed processing).

def _20_p1(first, rem, next):
    """
    recursively tries largest x from 0 to 9 to get
    (20 * first + x) * x <= rem * 100 + next
    return x and remainer
    """
    x = 0

    for i in range(11):
        if (20 * first + i) * i > rem * 100 + next:
            x = i - 1
            break
        assert i != 10
    
    return (x, rem * 100 + next - (20 * first + x) * x)

def getintdigit(x):
    return len(str(x))

def split_two_by_two(s, first_len):
    if first_len == 0:
        first_len += 2
    if first_len >= len(s):
        return [s]

    first_chunk = s[:first_len]
    remaining = s[first_len:]
    
    rest_chunks = [remaining[i:i+2] for i in range(0, len(remaining), 2)]
    
    return [first_chunk] + rest_chunks

def mysqrt(x, iters):
    """
    Returns the square root of x.
    iters means keep {iters} valid digits.
    """
    if not isinstance(iters, int) or (iters < 1):
        raise ValueError('iters must greater than 0')
    if not isinstance(x, int):
        raise ValueError('x must be an integer')
    if x < 0:
        raise ValueError('x must be non-negative')

    int_digit = getintdigit(x)
    res_int_digit = (int_digit - 1) // 2 + 1

    raw_number = str(x).replace(".", "")
    res = ''
    chunks = split_two_by_two(raw_number, int_digit % 2)

    # now do the algorithm
    prev, modulo = 0, 0
    for i in range(iters):
        if i < len(chunks):
            next_chunk = int(chunks[i])
        else:
            next_chunk = 0

        x, rem = _20_p1(prev, modulo, next_chunk)
        prev, modulo = prev * 10 + x, rem
        res = str(prev)

    if iters <= res_int_digit:
        return res + '0' * (res_int_digit - iters)
    return res[:res_int_digit] + '.' + res[res_int_digit:]

print(mysqrt(167, 10))