Is there really a bad tune in Mahjong Soul?

This article will conduct several small experiments to verify the randomness and fairness of Mahjong Soul.

Problem Analysis

Since Mahjong Soul does not enforce mandatory paid features, it does not have a stable revenue source like Tenhou (Phoenix Table). As a commercial company, the developer, Cat Food Studio, aims to generate income by attracting users. Therefore, tampering with the wall to control user wins and losses is a common business tactic, as it can manipulate user emotions to some extent, thereby increasing user retention and the potential for impulsive spending. This behavior of "tampering with the wall to control user wins and losses" is widely referred to by players as "恶调" (evil tuning).

Mahjong Soul has stated in its announcements that "Mahjong Soul guarantees completely random generation of game rounds. The wall sequence is fixed at the start of the round, with no targeted dealing and no tampering with the wall during the game." To support this claim, Mahjong Soul introduced MD5 encryption before May 24, 2023, SHA256 encryption after May 24, 2023, and upgraded to salted SHA256 encryption on February 28, 2024.

Based on knowledge from a sophomore-level cryptography course, MD5/SHA256 currently ensures that, given a specific wall and its corresponding hash value, one cannot tamper with the wall to produce the same hash value. Salted SHA256 only increases the difficulty of tampering (as there is no rainbow table to reference).

By the way, this type of attack is known as a second pre-image attack. Although Wang Xiaoyun et al. proposed a collision attack method for MD5 in 2004³, there is currently no literature proposing a second pre-image attack method for MD5⁴. Therefore, MD5 is still temporarily secure in this context.

Thus, after Mahjong Soul upgraded to salted SHA256 encryption, it can only corroborate that the wall sequence is fixed at the start of the round and that there is no tampering with the wall during the game, but it cannot prove completely random generation of game rounds or no targeted dealing.

The following content of this article will focus on verifying the two claims: "completely random generation of game rounds" (randomness) and "no targeted dealing" (fairness).

Experimental Design

The author speculates that "evil tuning" behavior might be achieved by tampering with the wall during dealing. There are two main possible methods:

Creating a significant disparity in the shanten count of each player's starting hand.
Placing the tiles needed by certain players at the very end of the wall, making it difficult for them to draw those tiles.

We can verify the fairness of Mahjong Soul through the following experiments:

Calculate the shanten count of each player at the end of the dealing phase and check for significant disparities.
Assuming each player follows pure tile efficiency, calculate the shanten count of all four players at each turn and create bar charts to check for significant disparities.
Calculate the ready-hand rate of each player over several rounds and check for significant disparities.

We can verify the randomness of Mahjong Soul through the following experiment:

Compare these data with Tenhou, which publicly discloses its wall generation algorithm, and check for significant disparities between the two.

Data Collection

The author extracted some records from their own game logs in Mahjong Soul and Tenhou, listed below (to ensure fair sampling, a second-place hanchan, a fourth-place hanchan, and a fourth-place tonpu were selected from both platforms):

https://tenhou.net/0/log/find.cgi?log=2024081216gm-0009-0000-bfc28ebf&tw=x

https://tenhou.net/0/log/find.cgi?log=2024081415gm-0009-0000-22c53785&tw=x

https://tenhou.net/0/log/find.cgi?log=2024081914gm-0001-0000-f25dab62&tw=x

https://game.maj-soul.com/1/?paipu=jmjsmq-v4x15u70-xd4c-69hi-h8cn-lfnuplvsqzpr_a229216253_2

https://game.maj-soul.com/1/?paipu=jmjsmq-2ty0y7z7-3db5-6gag-gihp-iomhjkrnryry_a229216253_2

https://game.maj-soul.com/1/?paipu=jmjsmp-r4wt5744-3cbe-6g5c-hmbi-gqhsqliloqpo_a229216253_2

To facilitate data processing, relevant code² was used and slightly modified to convert Tenhou's wall into Mahjong Soul's wall format.

#!/usr/bin/python3
import hashlib
import base64
import re
import gzip
import random
import sys

def _get_seed_from_plaintext_file(file):
    text = file.read()
    match_str = re.search('seed=.* ref', text).group()
    begin_pos = match_str.find(',') + 1
    end_pos = match_str.rfind('"')
    return match_str[begin_pos:end_pos]

def get_seed_from_file(filename):
    GZIP_MAGIC_NUMBER = b'\x1f\x8b'
    f = open(filename, 'rb')
    if f.read(2) == GZIP_MAGIC_NUMBER:
        f.close()
        f = gzip.open(filename, 'rt')
    else:
        f.close()
        f = open(filename, 'r')
    return _get_seed_from_plaintext_file(f)

def seed_to_array(seed_str):
    seed_bytes = base64.b64decode(seed_str)
    result = []
    for i in range(len(seed_bytes) // 4):
        result.append(int.from_bytes(seed_bytes[i*4:i*4+4], byteorder='little'))
    return result

N = 624
mt = [0] * N
mti = N + 1
def init_genrand(s):
    global mt
    global mti
    mt[0] = s & 0xffffffff
    mti = 1
    while mti < N:
        mt[mti] = (1812433253 * (mt[mti-1] ^ (mt[mti-1] >> 30)) + mti)
        mt[mti] &= 0xffffffff
        mti += 1

def init_by_array(init_key, key_length):
    global mt
    init_genrand(19650218)
    i = 1
    j = 0
    k = (N if N > key_length else key_length)
    while k != 0:
        mt[i] = (mt[i] ^ ((mt[i-1] ^ (mt[i-1] >> 30)) * 1664525)) + init_key[j] + j # non linear
        mt[i] &= 0xffffffff
        i += 1
        j += 1
        if i >= N:
            mt[0] = mt[N-1]
            i = 1
        if j >= key_length:
            j = 0
        k -= 1
    k = N - 1
    while k != 0:
        mt[i] = (mt[i] ^ ((mt[i-1] ^ (mt[i-1] >> 30)) * 1566083941)) - i # non linear
        mt[i] &= 0xffffffff
        i += 1
        if i>=N:
            mt[0] = mt[N-1]
            i = 1
        k -= 1
    mt[0] = 0x80000000

haiDisp = ["1m", "2m", "3m", "4m", "5m", "6m", "7m", "8m", "9m", "1p", "2p", "3p", "4p", "5p", "6p", "7p", "8p", "9p", "1s", "2s", "3s", "4s", "5s", "6s", "7s", "8s", "9s", "1z", "2z", "3z", "4z", "5z", "6z", "7z"]

def gen_yama_from_seed(seed_str):
    seed_array = seed_to_array(seed_str)
    init_by_array(seed_array, 2496/4)
    #print(mt[623])
    mt_state = tuple(mt + [624])
    random.setstate((3, mt_state, None))
    for nKyoku in range(10):
        rnd = [0] * 144
        rnd_bytes = b''
        src = [random.getrandbits(32) for _ in range(288)]
        #print(src[0])
        for i in range(9):
            hash_source = b''
            for j in range(32):
                hash_source += src[i*32+j].to_bytes(4, byteorder='little')
            rnd_bytes += hashlib.sha512(hash_source).digest()
        for i in range(144):
            rnd[i] = int.from_bytes(rnd_bytes[i*4:i*4+4], byteorder='little')
        # till here, rnd[] has been generated
        yama = [i for i in range(136)]
        for i in range(136 - 1):
            temp = yama[i]
            yama[i] = yama[i + (rnd[i]%(136-i))]
            yama[i + (rnd[i]%(136-i))] = temp
        # print('nKyoku=' + str(nKyoku) + ' yama=')
        for i in range(135, -1, -1):
            print(haiDisp[yama[i] // 4], end='')
        print('')

def test_mt_init():
    init_genrand(19650218)
    mt_state = tuple(mt + [624])
    random.setstate((3, mt_state, None))
    print(random.getrandbits(32))


if __name__ == "__main__":
    #test_mt_init()
    filename = sys.argv[1]
    seed_str = get_seed_from_file(filename)
    gen_yama_from_seed(seed_str)

By adding the player's position in front of the wall code, we can obtain experimental data similar to the following:

W 4z1z9m2m0s6m2s1z9p8s7p7z2s1p6m7p8p0p1s4z7s7z8p3p9m4s4z2z4s7m3z1m9m6z3s8m3m2m4p5p7m1s1m3m5z2p4p2p3s2z6m6p4m1s5p7z7p4p4m6z1p6m8p8m5z6s9p1m9s9p6s7s4m5s6p3z9p3z2m1p4m3s2s6p1z7s9m4s8p9s2p5z4p6z2z3p3s7s6z8m8s1p3p5z4s7m6s5p5s3m7z0m2m3p2z9s8s8s6s1m1z2s2p1s4z8m5m7p7m3m6p3z9s5s5m5m
S 7s5z1p4s1z4z9s8p6s9p3m1z5z8m7z1m4z9m3z6p4m7p2s5m5p7s8s1s1s7s4p8m9m3p3m1m1p8s6s9s6p6z8s3z3s9s4m4s1z6s2z5s6m4p9m2p7z2s2z5p9m9p2z7m2m2m6z1s5p2p8p6p6s3s4p1p5m3p7m7z2m0p0s3m0m6m9p7p3m7s4s2p5m1m3z3z6m1m4z2s2p6m8p7m2s5z3p8m9s3p2z9p4m3s7p6z8p6z7z1s5s6p4p5z2m1z3s4s7p7m4m8s1p5s4z8m
E 5p0s2z7s2z8m7m9p3s6m5z1z3p5p2m5z3m3s7m9p4s6s8p8p1z2s3s3z6z9m4m1m5s4s8s9p1z1s1p2p6p3z8s0m2s4s6z9s2p8m4m8p7s1s1p1m6s6s7p4p2s5m3p5s5p8m6m7z8m8s4p6p9s7m6p3z4p2s1p2m7p1s2m3z4z2p6s6z6p1s8p8s9s7z1z7z7s5m9m7p3p5s5z2z5z1m7z3m3p4m0p2m1p9p6m4m2p5m9m9m6z2z4z4z3m4p1m9s4s7m7p6m3s3m7s4z
...

Experimental Process

Experiment 1: Verifying Whether There Is a Gap in Initial Shanten Count

There are existing tools¹ for calculating the shanten count of a known hand, which we can directly use.

Below is the author's reference code:

#include <iostream>
#include <vector>
#include <assert.h>
#include <fstream>
#include "calsht.hpp"

// Function to convert a character to a numerical index
int charToIndex(char ch) {
    if (ch >= '1' && ch <= '9') return ch - '1';
    if (ch == '0') return 4;
    std::cout << "Error: invalid character" << std::endl;
    exit(0);
}

// Deal four consecutive tiles to each player for three rounds, then deal one tile to East, South, West, and North
int cal_offset(char player_position, int seq) {
    int offset = 0;
    if (player_position == 'S') {
        offset = 1;
    } else if (player_position == 'W') {
        offset = 2;
    } else if (player_position == 'N') {
        offset = 3;
    }

    if (seq < 12) {
        int round = seq / 4;
        return round * 16 + offset * 4 + seq % 4;
    } else if (seq == 12) {
        return 48 + offset;
    }
    assert(-1);
    return -1;
}

// Function to return the player's hand vector based on the input tile string and player position
std::vector<int> parseHand(const std::string& tiles, char player_position) {
    std::vector<int> hand(34, 0);  // 34 elements, initialized to 0 (9 Man + 9 Pin + 9 Sou + 7 Honor tiles)
    
    for (int i = 0; i < 13; ++i) {
        char ch1 = tiles[cal_offset(player_position, i) * 2];   // First character is a digit
        char ch2 = tiles[cal_offset(player_position, i) * 2 + 1]; // Second character is a letter m/p/s/z

        int index = charToIndex(ch1);
        if (ch2 == 'm') hand[index]++;         // Manzu
        else if (ch2 == 'p') hand[9 + index]++; // Pinzu
        else if (ch2 == 's') hand[18 + index]++; // Souzu
        else if (ch2 == 'z') hand[27 + index]++; // Honor tiles
    }

    return hand;
}

int main(int argc, char* argv[])
{
    Calsht calsht;

    // Set the location of shanten tables
    calsht.initialize(".");


    std::ifstream file(argv[1]); // Open the file
    std::string line;

    if (file.is_open()) {
        while (std::getline(file, line)) {  // Read line by line
            if (!line.empty()) {            // Check if it's not an empty line
                // std::cout << line << std::endl;
                std::vector<char> player_position = {'E', 'S', 'W', 'N'};
                char direction = line[0];
                std::string tiles = line.substr(2);

                for (auto p : player_position) {
                    std::vector<int> hand = parseHand(tiles, p);

                    auto [sht, mode] = calsht(hand, 4, 7);

                    // std::cout << "Player position: " << p << std::endl;
                    std::cout << sht - 1 << " ";
                }
                std::cout << " " << direction;
                std::cout << std::endl;
            }
            else {
                std::cout << std::endl;
            }
        }
        file.close();  // Close the file
    } else {
        std::cerr << "Unable to open file" << std::endl;
        return 1;
    }
    return 0;
}

By substituting the previously obtained Majsoul input, we can get the following results:

To facilitate the calculation of the average shanten count, I shifted each column so that each player corresponds to a fixed column, with the author corresponding to the first column.

Using Python's matplotlib library, we can generate the following line chart:

The following sample code does not perform interpolation, so the image may not be smooth, but this does not affect the results.

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import make_interp_spline

plt.rcParams['font.family'] = 'WenQuanYi Zen Hei'

# Read and process the data
data = []
with open('problem1-1.txt', 'r') as file:
    for line in file:
        parts = line.strip().split()
        numbers = list(map(int, parts[:-1]))  # Take the first four numbers
        direction = parts[-1]  # The last letter indicates the direction

        # Perform a cyclic shift based on the direction
        if direction == 'S':
            numbers = numbers[1:] + [numbers[0]]  # Shift left by 1
        elif direction == 'W':
            numbers = numbers[2:] + numbers[:2]  # Shift left by 2
        elif direction == 'N':
            numbers = numbers[3:] + numbers[:3]  # Shift left by 3
        # If it's 'E', do nothing, keep as is

        data.append(numbers)  # Save the processed numbers

# Output the final numerical matrix
for row in data:
    print(row)

# Convert to a NumPy array for easier computation
matrix = np.array(data)

# Calculate the average of each column
column_means = matrix.mean(axis=0)

# Output the average of each column
print("Average of each column:")
for i, mean in enumerate(column_means, start=1):
    print(f"Average of column {i}: {mean:.2f}")

# Generate a line chart
num_rows = matrix.shape[0]
x = np.arange(num_rows)  # Create indices for the X-axis

# Plot each column's data as a line
plt.figure(figsize=(10, 6))
for i in range(matrix.shape[1]):
    plt.plot(x, matrix[:, i], label=f'Column {i+1}')

# Set graph labels and title
plt.xlabel('Row Number')
plt.ylabel('Value')
plt.title('Line Chart of Shanten Count by Column')
plt.legend()

# Display the graph
plt.show()

South Round, Second Place:

Average of each column:
Average of column 1: 4.17
Average of column 2: 4.00
Average of column 3: 3.75
Average of column 4: 3.50

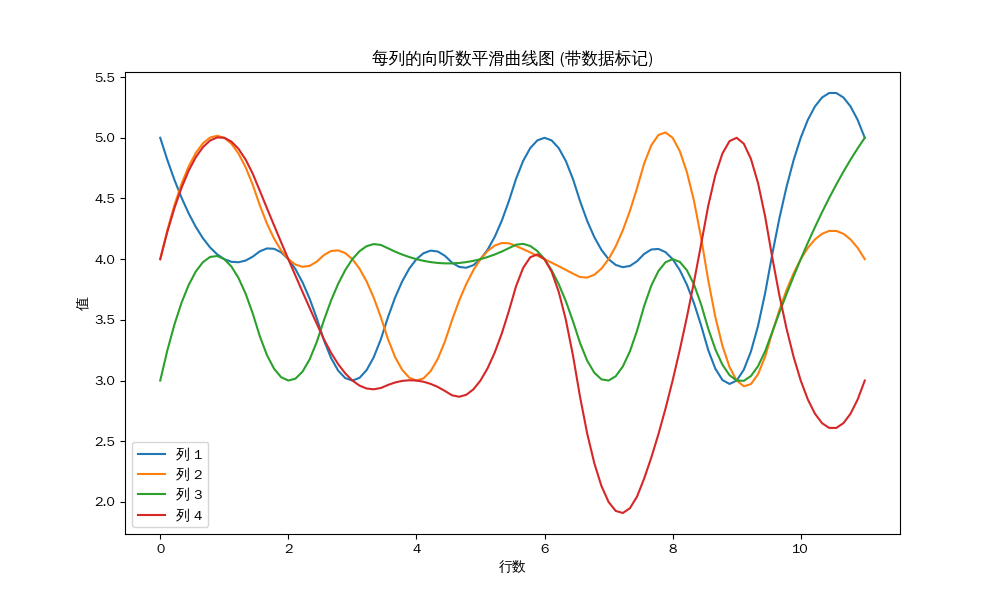
South Round, Fourth Place:

Average of each column:
Average of column 1: 3.88
Average of column 2: 3.81
Average of column 3: 3.31
Average of column 4: 3.44

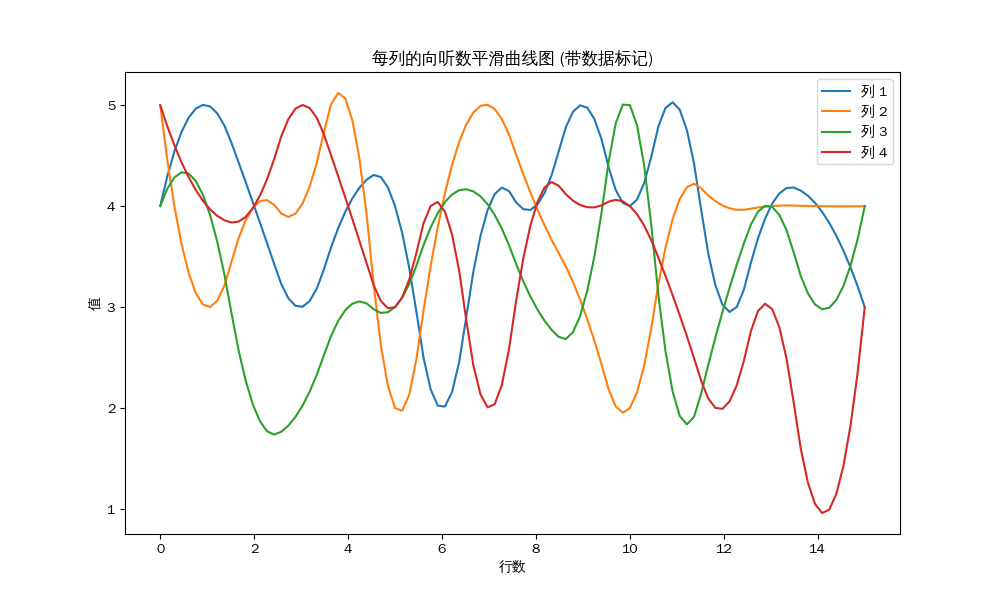
East Round, Second Place:

Average of each column:
Average of column 1: 3.17
Average of column 2: 4.00
Average of column 3: 3.50
Average of column 4: 3.83

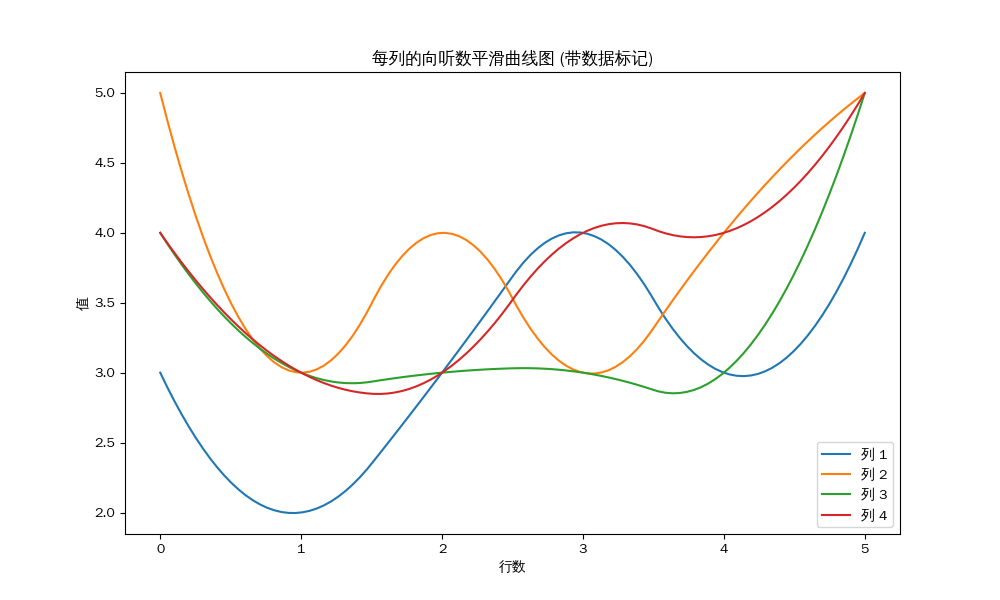
Conclusion: Although there is some variation in the shanten count among players, the difference is not significant enough to constitute a statistically meaningful gap. Therefore, it cannot be proven that there is unfairness during the initial tile distribution phase.

Experiment 2: Verifying Whether There is a Gap in the Shanten Count of Four Players Each Turn in Pure Tile Efficiency Play

My design idea is as follows: if Majsoul indeed places the tiles a player needs at the very end of the wall, then even if that player can "see the tiles for the next few turns" and make better decisions than a normal player, their shanten count would still be higher than that of other players.

Additionally, for the sake of coding convenience, assume that no calls (chi, pon, kan) occur during the game. This simplifies the code without affecting the results (since the tiles you want to draw are at the end, you still cannot draw them even with calls).

Therefore, we can design an algorithm based on Depth-First Search (DFS) to simulate the shanten count of a player each turn under the condition that they can foresee the next three draws and play with pure tile efficiency.

Below is the reference code:

#include <iostream>
#include <vector>
#include <assert.h>
#include <fstream>
#include <cmath>
#include "calsht.hpp"
#define CONFIG_SEARCH_DEPTH 3

Calsht calsht;
std::string tiles;
int curChange, bestChange;

// Function to convert a character to an index
int charToIndex(char ch) {
    if (ch >= '1' && ch <= '9') return ch - '1';
    if (ch == '0') return 4;
    std::cout << "Error: invalid character" << std::endl;
    exit(0);
}

int positionToIndex(char player_position) {
    if (player_position == 'E') return 0;
    if (player_position == 'S') return 1;
    if (player_position == 'W') return 2;
    if (player_position == 'N') return 3;
    std::cout << "Error: invalid position" << std::endl;
    exit(0);
}

// Deal four consecutive tiles to each player, three rounds, then deal one tile to East, South, West, North
int cal_offset(char player_position, int seq) {
    int offset = positionToIndex(player_position);

    if (seq < 12) {
        int round = seq / 4;
        return round * 16 + offset * 4 + seq % 4;
    } else if (seq == 12) {
        return 48 + offset;
    }
    assert(-1);
    return -1;
}

// The 53rd tile in the wall after dealing is the start of draws; the first 52 are used for dealing
int calcDrawIndex(char player_position, int turn) {
    int baseDraw = 52 + (turn - 1) * 4; // 4 tiles drawn per round
    int drawIndex = baseDraw + positionToIndex(player_position);
    
    return drawIndex;
}

int tilePositionTohandPosition(char number, char type) {
    int index = charToIndex(number);
    if (type == 'm') return index;
    if (type == 'p') return 9 + index;
    if (type == 's') return 18 + index;
    if (type == 'z') return 27 + index;
    assert(-1);
    return -1;
}

// Function to return the hand vector of a player based on the input wall string and player position
std::vector<int> parseHand(const std::string& tiles, char player_position) {
    std::vector<int> hand(34, 0);  // 34 elements, initialized to 0 (9 man + 9 pin + 9 sou + 7 honor tiles)
    
    for (int i = 0; i < 13; ++i) {
        char ch1 = tiles[cal_offset(player_position, i) * 2];   // First character is a number
        char ch2 = tiles[cal_offset(player_position, i) * 2 + 1]; // Second character is a letter m/p/s/z
        hand[tilePositionTohandPosition(ch1, ch2)]++;
    }

    return hand;
}

int getNewHandPosition(char player_position, int turn) {
    char ch1 = tiles[calcDrawIndex(player_position, turn) * 2];   // First character is a number
    char ch2 = tiles[calcDrawIndex(player_position, turn) * 2 + 1]; // Second character is a letter m/p/s/z
    int newHandPosition = tilePositionTohandPosition(ch1, ch2);
    return newHandPosition;
}

void dfsChangeHand(std::vector<int> curHand, int depth, int turn, 
        int& bestSht, std::vector<int>& bestHand, char player_position) {
    if (depth == 0) {
        return;  // Reached maximum depth, end search
    }

    auto [sht, mode] = calsht(curHand, 4, 7);

    if (sht <= bestSht) {
        bestSht = sht;
        bestHand = curHand;
        bestChange = curChange;
    }

    for (int i = 0; i < 34; i++) {
        if (curHand[i] > 0) {
            std::vector<int> newHand = curHand;
            newHand[i]--;  // Decrease current tile
            newHand[getNewHandPosition(player_position, turn)]++;  // Increase new tile

            auto [newSht, newMode] = calsht(newHand, 4, 7);
            
            // If the new hand is better than the current, continue deeper search
            if (newSht <= sht) {
                if (depth == CONFIG_SEARCH_DEPTH) {
                    curChange = i;
                }
                dfsChangeHand(newHand, depth - 1, turn + 1, bestSht, bestHand, player_position);
            }
        }
    }
}

// Modified changeHand function with recursive search
std::vector<int> changeHand(std::vector<int>& curHand, int turn, char player_position) {
    std::vector<int> bestHand = curHand;
    auto [bestSht, mode] = calsht(curHand, 4, 7);
    int curSht = bestSht;

    int searchDepth = CONFIG_SEARCH_DEPTH;  // Assume search depth is 3, adjust as needed
    dfsChangeHand(curHand, searchDepth, turn, bestSht, bestHand, player_position);

    if (bestSht < curSht) { 
        curHand[bestChange]--;
        curHand[getNewHandPosition(player_position, turn)]++;
    }
    return curHand;
}


int main(int argc, char* argv[])
{
    // Set the location of shanten tables
    calsht.initialize(".");


    std::ifstream file(argv[1]); // Open file
    std::string line;

    if (file.is_open()) {
        while (std::getline(file, line)) {  // Read line by line
            if (!line.empty()) {            // Check if it's an empty line
                // std::cout << line << std::endl;
                std::vector<char> player_position = {'E', 'S', 'W', 'N'};
                char direction = line[0];
                tiles = line.substr(2);

                for (auto p : player_position) {
                    std::vector<int> hand = parseHand(tiles, p);

                    auto [sht, mode] = calsht(hand, 4, 7);

                    std::cout << sht - 1 << " ";

                    for (int i = 1; i <= std::ceil((70 - positionToIndex(p)) / 4.0); i++) {
                        hand = changeHand(hand, i, p);  // Use the modified search algorithm
                        auto [sht, mode] = calsht(hand, 4, 7);
                        std::cout << sht - 1 << " ";
                    }
                    std::cout << p << " " << std::endl;

                }
                std::cout << direction << std::endl;
            }
            else {
                std::cout << std::endl;
            }
        }
        file.close();  // Close file
    } else {
        std::cerr << "Unable to open file" << std::endl;
        return 1;
    }
    return 0;
}

Substituting the previously obtained Majsoul input (here, I use my fourth-position South game as an example), we can get results similar to the following:

The first to fourth lines are the shanten counts of East, South, West, and North each turn, and the fifth line is the player's own position.

4 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 E 
5 4 4 3 3 2 2 2 2 2 2 2 2 2 1 1 1 1 1 S 
4 4 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 W 
5 4 3 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 N 
W
4 3 3 2 2 2 2 2 2 2 1 1 0 0 0 0 0 0 0 E 
4 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 1 1 S 
5 5 4 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 W 
3 3 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 N 
W
2 2 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 E 
4 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 S 
4 4 4 3 2 2 2 1 1 1 1 1 0 0 0 0 0 0 W 
4 3 3 3 3 2 1 0 0 0 0 0 0 0 0 0 0 0 N 
W
5 4 3 2 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 E 
3 3 3 2 2 2 2 2 1 1 0 0 0 0 0 0 0 0 0 S 
4 4 4 4 3 3 2 2 2 2 2 2 2 2 2 2 2 2 W 
2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 N 
S
4 3 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 E 
4 4 4 3 3 3 3 2 1 1 1 1 1 1 1 0 0 0 0 S 
5 5 4 3 3 3 3 2 1 1 1 0 0 0 0 0 0 0 W 
3 2 2 2 2 2 2 1 1 0 0 0 0 0 0 0 0 0 N 
S
3 2 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 E 
4 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 0 S 
2 2 2 2 2 2 2 1 1 1 1 0 0 0 0 0 0 0 W 
3 3 3 3 3 2 1 1 1 0 0 0 0 0 0 0 0 0 N 
S
4 4 4 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 E 
2 2 2 2 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 S 
4 4 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 W 
4 4 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 N 
S
2 2 2 2 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 E 
4 4 3 3 3 2 2 2 2 2 2 2 2 2 1 1 1 1 1 S 
5 4 3 3 3 3 2 2 2 1 1 1 0 0 0 0 0 0 W 
4 3 2 2 1 1 1 1 1 0 0 0 0 0 0 0 0 0 N 
S
4 4 4 4 3 2 2 2 2 2 2 2 1 1 1 1 1 1 1 E 
4 4 3 3 3 2 2 2 2 2 2 2 1 1 1 1 1 1 1 S 
3 3 2 2 2 1 1 1 1 0 0 0 0 0 0 0 0 0 W 
4 3 3 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 N 
E
3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 E 
3 2 2 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 S 
4 4 4 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 W 
5 5 5 4 4 4 3 3 2 2 1 1 1 1 1 1 1 1 N 
N
2 2 2 2 2 1 1 1 1 1 1 1 1 0 0 0 0 0 0 E 
5 4 3 3 3 3 2 2 2 2 2 2 2 1 1 0 0 0 0 S 
4 4 3 3 3 3 3 3 2 2 2 2 1 1 1 1 1 1 W 
4 4 4 3 3 2 2 2 2 2 2 1 1 0 0 0 0 0 N 
N
4 3 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 E 
2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 0 0 0 0 S 
3 3 3 2 2 2 2 2 1 1 1 0 0 0 0 0 0 0 W 
5 5 4 3 3 2 2 2 2 2 1 1 1 1 1 1 0 0 N 
N
3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 E 
2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 S 
3 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 W 
4 4 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 N 
W
3 3 2 2 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 E 
4 3 3 2 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 S 
4 3 3 3 3 3 3 2 2 2 2 2 1 1 1 1 1 0 W 
4 4 4 4 3 3 3 3 2 2 2 2 2 1 1 1 1 1 N 
S
4 4 4 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 E 
4 3 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 S 
3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 W 
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 N 
E
4 3 3 3 3 3 3 2 2 1 1 1 1 1 1 1 1 1 1 E 
4 4 3 3 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 S 
3 3 2 2 2 2 2 1 0 0 0 0 0 0 0 0 0 0 W 
3 3 2 2 2 2 2 2 1 1 0 0 0 0 0 0 0 0 N 
N

Then, using python's matplotlib library as usual, we can get a line chart like this:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import make_interp_spline

plt.rcParams['font.family'] = 'WenQuanYi Zen Hei'

tenpai_cnt = 0
tot_cnt = 0

# 模拟从文件中读取数据的函数
def read_data_from_file(file_path):
    with open(file_path, 'r') as file:
        data_block = []
        while True:
            lines = [file.readline().strip() for _ in range(5)]
            if lines[0] == '':  # 遇到空行结束
                break
            data_block.append(lines)
        return data_block

# 解析每个数据块并生成统计图
def plot_data_blocks(data_blocks):
    global tot_cnt, tenpai_cnt
    for block_index, block in enumerate(data_blocks):
        tot_cnt += 1
        data = []
        labels = []

        # 解析数据块中的每行数据
        for line in block[:-1]:  # 最后一行是方位字母，不包含数值
            values = list(map(int, line.split()[:-1]))  # 去掉方位字母，保留数值
            labels.append(line.split()[-1])  # 保存方位字母
            data.append(values)

        highlight_label = block[-1].strip()  # 最后一行表示需要highlight的方位

        # 绘制每个数据块的统计图
        plt.figure(figsize=(10, 6))
        for i, row in enumerate(data):
            x = np.arange(len(row))
            x_smooth = np.linspace(x.min(), x.max(), 300)
            spl = make_interp_spline(x, row, k=2)
            y_smooth = spl(x_smooth)
    
            # 如果是需要highlight的方位，使用红色，否则使用灰色
            if labels[i] == highlight_label:
                if 0 in row:
                    tenpai_cnt += 1
                plt.plot(x_smooth, y_smooth, label=labels[i], color='red', linewidth=2)
            else:
                plt.plot(x_smooth, y_smooth, label=labels[i], color='gray', alpha=0.6)

        plt.title(f'统计图 - 第 {block_index + 1} 个数据块')
        plt.xlabel('Index')
        plt.ylabel('Value')
        plt.legend()
        plt.grid(True)
        plt.show()

# 测试代码（使用从文件读取的数据）
file_path = '../build/problem3.txt' 
blocks = read_data_from_file(file_path)
plot_data_blocks(blocks)

We can get the following results:

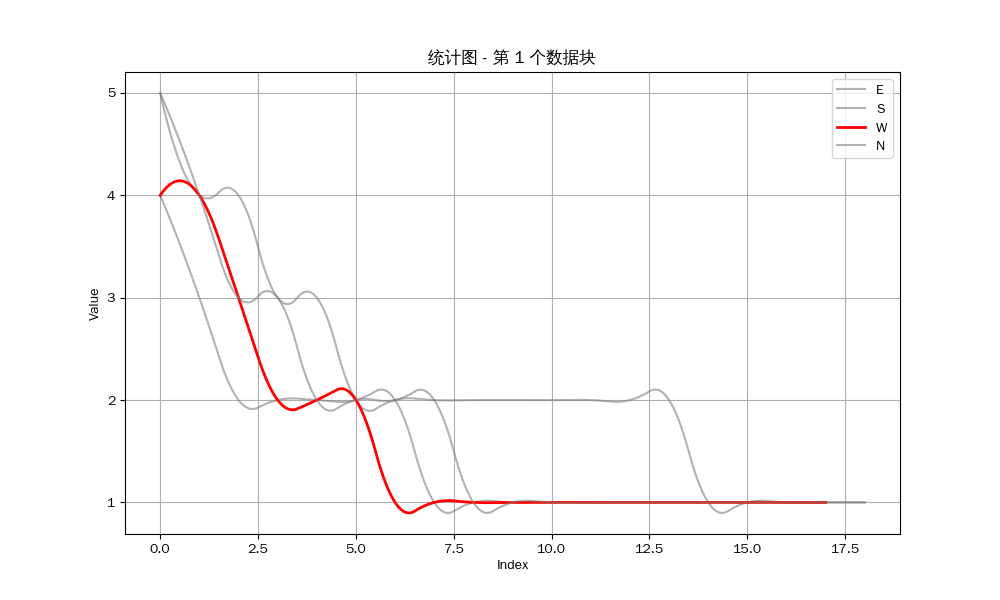
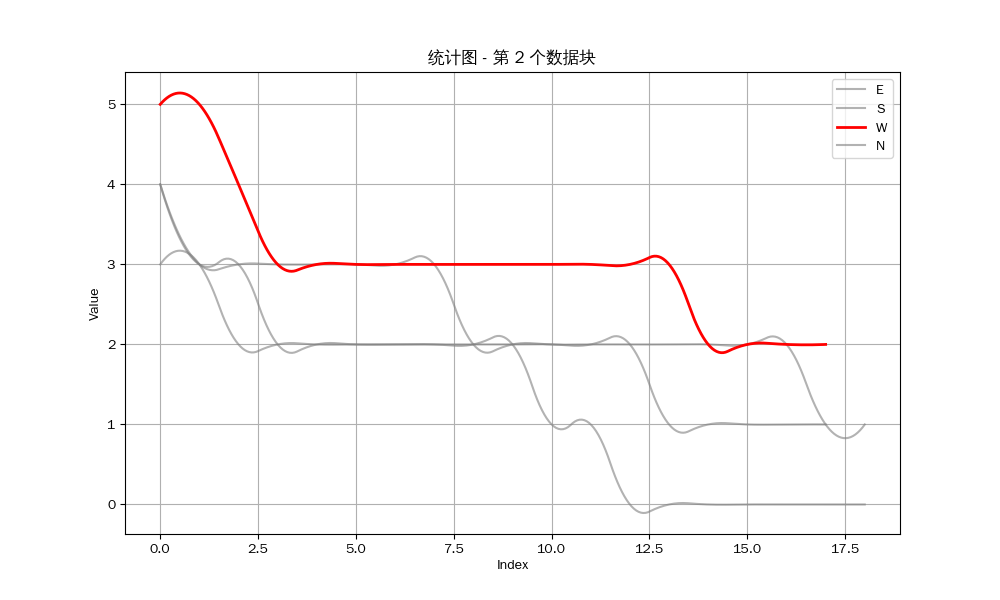
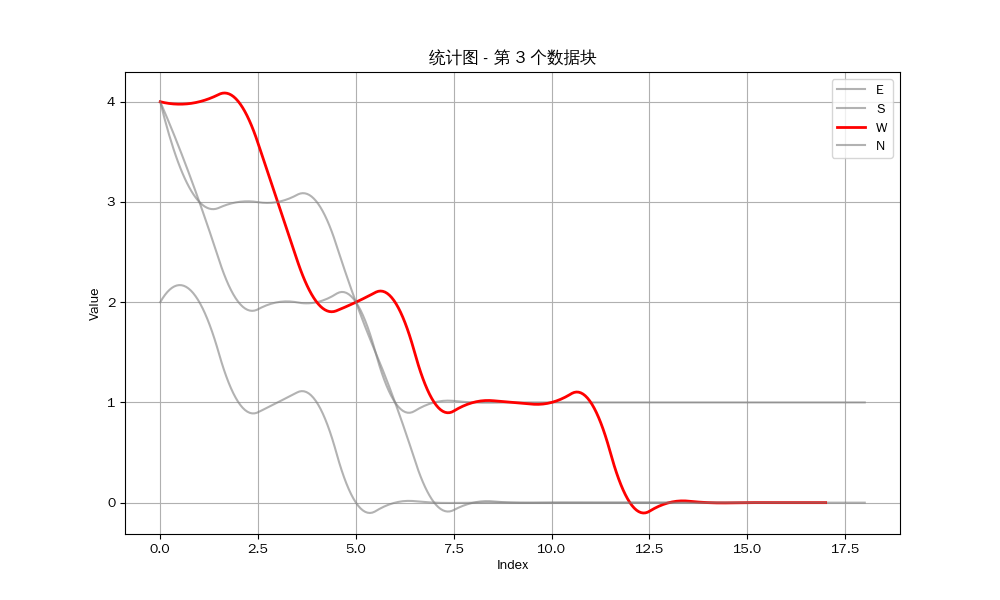
As we all know, Riichi Mahjong emphasizes defense. If you sense that your opponent is drawing a hand, and if you are not completely confident in your hand, you should choose to forfeit the draw to prevent losses. Therefore, whether you can frequently draw the first hand is the key to winning the game.

However, the statistical chart shows that we either couldn't draw or couldn't be the first player to draw. I visually inspected the remaining 12 data sets and found only one in which I, as North, drew on the same round as East. But because I was North, I couldn't be the first player to draw. In other words, at least in this data set, I didn't draw first once.

So how do we calculate whether this data is reasonable? We can first calculate the probability of each player being the first to draw a hand under absolutely fair conditions. We can make the following rough estimate:

According to statistics⁵, we know that the probability of a winning hand in a Mahjong game is 84%, and waiting for a hand is a necessary condition for a winning hand, so the probability of each player being the first to wait for a hand is about 21%.

Next, we can calculate the probability of my situation happening:

P = (1 - 0.21)^{16} = 0.023 < 0.05

This is clearly a very small probability, so we can consider this scenario unreasonable.

Conclusion: Mahjong Souls does have the potential to influence a player's winning streak by manipulating the deck (for example, placing the desired card at the end of the deck). Mahjong Souls's dealings are likely to be unfair in the short term.

Experiment 3: Calculating the Average Tenpai Probability for Each Player

The original Python code can be slightly modified as follows:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interp1ate import make_interp_spline

plt.rcParams['font.family'] = 'WenQuanYi Zen Hei'

tenpai_cnt = 0
tot_cnt = 0

# Function to simulate reading data from a file
def read_data_from_file(file_path):
    with open(file_path, 'r') as file:
        data_block = []
        while True:
            lines = [file.readline().strip() for _ in range(5)]
            if lines[0] == '':  # End when encountering an empty line
                break
            data_block.append(lines)
        return data_block

# Parse each data block and generate statistical plots
def plot_data_blocks(data_blocks):
    global tot_cnt, tenpai_cnt
    for block_index, block in enumerate(data_blocks):
        tot_cnt += 1
        data = []
        labels = []

        # Parse each line of data in the block
        for line in block[:-1]:  # The last line contains direction letters, not numerical values
            values = list(map(int, line.split()[:-1]))  # Remove direction letters, keep numerical values
            labels.append(line.split()[-1])  # Save direction letters
            data.append(values)

        highlight_label = block[-1].strip()  # The last line indicates the direction to highlight

        # Plot the statistical graph for each data block
        plt.figure(figsize=(10, 6))
        for i, row in enumerate(data):
            x = np.arange(len(row))
            x_smooth = np.linspace(x.min(), x.max(), 300)
            spl = make_interp_spline(x, row, k=2)
            y_smooth = spl(x_smooth)
    
            # Use red for the direction to highlight, gray for others
            if labels[i] == highlight_label:
                if 0 in row:
                    tenpai_cnt += 1
                plt.plot(x_smooth, y_smooth, label=labels[i], color='red', linewidth=2)
            else:
                plt.plot(x_smooth, y_smooth, label=labels[i], color='gray', alpha=0.6)

        plt.title(f'Statistical Graph - Data Block {block_index + 1}')
        plt.xlabel('Index')
        plt.ylabel('Value')
        plt.legend()
        plt.grid(True)
        # plt.show()

# Test code (using data read from the file)
file_path = '../build/problem3.txt'
blocks = read_data_from_file(file_path)
plot_data_blocks(blocks)
print(tot_cnt, tenpai_cnt)
print(tenpai_cnt / tot_cnt)

In the 34-game sample from Mahjong Soul, I successfully achieved tenpai 17 times, resulting in an average tenpai probability of 0.5.

The average tenpai probabilities for the other three players are 0.441, 0.588, and 0.588, respectively.

Conclusion: Although there are differences in the average tenpai probabilities, the differences are not significant. I believe they do not constitute a statistically significant disparity, and therefore, it cannot be concluded that there is unfairness in the tenpai probability.

Experiment 4: Comparing These Data with Tenhou

Initial Deal

I believe that since Tenhou has publicly disclosed the tile wall generation code, and reference materials² have also verified it, and because Tenhou's tile wall code is based on the mt19937 pseudorandom number generator, we can consider Tenhou's tile wall to be random.

For the average starting shanten count from 25 sets of Tenhou data, the results are as follows:

Average value per column:
Average of Column 1: 3.52
Average of Column 2: 3.60
Average of Column 3: 3.44
Average of Column 4: 3.72

And here are the results from 34 sets of Mahjong Soul data:

Average value per column:
Average of Column 1: 3.85
Average of Column 2: 3.91
Average of Column 3: 3.50
Average of Column 4: 3.53

Intuitively, the average starting shanten count for the four players in Mahjong Soul is higher than in Tenhou, and the range is larger (even with a larger sample size for Mahjong Soul). Therefore, we can consider that Mahjong Soul's hand generation may not be random.

During the Game

The previous section has demonstrated that the dealing in Mahjong Soul is likely unfair in the short term. Since randomness is a necessary condition for fairness, we can conclude that the tile wall during the game in Mahjong Soul is not random.

Tenpai Probability

We applied the same code for calculating tenpai probability to Tenhou data, and the results showed that in 25 matches on Tenhou, I was able to achieve tenpai 19 times. As mentioned earlier, in 34 matches on Mahjong Soul, I only achieved tenpai 17 times.

In the Probability and Mathematical Statistics course during the first semester of my sophomore year, we learned about hypothesis testing. Here, we can use a one-tailed two-sample proportion test to determine whether the tenpai rate on Mahjong Soul is significantly lower than that on Tenhou:

To determine whether the success rate of A (Mahjong Soul) is significantly lower than that of B (Tenhou), we can perform a one-tailed two-sample proportion test, rather than a two-tailed test. This test is used to determine whether the success rate of A is significantly lower than that of B.

Sample A: 17 successes, sample size 34, success rate $p_{A} = \frac{17}{34} = 0.5$
Sample B: 19 successes, sample size 25, success rate $p_{B} = \frac{19}{25} = 0.76$

Set Hypotheses:
- Null Hypothesis ( $H_{0}$ ): The success rates of A and B are equal, i.e., $p_{A} = p_{B}$ .
- Alternative Hypothesis ( $H_{1}$ ): The success rate of A is less than that of B, i.e., $p_{A} < p_{B}$ .
Calculate the Overall Success Rate (pooled success rate $p_{pool}$ ):
$p_{pool} = \frac{Successes in A + Successes in B}{Sample size of A + Sample size of B} = \frac{17 + 19}{34 + 25} = \frac{36}{59} \approx 0.6102$
Calculate the Standard Error:
$S E = \sqrt{p_{pool} \cdot (1 - p_{pool}) \cdot (\frac{1}{n_{A}} + \frac{1}{n_{B}})}$
where $n_{A} = 34$ , $n_{B} = 25$ . Substituting the values:
$S E = \sqrt{0.6102 \cdot (1 - 0.6102) \cdot (\frac{1}{34} + \frac{1}{25})} \approx 0.1289$
Calculate the z-value:
$z = \frac{p_{A} - p_{B}}{S E} = \frac{0.5 - 0.76}{0.1289} \approx - 2.016$
Find the p-value (one-tailed test): According to the standard normal distribution table, the one-tailed p-value corresponding to a z-value of -2.016 is approximately 0.022.
Conclusion:
- If the p-value is less than the significance level (typically α = 0.05), we reject the null hypothesis and conclude that the success rate of A is significantly lower than that of B.
- Here, the p-value is 0.022, which is clearly less than 0.05. Therefore, we reject the null hypothesis, and the success rate of A is significantly lower than that of B.

At a significance level of 0.05, there is a significant difference between the success rate of A (50%) and that of B (76%), with the success rate of A being significantly lower. Therefore, from the perspective of tenpai probability, Mahjong Soul's tile distribution is definitely not random.

Experimental Summary

The average starting shanten number in Mahjong Soul is higher, and the variance is also greater. This aligns with the perception that "Mahjong Soul's initial hands are more extreme."
Mahjong Soul likely reduces a player's win rate by placing the tiles they need at the end of the wall. Therefore, Mahjong Soul lacks fairness on a short time scale.
Mahjong Soul's tile distribution lacks randomness. It can be argued that every player in Mahjong Soul experiences unfavorable conditions, albeit to varying degrees.