Is multimod_fast really correct?

This story starts with this piece of code:

// gcc test.c -o test -fwrapv
int64_t multimod_fast(int64_t a, int64_t b, int64_t m) {
    int64_t t = (a * b - (int64_t)((double)a * b / m) * m) % m;
    return t < 0 ? t + m : t;
}

Last night, someone sent me this code, claiming it could serve as a replacement for fast multiplication, and asked me to explain its correctness. This code supposedly reduces the time complexity from $O (\log (n))$ to $O (1)$ . Obviously, we all know that casting between int64_t and double can lead to loss of precision, so I became skeptical about the correctness of this code.

Preliminaries

First, we need to understand how floating-point numbers are represented in C. The IEEE 754 standard specifies the representation of floating-point numbers. The double type occupies 64 bits, with 1 bit for the sign, 11 bits for the exponent, and the remaining 52 bits for the mantissa. You can refer to this article to learn more about floating-point numbers; I won't go into further detail here.

Next, we need to understand the role of the -fwrapv compilation option. According to the official GCC documentation, the -fwrapv option ensures that when signed integer overflow occurs, the result is the two's complement modulo. This means that when signed integers overflow, the result is truncated to a valid value. For example, INT_MAX + 1 results in INT_MIN.

Error Analysis

(double)a

Based on the knowledge learned earlier, it can be inferred that the relative precision of a 64-bit floating-point number is $2^{- 52 - 1}$ (why?). Then, theoretically, what would be the absolute precision when casting int64_t to double? We can use simple mathematical derivation to find the answer.

We know that the range of int64_t is $[- 2^{63}, 2^{63} - 1]$ . Therefore, the maximum absolute precision can be roughly estimated as $2^{63} \times 2^{- 53} = 2^{10}$ . This means that when casting int64_t to double, the maximum absolute error is approximately $2^{10}$ .

Next, we can try to construct a test case to verify this conclusion:

#include <stdio.h>
#include <stdint.h>
#include <math.h>

int64_t a = 9223372036854775807;
double b;


int equal(double x, double y) {
  return fabs(x - y) < 0.0000001;
}

int judge(int64_t offset) {
  double c = (double)(a - offset);
  return equal(c, b);
}

int64_t bisect(int64_t low, int64_t high) {
  if (low == high) {
    return low - 1;
  }
  int64_t mid = (low + high) / 2;
  if (judge(mid)) {
    return bisect(mid + 1, high);
  } else {
    return bisect(low, mid);
  }
}

int main() {
  b = (double)a;
  printf("%ld\n", bisect(1, 1000000000));
  double c = (double)(a - 512);
  printf("%lf %lf\n", b, c);
  //printf("%d\n", equal(b, c));
  //printf("%d\n", judge(200000000));
  return 0;
}

Actual testing shows that when a = INT64_MIN, the valid range for the bisection offset is $[0, 512]$ ; when a = INT64_MAX, the valid range for the bisection offset is $[- 511, 0]$ . Combined, the valid range for a is $[- 511, 512]$ . If it exceeds this valid range, the converted double value jumps from $\pm 9223372036854775808$ to $\pm 9223372036854774784$ , which differs by exactly $1024$ , or $2^{10}$ .

(double)a * b

asm

Let's analyze how a double is multiplied by an int64_t with a simple code snippet:

int main() {
  int64_t a = 3;
  int64_t b = 4;
  double c = (double)a * b;
  return 0;
}

The disassembly in an x86_64 environment is as follows:

0000000000001119 <main>:
    1119:       55                      push   rbp
    111a:       48 89 e5                mov    rbp,rsp
    111d:       48 c7 45 e8 03 00 00    mov    QWORD PTR [rbp-0x18],0x3
    1124:       00 
    1125:       48 c7 45 f0 04 00 00    mov    QWORD PTR [rbp-0x10],0x4
    112c:       00 
    112d:       66 0f ef c9             pxor   xmm1,xmm1
    1131:       f2 48 0f 2a 4d e8       cvtsi2sd xmm1,QWORD PTR [rbp-0x18]
    1137:       66 0f ef c0             pxor   xmm0,xmm0
    113b:       f2 48 0f 2a 45 f0       cvtsi2sd xmm0,QWORD PTR [rbp-0x10]
    1141:       f2 0f 59 c1             mulsd  xmm0,xmm1
    1145:       f2 0f 11 45 f8          movsd  QWORD PTR [rbp-0x8],xmm0
    114a:       b8 00 00 00 00          mov    eax,0x0
    114f:       5d                      pop    rbp
    1150:       c3                      ret

Clearly, not everyone is familiar with the meanings of the pxor, cvtsi2sd, mulsd, and movsd instructions. Let's refer to the Intel manual:

pxor: Performs a bitwise XOR operation on floating-point registers (xmm?).
cvtsi2sd: Converts an int64_t to a double and stores it in a floating-point register.
mulsd: Multiplies two double values and stores the result in the first (destination) operand.
movsd: Copies the source operand to the destination operand.

In GDB, set a breakpoint at 0x114a with b 0x114a, then continue. After the breakpoint is hit, the state of xmm0 is as follows:

(gdb) p $xmm0
$4 = {v8_bfloat16 = {0, 0, 0, 2.625, 0, 0, 0, 0}, v8_half = {0, 0, 0, 2.0781, 0, 0, 
    0, 0}, v4_float = {0, 2.625, 0, 0}, v2_double = {12, 0}, v16_int8 = {0, 0, 0, 0, 
    0, 0, 40, 64, 0, 0, 0, 0, 0, 0, 0, 0}, v8_int16 = {0, 0, 0, 16424, 0, 0, 0, 0}, 
  v4_int32 = {0, 1076363264, 0, 0}, v2_int64 = {4622945017495814144, 0}, 
  uint128 = 4622945017495814144}

Looking up the relevant data online, we find that converting the double value 4622945017495814144 back to int64_t gives the correct result: 12.

Actual Analysis

From the above, it can be inferred that the computation of (double)a * b involves converting both a and b to floating-point form and then executing the mulsd instruction.

Next, let's analyze the result of (double)a * b. We already know that when converting int64_t to double, the error range for the multiplier is $[- 511, 512]$ . Since the principles of IEEE 754 floating-point multiplication are relatively complex, I plan to directly estimate using the previously accumulated arithmetic error range: $[(2^{63} - 1) (- 2^{63}) - (2^{63} - 512) (- 2^{63} + 512), (2^{63})^{2} - (2^{63} - 512)^{2}]$ .

For the maximum value:

(2^{63})^{2} - (2^{63} - 512)^{2} = 2 \times 2^{63} \times 2^{9} - 512^{2} = 2^{73} - 2^{18}

For the minimum value:

(2^{63} - 512)^{2} - (2^{63})^{2} + 2^{63} = ((2^{63})^{2} - 2 \times 2^{63} \times 512 + 512^{2}) - (2^{63})^{2} + 2^{63} = - 2^{73} + 2^{18} + 2^{63}

Let's write another piece of code to verify whether this conjecture is correct:

#include <stdio.h>
#include <stdint.h>
#include <math.h>

int64_t a = -9223372036854775808;
double b;


int equal(double x, double y) {
  printf("fabs(%lf - %lf) = %lf\n", x, y, fabs(x - y));
  return fabs(x - y) < 0.0000001;
}

int judge(int64_t offset) {
  double c = (double)(a + offset)*(a + offset);
  // should be (double)(a + offset)*(-a + offset) when getting the minimum
  return equal(c, b);
}

int64_t bisect(int64_t low, int64_t high) {
  if (low == high) {
    return low - 1;
  }
  int64_t mid = (low + high) / 2;
  if (judge(mid)) {
    return bisect(mid + 1, high);
  } else {
    return bisect(low, mid);
  }
}

int main() {
  // the "b" in context is another a in next line of code, 
  // instead of the result on the left
  // should be (double)a*(-a) when getting the minimum
  b = (double)a*a;
  printf("%ld\n", bisect(1, 1000000000));
  //double c = (double)(a - 512);
  //printf("%lf %lf\n", b, c);
  //printf("%d\n", equal(b, c));
  //printf("%d\n", judge(200000000));
  return 0;
}

The verification results show that the valid range of values for a and b remains unchanged. When a = b = INT64_MIN and offset = 512, the maximum absolute error is calculated to be $18889465931478580854784$ , which is $2^{74}$ . Similarly, when a = INT64_MAX, b = -INT64_MAX and offset = -511, the minimum absolute error is calculated to be $- 2^{74}$ .

In summary, our previous estimate is about half the actual absolute error, which is still acceptable.

(double)a * b / m

Division is somewhat tricky. According to the relative error formula, if $c = \frac{a}{b}$ , then:

\frac{Δ c}{c} = \frac{Δ a}{a} + \frac{Δ b}{b}

There is a relatively simple positive correlation between $Δ c$ and $Δ a$ , so to find the extreme value, we set $a = 2^{63} - 1$ , and thus $\frac{Δ a}{a} = 2^{- 53}$ .

For $b$ , due to the nature of floating-point operations, $\frac{Δ b}{b}$ remains $0$ when $b < 2^{53}$ , and jumps to $2^{- 53}$ in the interval $[2^{53}, 2^{63} - 1]$ . Let's slightly rearrange the expression:

Δ c = \frac{Δ a}{a} c + \frac{Δ b}{b} c = \frac{Δ a}{b} + \frac{a Δ b}{b^{2}}

\begin{array}{r} = {\begin{cases} 2^{- 53} \frac{a}{b} & if b < 2^{53} \\ 2^{- 52} \frac{a}{b} & if b \in [2^{53}, 2^{63} - 1] \end{cases} \end{array}

We can observe that $Δ c$ is generally a decreasing function and is non-monotonic only at $b = 2^{53}$ . Clearly, the extreme value of $Δ c$ does not occur at $b = 2^{53}$ , so we can conclude that the maximum absolute error of the quotient still occurs when $b = 1$ .

Substituting back into the original expression (double)a * b / m, we can confirm that when a = b = INT64_MIN, m = 1 and a = b = INT64_MIN, m = -1, the absolute error range is $[- 2^{74}, 2^{74}]$ .

(int64_t)((double)a * b / m) * m

The absolute error of (double)a * b / m has already exceeded the range of int64_t itself, so theoretically, after converting to int64_t, there is no precision at all in the worst-case scenario.

Therefore, from a mathematical perspective, this function is not always valid. There is no further need to analyze it.

When it will satisfy

Let's then examine at what magnitudes of $a$ , $b$ , and $m$ the expression (int64_t)((double)a * b / m) * m will be divisible by $m$ .

import random
import subprocess

matrix = [[1 for _ in range(62)] for _ in range(62)]


# try this multiple times to reduce the chance of false positive   
for _ in range (10):

    A = []
    B = []
    C = []

    for i in range(0, 62):
        A.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    for i in range(0, 62):
        B.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    for i in range(0, 62):
        C.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    lenA = len(A)
    lenC = len(C)


    for i in range(lenA):
        for j in range(lenC):
            command = ["./test", str(A[i]), str(B[i]), str(C[j])]
            result = subprocess.run(command, stdout=subprocess.PIPE)
            output = int(result.stdout.strip())
            if output % C[j] != 0:
                matrix[i][j] = 0 # invalid

import numpy as np
import matplotlib.pyplot as plt

colored_matrix = np.array(matrix)
plt.imshow(colored_matrix, cmap='Blues', interpolation='nearest')
plt.show()

#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
#include <math.h>


double f(int64_t x, int64_t y, int64_t z) {
  return (int64_t)((double)x * y / z) * z;
}

double g(int64_t x, int64_t y, int64_t z) {
  return (double)x * y / z;
}

int64_t h(int64_t x, int64_t y, int64_t z) {
  return (int64_t)((double)x * y / z) * z;
}

int64_t multimod_fast(int64_t a, int64_t b, int64_t m) {
    int64_t t = (a * b - (int64_t)((double)a * b / m) * m) % m;
    return t < 0 ? t + m : t;
}


int main(int argc, char *argv[]) {
  if (argc != 4) {
    return 1;
  }

  int64_t a = atol(argv[1]);
  int64_t b = atol(argv[2]);
  int64_t c = atol(argv[3]);

  printf("%ld\n", h(a, b, c));
  return 0;
}

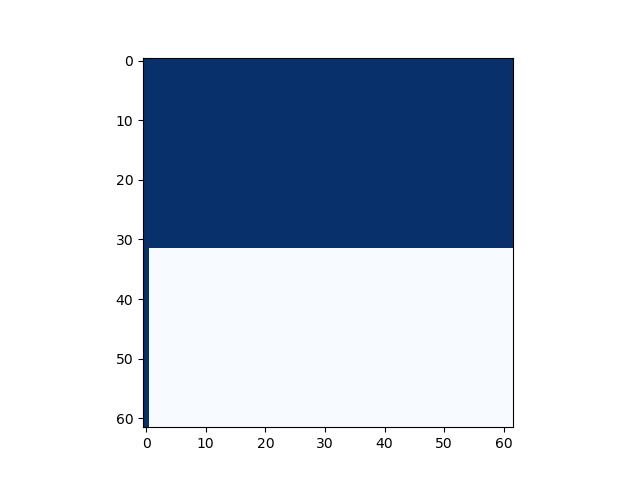
The plotting result is as follows (the horizontal axis is $\log_{2} m$ , the vertical axis is $\log_{2} a$ and $\log_{2} b$ , blue indicates correct results). It can be observed that the result is correct only when $a, b < 2^{31}$ or $m = 1$ .

Let's slightly modify the code. Theoretically, if (int64_t)((double)a * b / m) * m is a multiple of $m$ , then (a * b - (int64_t)((double)a * b / m) * m) % m should simplify to (a * b) % m. That is, the entire multimod_fast is equivalent to the previous proposition, and the plotted graph should be consistent:

import random
import subprocess

matrix = [[1 for _ in range(62)] for _ in range(62)]


# try this multiple times to reduce the chance of false positive   
for _ in range (10):

    A = []
    B = []
    C = []

    for i in range(0, 62):
        A.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    for i in range(0, 62):
        B.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    for i in range(0, 62):
        C.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    lenA = len(A)
    lenC = len(C)


    for i in range(lenA):
        for j in range(lenC):
            command = ["./test", str(A[i]), str(B[i]), str(C[j])]
            result = subprocess.run(command, stdout=subprocess.PIPE)
            output = int(result.stdout.strip())
            if output != A[i] * B[i] % C[j]:
                matrix[i][j] = 0 # invalid

import numpy as np
import matplotlib.pyplot as plt

colored_matrix = np.array(matrix)
plt.imshow(colored_matrix, cmap='Blues', interpolation='nearest')
plt.show()

#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
#include <math.h>


double f(int64_t x, int64_t y, int64_t z) {
  return (int64_t)((double)x * y / z) * z;
}

double g(int64_t x, int64_t y, int64_t z) {
  return (double)x * y / z;
}

int64_t h(int64_t x, int64_t y, int64_t z) {
  return (int64_t)((double)x * y / z) * z;
}

int64_t multimod_fast(int64_t a, int64_t b, int64_t m) {
    int64_t t = (a * b - (int64_t)((double)a * b / m) * m) % m;
    return t < 0 ? t + m : t;
}


int main(int argc, char *argv[]) {
  if (argc != 4) {
    return 1;
  }

  int64_t a = atol(argv[1]);
  int64_t b = atol(argv[2]);
  int64_t c = atol(argv[3]);

  printf("%ld\n", multimod_fast(a, b, c));
  return 0;
}

However, the actual graph looks like this. We found that the previous expression is a sufficient condition and is not equivalent. Also, when $m \geq 2^{31}$ , the larger $m$ is, the more $a$ and $b$ values satisfy the condition, which aligns with our intuition.

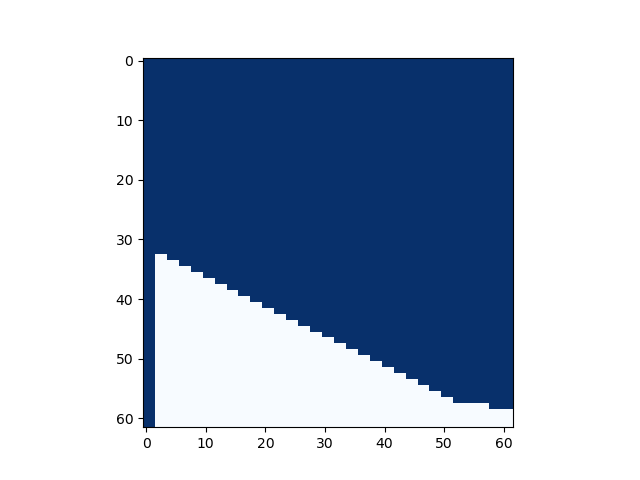
We can also provide a concrete counterexample: $a = 2^{61} + 1, b = 2^{46} + 3, m = 23$ . The result of multimod_fast is $12$ , but the correct result is $18$ , which roughly falls into the white area in the graph.

Overall, we can at least conclude that when $a, b < 2^{31}$ , this expression always holds. Next, let's attempt to prove it.

Proof

We previously stated that "(int64_t)((double)a * b / m) * m being a multiple of $m$ " is a sufficient condition for the function to return the correct result. Therefore, we only need to prove that when $a, b < 2^{31}$ , the expression (int64_t)((double)a * b / m) * m is a multiple of $m$ .

Some might question: isn't (int64_t)((double)a * b / m) definitely an integer? Then the expression in question must be a multiple of $m$ . These individuals overlook one issue: 64-bit integer signed overflow. Even if we enable the -fwrapv option, if $m ∤ 2^{64}$ , then after overflow, the expression in question will still not be a multiple of $m$ .

Therefore, as long as $a \times b$ itself does not overflow, then (int64_t)((double)a * b / m) * m must be a multiple of $m$ . And $a, b < 2^{31}$ is a sufficient condition for the above (a stricter conclusion is $a \times b < 2^{63}$ ). In this case, multimod_fast correctly performs its function, regardless of floating-point errors.

Summary

The expression multimod_fast is correct only when $a \times b$ itself does not overflow int64_t. It cannot fully replace the $O (\log n)$ fast multiplication for int64_t values of $a$ and $b$ .