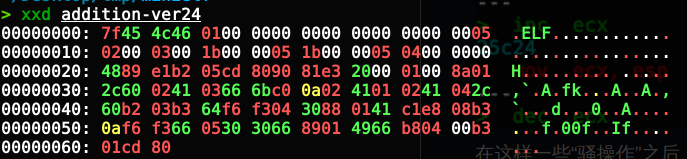
MiniELF

After several days of effort, I successfully compressed the program to 99 bytes.

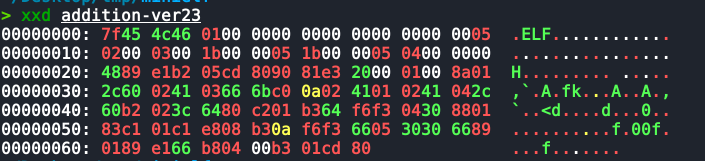
> xxd addition-ver24
00000000: 7f45 4c46 0100 0000 0000 0000 0000 0005  .ELF............
00000010: 0200 0300 1b00 0005 1b00 0005 0400 0000  ................
00000020: 4889 e1b2 05cd 8090 81e3 2000 0100 8a01  H......... .....
00000030: 2c60 0241 0366 6bc0 0a02 4101 0241 042c  ,`.A.fk...A..A.,
00000040: 60b2 03b3 64f6 f304 3088 0141 c1e8 08b3  `...d...0..A....
00000050: 0af6 f366 0530 3066 8901 4966 b804 00b3  ...f.00f..If....
00000060: 01cd 80                                  ...

MiniELF

A + B Problem

Read two integers from STDIN and output their sum to STDOUT.

The input consists of two two-digit integers separated by a space.

Ensure the output does not contain any extra carriage return (CR), line feed (LF), or CRLF characters.

Context

• Linux v5.8+ kernel
• glibc v2.33+
• Support dynamic linking
• x86_64 architecture

Score Calculation

You are guaranteed a score as long as the metrics you achieve are higher than a certain BASELINE (4096 bytes). Otherwise, your score is strictly determined by the following formula: (where $r$ represents your ranking, $s$ represents your final score, and $s_o$ represents the task's overall score)

$$s=\frac{2}{2^r}{s}_o$$

solution

Level 0 (Compile and Run in C)

A straightforward approach is to write an A+B problem in C, then compile and run it using gcc. Typically, the resulting executable size ranges from 15 to 17 KB. If you strip the symbol table, it can be reduced to around 14 KB.

In fact, there is an optimization strategy based on the C code: packing (or "packing" the executable). In some cases, packing not only obfuscates the code but also compresses the program size. For example, using UPX to pack the stripped executable can reduce its size to about 5 KB.

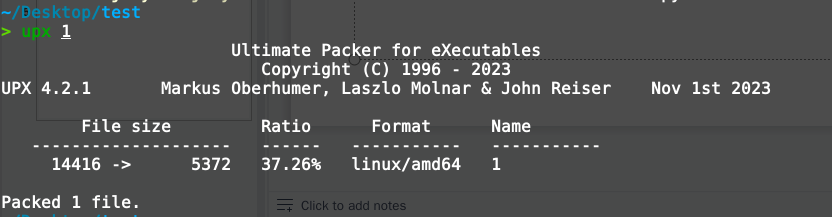
Level 1 (Write Assembly Directly)

Of course, since C language links to the relevant libraries of glibc during compilation (even with dynamic linking, the symbol table, PLT, GOT, etc., occupy a certain amount of space), and the scanf and printf we use can be replaced with syscall read/write, which should be common knowledge for those working with binaries.

Therefore, it's better to write assembly directly to eliminate the space consumption brought by glibc. I had GPT4 generate the corresponding assembly code, made some minor modifications, and it passed the challenge. The size was between 4–5 KB, but it still fell slightly short of the baseline.

Level 2 (Modifying the Start Address)

Then you'll notice that even when using assembly, the generated program still has a lot of unused space. For example, in the image below, there are a bunch of zero bytes starting from 0x150.

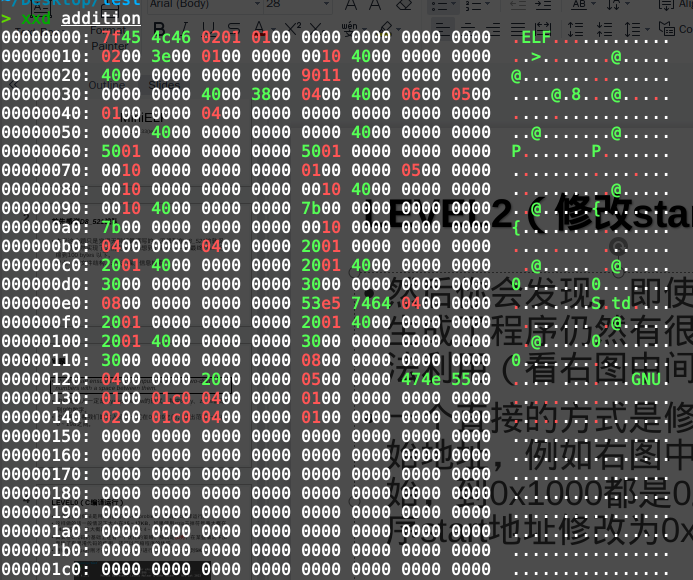
A straightforward approach is to modify the program's start address. For instance, in the right image, from 0x150 to 0x1000 are all zeros. You can change the program's start address to 0x400150. For specific modification methods, you can refer to man elf. Of course, you could also just blindly change all occurrences of 0x401000—it seems to work fine (one of them is at 0x18).

My final size was 652 bytes, which is enough to meet the baseline.

Level 3 (Trimming the ELF Header and Footer)

At this point, I came across this answer on Stack Overflow and realized that there was still room to trim the ELF header, and the footer could be completely removed.

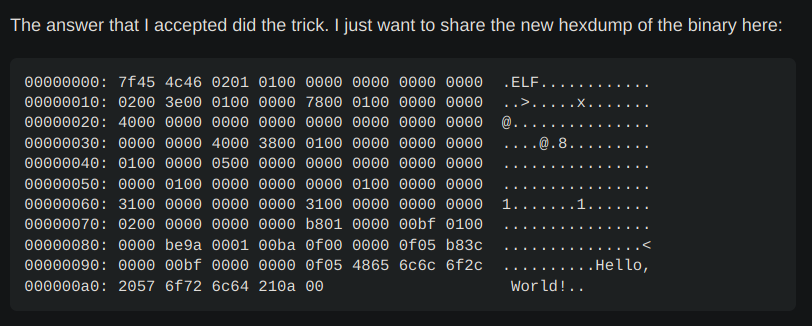
So, I copied the header from the answer, changed the start address from 0x78 to 0x74, and then overwrote the location at 0x74 with my own machine code. I ran it, and it actually worked!

As a result, my program size was reduced to 273 bytes.

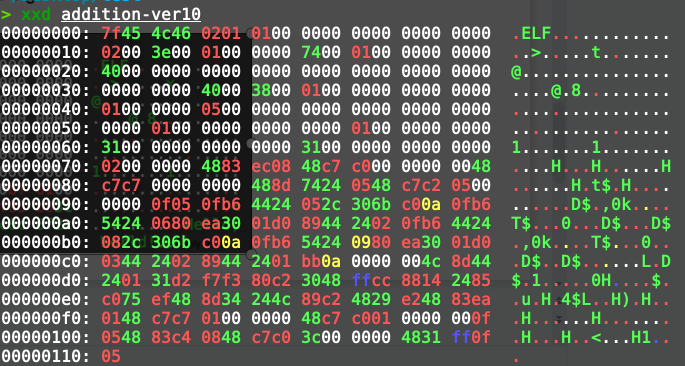
Level 4 (Further Trimming the Header)

After that, I did some more detailed trimming work, reducing the size from 273 bytes to 235 bytes. At that point, someone submitted a solution of 205 bytes—there was no way around it, the ELF header still needed further optimization.

I then found this answer, which compressed a "Hello, World!" program to an astonishing 61 bytes!

I studied it carefully for a while before understanding which parameters are indispensable when the ELF file is read. The specific explanations are as follows:

• The magic number 0x464c457f at the beginning of the file is used to determine whether it is an ELF file. This cannot be modified.
• 0x4 indicates the bit architecture, 0x5 is alignment, 0x6 is version, and 0x7 is OS/ABI. These cannot be modified.
• 0x10 indicates the file type (executable), and the byte at 0x12 indicates the architecture (x86). These cannot be modified.
• 0x18 to 0x1b indicate the entry point.
• 0x1c to 0x1f indicate the start address of the program segment, 0x2a to 0x2b indicate the size of the program segment, and 0x2c to 0x2d indicate the number of program segments.

In the program segment:

• The first 4 bytes are the offset, 0x4 to 0x7 are the virtual address, 0x8 to 0xb are the physical address, 0xc to 0xf are the file size, 0x10 to 0x13 are the memory size, and the remaining 8 bytes are flags and alignment, which can be ignored.
• It must be ensured that the virtual address plus the offset of the code segment in the file corresponds to the entry point address. For example, if virt = 0x500000 and offset(code) = 0x1b, then entrypoint = 0x50001b.

In summary, only the bytes from 0x20 to 0x29 and those after 0x2e in the header can be controlled. (Of course, the image above also successfully utilized the space from 0x1b to 0x1f by constructing certain instructions, but that's a later topic.)

To address the issue that the four bytes from 0x2a to 0x2d cannot be utilized, I chose to construct relevant instructions (or use jump instructions). Both options make full use of the available space.

After these operations, my program was compressed to 138 bytes.

Level 5 (Algorithm Modification)

Of course, the story still isn't over. I trimmed it a bit more, reducing it from 138 bytes to 131 bytes, and then climbed the rankings again.

But yesterday (December 8) morning, my opponent updated the record to 119 bytes. Actually, I had a 117-byte version in reserve at the time. Since I was nearing the limit of my assembly compression, I didn't rush to submit it.

This is the assembly code I previously had GPT-4 generate (though it underwent some optimization):

.section .text
.globl _start

_start:
    # Read the input string "xy zw"
    add $3, %al           # syscall number for read
    lea (%esp), %ecx     # buffer to store the input string
    mov $5, %dl           # number of bytes to read ("xy zw")
    int $0x80             # syscall

    # Convert first number from ASCII to integer
    movzbl (%ecx), %eax  # load first digit (x)
    sub $'0', %al         # convert from ASCII to integer
    imul $10, %eax        # multiply by 10
    inc %ecx              # move to next digit
    movzbl (%ecx), %edx  # load second digit (y)
    sub $'0', %dl         # convert from ASCII to integer
    add %edx, %eax        # add second digit to first digit
    mov %eax, %esi

    # Convert second number from ASCII to integer
    inc %ecx              # move to next digit
    inc %ecx              # move to next digit
    movzbl (%ecx), %eax  # load third digit (z)
    sub $'0', %al         # convert from ASCII to integer
    imul $10, %eax          # multiply by 10
    inc %ecx              # move to next digit
    movzbl (%ecx), %edx  # load fourth digit (w)
    sub $'0', %dl         # convert from ASCII to integer
    add %edx, %eax        # add second digit to first digit
    
    # Add the two numbers
    add %esi, %eax    # add num1 and num2

    # Convert result to ASCII (max 3 digits)
    mov $10, %bl          # divisor for conversion
convert_loop:
    xor %edx, %edx        # clear edx
    div %ebx              # divide eax by 10, result in eax, remainder in edx
    add $'0', %dl         # convert remainder to ASCII
    dec %esp              # move stack pointer for next digit
    inc %edi
    mov %dl, (%esp)       # store ASCII character on stack
    test %eax, %eax       # check if number is fully converted
    jnz convert_loop      # if not zero, continue loop

    # Prepare for write syscall
    lea (%esp), %ecx      # pointer to the sum (on the stack)
    mov %edi, %edx
    mov $1, %bl
    mov $4, %al          # syscall number for write
    int $0x80             # syscall

Then I felt there wasn't much room for optimization at the code level, so I rewrote the algorithm:

 mov  ecx, esp
 mov  dl, 8
 mov  al, 3
 int  0x80
 mov  al, byte ptr [ecx]
 sub  al, 0x60
 add  al, byte ptr [ecx + 3]
 imul ax, ax, 0xa
 add  al, byte ptr [ecx + 1]
 add  al, byte ptr [ecx + 4]
 sub  al, 0x60
 mov  dl, 2
 cmp  al, 0x64
 add  dl, 1
 mov  bl, 0x64
 div  bl
 add  al, 0x30
 mov  byte ptr [ecx], al
 add  ecx, 1
 shr  eax, 8
 mov  bl, 0xa
 div  bl
 add  ax, 0x3030
 mov  word ptr [ecx], ax
 mov  ecx, esp
 mov  ax, 4
 mov  bl, 1
 int  0x80

The first part of this code is easy to understand: it adds the low bits to the low bits and the high bits to the high bits, then subtracts 0x30 to convert ASCII to raw numbers.

The div instruction in the middle is a bit clever. Debugging with gdb reveals that div al places the quotient in the lower 8 bits and the remainder in the higher 8 bits. Once you understand that, the code becomes easy to follow.

An interesting point is that the previous code had a jump instruction for looping, but I accidentally deleted one line while debugging, which caused the output to always be 3 digits (with leading zeros if the number was shorter). Surprisingly, it still passed the tests. So I simply removed the loop logic altogether.

This brought the program down to 107 bytes.

Level 6 (Instruction Substitution)

This is an interesting aspect of x86 assembly. Since x86 assembly uses variable-length instructions, semantically identical instructions can be implemented in different ways, resulting in different machine code lengths.

• For example, when loading an immediate value, since the problem ensures the data range is <256, using the al register instead of eax as the destination can save 3 bytes.
• For example, replacing add eax, 1 with inc eax can save 2 bytes.
• For example, if there are unused registers available, replacing stack read/write instructions with register operations can save at least 2 bytes.
• For example, in the previous header, 05 04 00 00 00 actually disassembles to add eax, 4. Then, using dec eax can achieve the same functionality as mov al, 3, saving an additional byte.

In this challenge, I performed the following operations. Readers can look up how these assembly instruction substitutions save space in terms of byte count:

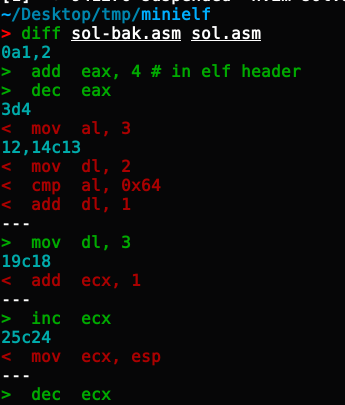
After applying these "clever tricks," the program size decreased from 107 bytes to 99 bytes. This is my final result.