(archived) Applied Cryptography Notes

Abbreviated as "Big Network Security and Data".

Overview of Cryptography

The four properties of modern cryptography: confidentiality, integrity, authentication, and non-repudiation.

Three periods: classical cryptography (algorithm secrecy), modern cryptography (key secrecy), and contemporary cryptography.

Attacks on cryptographic systems: ciphertext-only attack, known-plaintext attack, chosen-plaintext attack, chosen-ciphertext attack.

Kerckhoffs' principle: Security depends only on the secrecy of the key, not the algorithm. Otherwise, it is a "restricted cryptographic algorithm."

Security classifications: unconditional security, computational security, provable security.

Functions of cryptographic algorithms: encryption, hashing, digital signatures, identity authentication, key agreement.

Private keys are used for signing, public keys are used for verification.

Homework (p14):

1-1, 1-2, 1-4, 1-6, 1-7

Classical Cryptography

Monoalphabetic Substitution Cipher

Caesar

$c=m+k$

$m=c-k$

Affine Cipher

$k=(k_1,k_2)$

$c=k_{1}m+k_2$

$m=(c-k_2)k_1^{-1}(\mathrm{mod}26)$

Key Phrase Cipher

Place the key at the beginning, and arrange the remaining letters after the key to form the substitution table.

Disadvantages

Word frequency analysis.

Polyalphabetic Substitution Cipher

Vigenère

$c_i=m_i+k_i$

$m_i=c_i-k_i$

Hill Cipher

$C=K\cdot M$

$M=K^{-1}\cdot C(\mathrm{mod}26)$

where $C$ and $M$ are column vectors, and $K_n$ is the encryption matrix.

Advantages and Disadvantages:

• Resistant to ciphertext-only attacks; large key space.
• Vulnerable to known-plaintext attacks and chosen-plaintext attacks.

OTP (Vernam)

$c_i=m_i\oplus k_i$

$m_i=c_i\oplus k_i$

The key must not be reused, and it is theoretically unbreakable.

Playfair

Remove duplicate letters from the key, place them at the beginning, and append the remaining letters. Treat "i" and "j" as occupying the same cell. Arrange them into a 5×5 matrix.

Group the plaintext into pairs (denoted as p1, p2). Then:

• If they are in the same row, the ciphertext is the letter to the right of each plaintext letter (the rightmost wraps around to the first in the row).
• If they are in the same column, the ciphertext is the letter below each plaintext letter (the bottommost wraps around to the top in the column).
• If neither, take the opposite diagonal as the ciphertext, where each ciphertext letter shares the same row as its corresponding plaintext letter.
• If the two letters are the same (or only one remains), insert a predetermined letter (e.g., "x") in the middle (to the right).

Chained Cipher Algorithm

Uses the result of encrypting one plaintext as the encryption key for the next plaintext.

Disadvantage: Error propagation.

Substitution Cipher

Cyclic Permutation

The key specifies the permutation of positions.

It is a special case of the Hill cipher, belonging to the category of linear transformation ciphers.

Columnar Transposition Cipher

Fill the plaintext into a matrix row by row, and the key specifies the order in which columns are read.

Rotor Machine Cipher

Not tested.

Homework:

2.1 2.4 2.5 2.7 2.8 2.10 2.11 2.13 2.14 2.15

Block Cipher

Design Principles

• Diffusion Principle: Each bit of the plaintext should affect as many bits of the ciphertext as possible, and each bit of the ciphertext should be influenced by as many bits of the plaintext as possible.
• Confusion Principle: Even if an adversary obtains both the plaintext and the ciphertext, they should not be able to deduce any information about the key.
• Software Design: Use sub-blocks and simple operations.
• Hardware Implementation: Strive to use regular structures.

If $S^2=S$, it is an idempotent cryptosystem, such as affine ciphers, permutation ciphers, etc.

Iterative cryptosystems must be non-idempotent.

Typical Structures

• SPN Structure: Faster diffusion, but encryption and decryption are not similar.
• Feistel Structure: Encryption and decryption are similar, with slower diffusion (at least two rounds are required to change every bit of the input).

$L_{i+1}=R_i$

$R_{i+1}=L_i\oplus F(R_i,K_i)$

DES (Key Points)

• Security entirely depends on the confidentiality of the key.
• Key length is 64 bits (8 bits used for parity check).

Steps:

• Initial Permutation (IP) of the plaintext.
• $E$ expansion of $R_0$ to obtain $R_0(32\to 48)$: Divide $R_0$ into 8 blocks, denoted as $B_1$ to $B_4$, then prepend the last $B_4$ of the previous block to $B_1$, and append the first $B_1$ of the next block to $B_4$.
• Add parity bits to $K_0$ (multiple of 8), obtain C[0] and D[0] via $\mathtt{\text{PC-1}}$, left-shift once to get C[1] and D[1], and obtain the 48-bit $K_1$ via PC-2.
• $R_0\oplus K_1$
• $S$-box transformation $(48\to 32)$: Different blocks use different $S$-boxes. Take $B_2$ to $B_5$ as the row of the $S$-box, and $B_1{B}_6$ as the column of the $S$-box (big-endian). The value obtained from the lookup table serves as the key block. (Key Point)
• $P$-box transformation.
• XOR with $L_0$ to obtain $R_1$, completing one round of iteration.
• After 16 rounds of iteration, perform an inverse IP permutation.

Advantages:

• Encryption and decryption structures are identical.
• High strength.

Proof of complement symmetry:

For the $F$ function, $F(k,R)=PS(k\oplus E(R))=PS(\bar{k}\oplus E(\bar{R}))=F(\bar{k},\bar{R})$

Thus, the round function $Q_k(L,R)=(R,L\oplus F(k,R))=(R,L\oplus F(\bar{k},\bar{R}))$, and further $\overline{Q_k(L,R)}=(\bar{R},\bar{L}\oplus F(\bar{k},\bar{R}))=Q_{\bar{k}}(\bar{L},\bar{R})$

Let $D$ be the swap of left and right blocks, and $x=(L,R)$. Then the encryption function $E_{\bar{k}}(\bar{x})=D\cdot Q_{k_{16}}{Q}_{k_{15}}...Q_{k_1}(\bar{x})=D\cdot \overline{Q_{k_{16}}{Q}_{k_{15}}...Q_{k_1}(x)}=\overline{D\cdot Q_{k_{16}}{Q}_{k_{15}}...Q_{k_1}(x)}=\overline{E_k(x)}$

Improvement: Triple DES.

Block Cipher Modes of Operation

• ECB: Each block of plaintext is encrypted into the corresponding ciphertext block. The last incomplete block (less than 64 bits) is padded with a random string. (Essentially a large monoalphabetic substitution.)
• CBC (Commonly Used): The current plaintext block is XORed with the previous ciphertext block before encryption. The initial vector must be kept strictly confidential.
• CFB: Encryption is performed in units much smaller than the block size. The ciphertext depends on all previous plaintext.
• OFB: Feedback occurs within the block. (Vulnerable to tampering.)
• CTR: Allows parallel processing and precomputation, and can generate a good pseudorandom number sequence.

How to Choose:

• Security
• Efficiency
• Functionality

AES (Key Points)

Mathematical Foundations

Multiplication in the finite field $\mathrm{GF}(2^8)$: omitted.

x-multiplication: Since the modulus chosen for AES is 0x11b, i.e., $x^8+x^4+x^3+x+1$, when the high bit of the multiplier is 0, it is equivalent to a left shift; otherwise, it is equivalent to a left shift followed by an XOR with 0x1b.

Cross multiplication: Refers to the multiplication of two degree-4 polynomials in $\mathrm{GF}(2^8)$ modulo $x^4+1$. The process can be simplified using matrix multiplication. Specifically, for polynomials $\overline{a_3{a}_2{a}_1{a}_0}$ and $\overline{b_3{b}_2{b}_1{b}_0}$, the product $\overline{d_3{d}_2{d}_1{d}_0}$ is given by:

$$\left[\begin{array}{c}{d}_0\\ d_1\\ d_2\\ d_3\end{array}\right]=\left[\begin{array}{cccc}{a}_0& a_3& a_2& a_1\\ a_1& a_0& a_3& a_2\\ a_2& a_1& a_0& a_3\\ a_3& a_2& a_1& a_0\end{array}\right]\cdot \left[\begin{array}{c}{b}_0\\ b_1\\ b_2\\ b_3\end{array}\right]$$

Here, the dot product between terms corresponds to multiplication in $\mathrm{GF}(2^8)$ (using x-multiplication), and addition corresponds to XOR.

Steps

Key length: 128 bits.

• SubBytes: Lookup table substitution.
• ShiftRows: Cyclically shift the $i$-th row left by $i$ bytes.
• MixColumns (Key step): For each column, perform a cross multiplication, where $\overline{a_3{a}_2{a}_1{a}_0}$ is fixed as 3112H.
• AddRoundKey: XOR with the round key column by column.

Overall process:

AddRoundKey()

for i from 1 to 9:
  SubBytes()
  ShiftRows()
  MixColumns()
  AddRoundKey()

SubBytes()
ShiftRows()
MixColumns()

Other Symmetric Encryption Algorithms

• IDEA (Block size 64bit, Key length 128bit, Non-Feistel structure)
• RC6 (Block size 128bit, Key length 128, 192, 256bit, Feistel structure)
• SM4 (Block size 128bit, Key length 128bit, Asymmetric Feistel structure)

Asymmetric Encryption

Disadvantages of Symmetric Cryptography

• Poor system openness (how to transmit the key)
• Difficult key management: $n$ devices require $\frac{n(n-1)}{2}$ keys.
• Issues with digital signatures.

Characteristics of Public Keys

• Convenient key management with high openness
• High computational cost for encryption and decryption

Functions of a Public Key

• Conventional key distribution and negotiation
• Digital signatures
• Encryption and decryption (less efficient and not recommended for direct use)

RSA

Specific process: Omitted

Using the Chinese Remainder Theorem (CRT) to achieve fast computation in RSA

Example: Compute $m^d(\mathrm{mod}n)$, where $n=pq$, $p$ and $q$ are distinct primes, and $d$ is the private key.

Solution: Use Euler's theorem to compute $m^d(\mathrm{mod}p)$ and $m^d(\mathrm{mod}q)$ separately, then apply CRT to compute $m^d(\mathrm{mod}n)$.

Miller-Rabin

Fermat's Little Theorem is a necessary condition for a modulus to be prime.

Quadratic Residue Theorem: If $p$ is an odd prime, then the solutions to $x^2\equiv 1(\mathrm{mod}p)$ are only $x\equiv 1$ or $x\equiv -1$.

Pseudocode:

# false rate: 1 - 4^(-s)
def WITNESS(a, n):
  if pow(a, n-1, n) != 1:
    return FALSE
  else while n % 2 == 0:
    n /= 2
    if pow(a, n-1, n) != 1 or -1:
      return FALSE
  return TRUE

for i from 1 to s:
  if WITNESS(integers[i], n) == FALSE
    return NOT_PRIME
return PRIME

ElGamal

Description

System parameters: $p,\alpha \in {\mathbb{Z}}_p^{\ast }$.

Select a private key $x_A$, and the public key is $y_A={\alpha }^{x_A}(\mathrm{mod}p)$.

Encryption:

• Choose a random number $k\in [2,p-2]$.
• $c_1={\alpha }^k(\mathrm{mod}p)$
• $c_2=m\cdot y_A^k(\mathrm{mod}p)$

Decryption:

• $m=c_2\cdot (c_1^{x_A}{)}^{-1}(\mathrm{mod}p)$

Features

• Non-deterministic (dependent on k)
• Ciphertext space is larger than the plaintext space

ECC

SM2 also employs the elliptic curve cryptography system.

Elliptic Curves over the Real Number Field

The equation $y^2=x^3+ax+b$ can be denoted as $E(a,b)$, or simply $E$.

If points $P$, $Q$, and $R$ are collinear, the additive identity $O$ is defined as $O=P+Q+R$. For any point $P$ on the curve, $P+O=P$.

It follows that the additive inverse of a point has the same $x$-coordinate but opposite $y$-coordinate.

Thus, the addition operation is defined as follows: draw the line through $P$ and $Q$, which intersects $E$ at $R$; then $-R$ is the result of $P+Q$. The doubling operation can be defined analogously (omitted here). It can be shown that this addition satisfies the commutative and associative laws.

From an algebraic perspective, $P+Q=(x_3,y_3)=({\lambda }^2-x_1-x_2,\lambda (x_1-x_3)-y_1)$, where $\lambda$ is the slope of the line. If $P$ and $Q$ coincide, then $\lambda =\frac{3x^2+a}{2y}$.

Elliptic Curves over Finite Fields

Focus on $\mathrm{GF}(p)$; $\mathrm{GF}(2^n)$ is not included in the exam.

$y^2=x^3+ax+b(\mathrm{mod}p)$ can be denoted as $E_p(a,b)$, abbreviated as $E_p$.

It can be proven that an elliptic curve over a finite field forms a cyclic group under the + operation.

The definition of addition involves taking the corresponding coordinates modulo $p$, and doubling is similar.

Example: Find the number of points in $E_{11}(1,6)$:
Answer: There are 13 points in total (don't forget the point at infinity $O$!).

ElGamal on Elliptic Curves

Let $\mathrm{ord}(P)$ be the smallest integer $n$ such that $nP=O$.

ECDLP: Given $\alpha$ and $\beta$, finding $k\in [0,\mathrm{ord}(\alpha )-1]$ such that $k\alpha =\beta$ is computationally hard.

Similar to the Discrete Logarithm Problem (DLP), point addition can be analogized to modular multiplication, and point doubling to exponentiation.

System parameters: $E(a,b)$, base point $G$ (with order $n$).

Key generation: Select a private key $d_A$, and compute the public key $P_A=d_{A}G$.

Encryption:

• Map the plaintext message $m$ to a point $P_m$.
• Select a random number $k\in [2,n-1]$.
• $c_1=kG$
• $c_2=P_m+k{P}_A$

Decryption:

• $P_m=c_2-d_A{c}_1$
• Apply the inverse mapping to $P_m$ to recover $m$.

Menezes-Vanstone

Primarily addresses the problem of mapping plaintext $m$ to $P_m$.

System parameters: $E(a,b)$, base point $G$ (with order $n$).

Key generation: Select private key $d_A$, public key is $P_A=d_{A}G$.

Encryption:

• $m=(m_1,m_2)$
• Select a random number $k\in [2,n-1]$
• $c_1=kG$
• $Y=(y_1,y_2)=k{P}_A$
• $c_2=y_1{m}_1(\mathrm{mod}p)$
• $c_3=y_2{m}_2(\mathrm{mod}p)$

Decryption:

• $d_A{c}_1=(z_1,z_2)$ (Note that $d_A{c}_1=k{P}_A$, so $y_1=z_1,y_2=z_2$)
• $m_1=c_2{z}_1^{-1}(\mathrm{mod}p)$
• $m_2=c_3{z}_2^{-1}(\mathrm{mod}p)$
• Obtain $m$ from $(m_1,m_2)$

Example: Let base point $G$ in $E_{11}(1,6)$ be $(2,7)$, key $d=7$, plaintext be $(9,1)$, random number $k=6$, compute the ciphertext.

Solution: Compute public key $P_A=dG=7(2,7)=(7,2)$

$c_1=6G=(7,9)$

$Y=k{P}_A=kdG=42G=3G=(8,3)$

$c_2=8\times 9=6(\mathrm{mod}p)$

$c_3=3\times 1=3(\mathrm{mod}p)$

Therefore, the ciphertext is $((7,9),6,3)$

Code implementation (done while working on homework at night)

# ECC en&decrypt in GF(p)
# 4/24/2023 junyu33
import gmpy2
a = 1
b = 6
p = 11
G = [2, 7]
d_A = 5
def Add(A: list, B: list) -> list:
    lamb = 0
    if A == B:
        lamb = (3*A[0]*A[0]+a)*gmpy2.invert(2*A[1], p) % p
    else:
        lamb = (B[1]-A[1])*gmpy2.invert(B[0]-A[0], p) % p
    s = (lamb**2 - A[0] - B[0]) % p
    t = (lamb*(A[0]-s) - A[1]) % p
    return [s,t]

def Mult(X: list, t: int) -> list:
    R = X
    t = t - 1
    while t:
        if t & 1:
            R = Add(R, X)
        X = Add(X, X)
        t >>= 1
    return R

def enc(M: list, G: list, k: int):
    c_1 = Mult(G, k)
    P_A = Mult(G, d_A)
    Y = Mult(P_A, k)
    c_2 = Y[0] * M[0] % p
    c_3 = Y[1] * M[1] % p
    print(c_1, c_2, c_3)

def dec(c_1: list, c_2: int, c_3: int):
    Y = Mult(c_1, d_A)
    z_1 = Y[0]
    z_2 = Y[1]
    m_1 = c_2 * gmpy2.invert(z_1, p) % p
    m_2 = c_3 * gmpy2.invert(z_2, p) % p
    print(m_1, m_2)

enc([7,9],G,3)

Hash

SHA-1 (Cracked)

big-endian

2**64-1 -> 160 bit

Steps

• Padding: origin + 1000...000 (length 448 - len % 512) + len
• Initial MD buffer: A = 67452301, B = EFCDAB89, C = 98BADCFE, D = 10325476, E = C3D2E1F0
• Process the message in 512-bit blocks:
  A, B, C, D, E ← [(A << 5) + f_t(B, C, D) + E + W_t + K_t], A, (B << 30), C, D
  A total of 80 rounds are performed, where:
  • $f_t$ is the logical function, defined as:
    (B & C) | (~B & D), B ^ C ^ D, (B & C) | (B & D) | (C & D), B ^ C ^ D for rounds 1–20, 21–40, 41–60, and 61–80, respectively.
  • $W_t$ is the 32-bit sub-message block W[t]. The first 16 entries correspond directly to the 512-bit input block. Subsequent entries (for t = 16 to 79) are computed as:
    W[t] = (W[t-16] ^ W[t-14] ^ W[t-8] ^ W[t-3]) << 1
  • $K_t$ is a fixed constant (for $1\le t\le 4$):
    5A827999, 6ED9EBA1, 8F1BBCDC, CA62C1D6
  • The first 20 rounds use $t=1$, the next 20 use $t=2$, and so on.
• The initial A, B, C, D, E values are added to the final A', B', C', D', E' values to form the new buffer. After processing all blocks, the resulting buffer is the SHA-1 hash.

Birthday Attack

If the size of the message space is $N$, then approximately $\sqrt{N}$ randomly selected messages are required to have a 50% probability of producing a collision.

SM3

A domestic commercial cryptographic hash function.

Operates on 512-bit blocks and produces a 256-bit output.

Used in smart electricity meters and TPM 2.0.

Message Authentication

Classification of Message Authentication Code (MAC):

• Encryption Techniques
• Hash Functions
• HMAC Algorithm (Keyed One-Way Hash Function)

Digital Signature

RSA

The sender uses $s_A=m^d(\mathrm{mod}n)$ to sign.

The receiver uses $m=s_A^e(\mathrm{mod}n)$ for verification.

ElGamal

Initialization: $e_A={\alpha }^{d_A}(\mathrm{mod}p)$

Signature Transformation:

• Select a random number $k$ that is coprime with $p-1$.
• Signature:
  • $r={\alpha }^k(\mathrm{mod}p)$
  • $s=(H(M)-d_{A}r)k^{-1}(\mathrm{mod}p-1)$, where $H$ is a one-way hash function.
  • Send $(r,s)$.
• Verification:
  • Compute $H(M)$.
  • Compute $e_A^r{r}^s(\mathrm{mod}p)$ and ${\alpha }^{H(M)}(\mathrm{mod}p)$. If they are equal, the signature is valid.

Note: $k$ must not be leaked. The same applies to the encryption part.

DSA

$p$, $q$, and $g$ are public, where $q$ is a prime factor of $p-1$, and $g=h^{(p-1)/q}(\mathrm{mod}p)$.

A random $x$ is selected as the private key, and the public key is $y=g^x(\mathrm{mod}p)$.

Signature transformation:

• Signing:
  • Select $k\in (0,q)$.
  • $r=(g^k(\mathrm{mod}p))(\mathrm{mod}q)$.
  • $s=k^{-1}(H(m)+xr)(\mathrm{mod}q)$.
  • Send $(r,s)$.
• Verification:
  • $w=s^{-1}(\mathrm{mod}q)$.
  • $u_1=H(m)w(\mathrm{mod}q)$.
  • $u_2=rw(\mathrm{mod}q)$.
  • $v=(g^{u_1}{y}^{u_2}(\mathrm{mod}p))(\mathrm{mod}q)$. If $v=r$, the signature is valid.

ECDSA

$E(F_p),G,n$ are the system parameters.

Randomly select $d\in (1,n)$ as the private key, and $Q=dG$ as the public key.

• Signing:
  • Choose a random number $k\in (1,n-1)$
  • $kG=(x_1,y_1)$
  • $r=x_1(\mathrm{mod}n)$
  • $s=k^{-1}(h(M)+dr)(\mathrm{mod}n)$
  • Send $(r,s)$
• Verification:
  • $u_1=h(M)s^{-1}(\mathrm{mod}n)$
  • $u_2=r{s}^{-1}(\mathrm{mod}n)$
  • $X(x_2,y_2)=u_{1}G+u_{2}Q$
  • $v=x_2(\mathrm{mod}n)$; if $v=r$, accept the signature.

Special Signatures

• Undeniable Signatures
• Blind Digital Signatures
• Group Signatures

Key Management Technologies

Diffie-Hellman (Asymmetric, only used for key exchange between two users)

System parameters: $p,\alpha$

• Alice selects a private $r_a$ and computes $s_a={\alpha }^{r_a}(\mathrm{mod}p)$
• Bob selects a private $r_b$ and computes $s_b={\alpha }^{r_b}(\mathrm{mod}p)$
• Both parties exchange $s_a$ and $s_b$
• Alice computes $s_b^{r_a}(\mathrm{mod}p)$
• Bob computes $s_a^{r_b}(\mathrm{mod}p)$

Clearly, the two computed values are equal, and the key agreement is completed.

Vulnerable to man-in-the-middle attacks.

Shamir's Threshold Scheme

System parameters: $k,n,q$

Secret: $s,a_1,a_2,\dots ,a_{k-1}$

A secret polynomial can be constructed as follows:

$$f(x)=s+a_{1}x+a_2{x}^2+\cdots +a_{k-1}{x}^{k-1}$$

The key distributor calculates $f(x_i)$ for each participant based on their key $x_i$ and distributes the corresponding value to them.

Using Lagrange interpolation, the secret polynomial can only be reconstructed by any subset of $\ge k$ participants. The process is as follows:

$$f(x)=\sum _{i=1}^{k}f(x_i)\prod _{j=1,j\ne i}^k\frac{x-x_j}{x_i-x_j}(\mathrm{mod}q)$$

Specifically, when $x=0$, the secret $s$ can be computed:

$$s=f(0)=(-1{)}^{k-1}\sum _{i=1}^{k}f(x_i)\prod _{j=1,j\ne i}^k\frac{x_j}{x_i-x_j}(\mathrm{mod}q)$$

Shortcomings:

• Fixed threshold value
• The secret distributor knows the participants' shadows
• Unable to prevent fraud by the secret distributor or participants

Identity Authentication Technology

Concepts, Threats, and Attack Methods

Challenge–Response Authentication:

• Additional communication overhead
• Prevents replay attacks by the claimant but not by the verifier: requires mutual authentication and timestamps.

S/Key One-Time Password Authentication:

• Prevents replay attacks
• Vulnerable to small number attacks (intercepting the server's seed and iteration value, modifying it to a smaller iteration value sent to the user, intercepting the user's password, and computing a larger iteration value)
• Lacks integrity protection mechanisms

Zero-Knowledge Proof Protocol

Let $n=p\times q$, and assume that Alice knows the factors of $n$. If Alice wants to convince Bob that she knows the factors without revealing them, she can perform the following steps:

• Bob randomly selects $x$, computes $y=x^4(\mathrm{mod}n)$, and sends $y$ to Alice.
• Alice computes $z=\sqrt{y}(\mathrm{mod}n)$ and sends $z$ to Bob.
• Bob verifies whether $z=x^2(\mathrm{mod}n)$ holds.
• If the verification succeeds multiple times in repetition, it proves that Alice indeed knows the factors of $n$.

The theoretical foundation lies in the fact that the difficulty of computing $\sqrt{y}(\mathrm{mod}n)$ is equivalent to factorizing $n$.

Kerberos Authentication

Uses a symmetric key system, with authentication services provided by a trusted third party.

Distributes shared keys to communicating parties through tickets.

Secure Communication

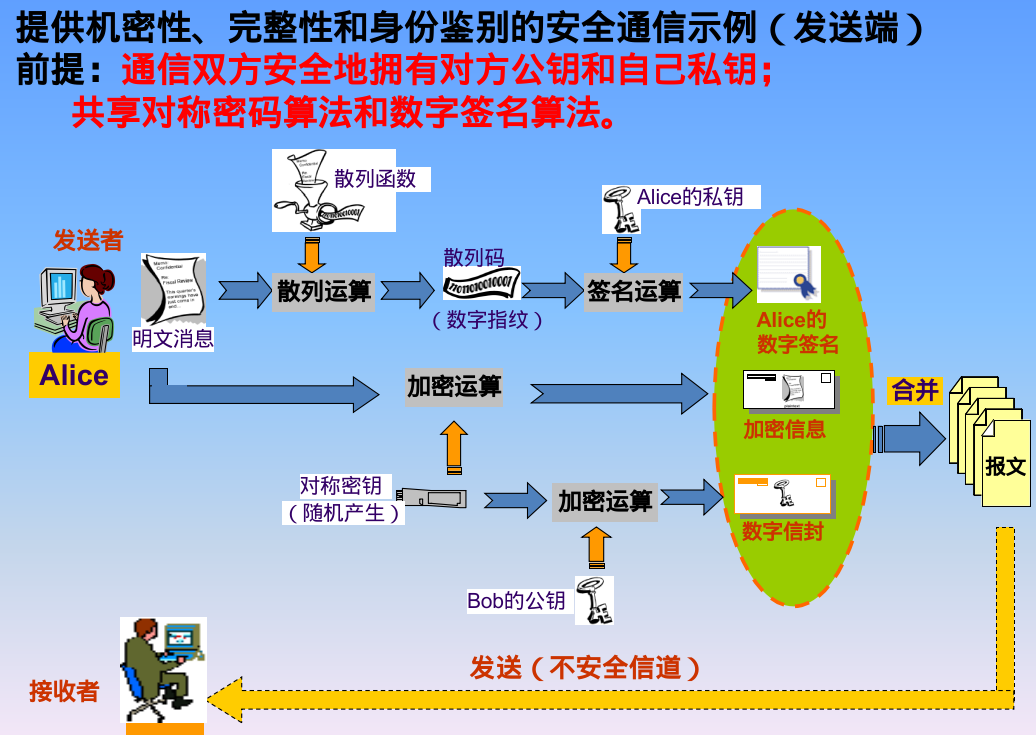
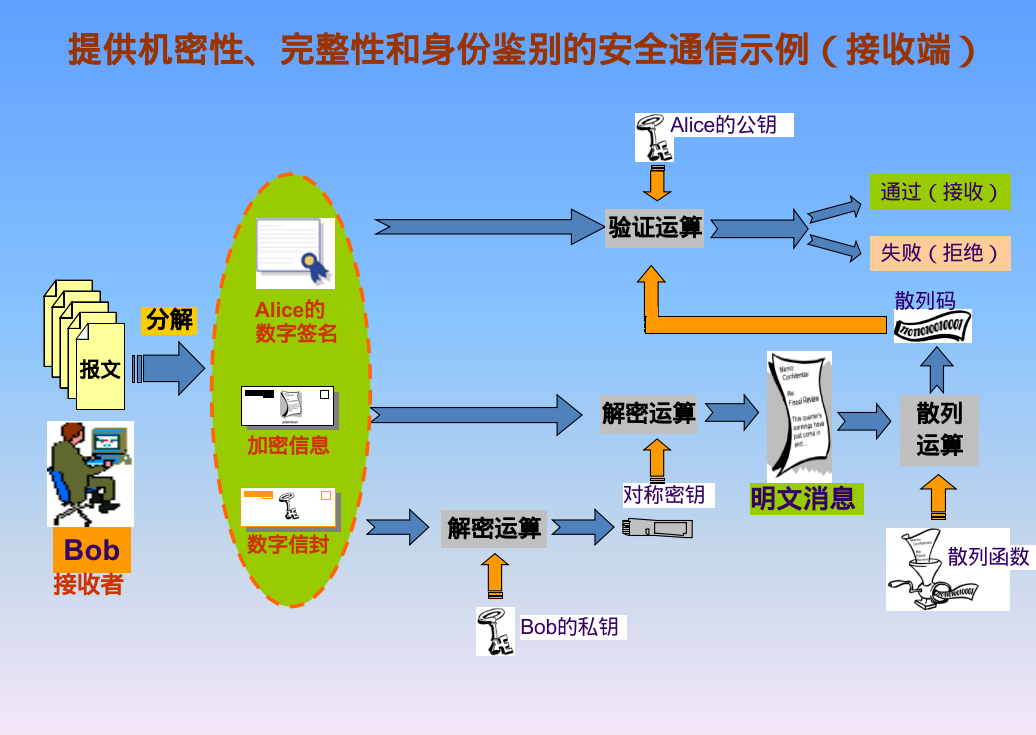
Pseudocode:

Sender:

# send.py
# Example usage:
with open("public_key_B.pem", "rb") as f:
  public_key_B = RSA.import_key(f.read())

with open('data', 'rb') as f:
  data = f.read()

# Party A encrypts the data and signs it
ciphertext = encrypt(data, key)
signature = sign(data, private_key_A)

# Party A encrypts the key using the public key of party B
encrypted_key = encrypt_key(key, public_key_B)

with open('encrypted_key', 'wb') as f:
  f.write(encrypted_key)

with open('ciphertext', 'wb') as f:
  f.write(ciphertext)

with open('signature', 'wb') as f:
  f.write(signature)

with open('public_key_A.pem', 'wb') as f:
  f.write(public_key_A.export_key('PEM'))

Receiver:

# receive.py
with open('public_key_A.pem', 'rb') as f:
  public_key_A = RSA.import_key(f.read())
with open('encrypted_key', 'rb') as f:
  encrypted_key = f.read()

with open('signature', 'rb') as f:
  signature = f.read()

with open('ciphertext', 'rb') as f:
  ciphertext = f.read()

# Party B decrypts the key and uses it to decrypt the data
key = decrypt_key(encrypted_key, private_key_B)
decrypted_data = decrypt(ciphertext, key)
with open('decrypted_data', 'wb') as f:
  f.write(decrypted_data)

# Party B verifies the signature of party A
is_valid = verify_signature(decrypted_data, signature, public_key_A)

if is_valid:
  print("The signature is valid")
else:
  print("The signature is not valid")

Stream Cipher Fundamentals

Also known as stream ciphers, they belong to the symmetric cryptosystem and are suitable for hardware implementation.

Classification

• Synchronous Stream Ciphers: The state of the memory element is independent of the plaintext or ciphertext, with no error propagation but requiring synchronization.
• Self-Synchronizing Stream Ciphers: The keystream generation is related to the ciphertext, featuring limited error propagation and self-synchronization.

LFSR

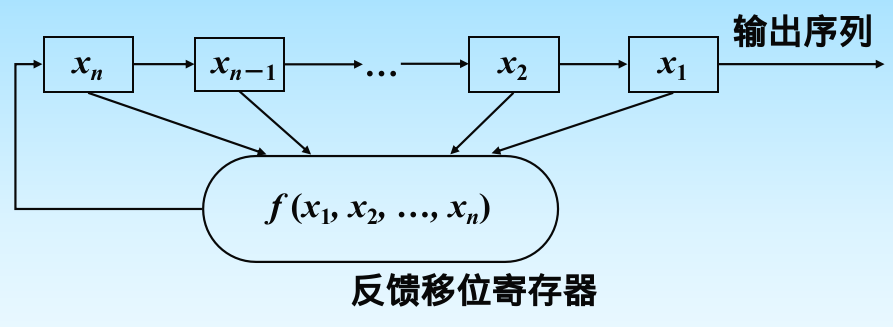
Note that the shift direction is from high-order bits to low-order bits, where $x_1$ is the output, and the value of $f$ becomes the next $x_n$.

The properties are entirely determined by the feedback function. The period $T$ of an $n$-stage LFSR satisfies $T\le 2^n-1$.

Stream cipher generators based on LFSR include:

• Geffe generator
• Clock-controlled generator
• Alternating step generator

RC4

Two algorithms: Key Scheduling Algorithm (KSA) and Pseudo-Random Generation Algorithm (PRGA).