How to get the "lucky money" red packets correctly

Note: This article only analyzes the algorithm of WeChat's "Lucky Money" red packets and identifies the optimal position for grabbing them. It does not aim to help readers profit from WeChat red packets.

Background

During the Spring Festival, I formed a red packet group with three other family members (four people in total). We agreed to participate in red packet grabbing activities every day after lunch and during prime time in the evening, with the following rules:

Send a "Lucky Money" red packet with a total value of 200 yuan, divided into 4 shares.

The person who gets the largest amount sends the next red packet.

Each round lasts 20 minutes, and the last person with the largest amount sends the first red packet the next day. (The first red packet on the first day is sent by the group owner.)

Due to my fast hand speed, I almost always managed to grab the first red packet every time. Then, one day, I ended up with the largest amount five times in a row and, unsurprisingly, lost 800+ yuan in that round. So the next day, I changed my strategy and waited for 5 seconds after the red packet appeared before grabbing it. That day, I won 200+ yuan in both rounds—it seemed my strategy was correct. My daily wins and losses indeed had some relationship with the position at which I grabbed the red packet.

Therefore, with some basic programming knowledge, I decided to simulate the red packet grabbing process using a computer to calculate, under the condition of a sufficiently large number of red packet grabs:

The probability of getting the largest amount at each position.

The expected win/loss outcome at each position.

Implementation

Lucky Money Red Envelope Algorithm

After researching online, I found that WeChat's lucky money amount distribution is implemented as follows.

We assume the total amount is $W$ , and the number of participants is $N$ . Then:

The range for the first red envelope amount $x_{1}$ is $[0.01, \frac{W}{N} * 2]$ .

The range for the second red envelope amount $x_{2}$ is $[0.01, \frac{W - x_{1}}{N - 1} * 2]$ .

The range for the third red envelope amount $x_{3}$ is $[0.01, \frac{W - x_{1} - x_{2}}{N - 2} * 2]$ .

......

The ranges for the second-to-last red envelope $x_{N - 1}$ and the last red envelope $x_{N}$ are both $[0.01, W - \sum_{i = 1}^{N - 2} x_{i}]$ .

Here, $x_{i}$ is uniformly randomized within the above ranges.

As we can see, the amounts of subsequent red envelopes are calculated in real-time based on the sum of the amounts already taken by previous participants. This approach eliminates the need for preprocessing the amounts inside the red envelope. For a communication platform like WeChat, which serves billions of users, this saves significant time and space overhead.

However, the consequence of this method is that although the mathematical expectation of the amount received is equal regardless of the order (though I cannot prove it), the variance of the possible amounts differs for each position. Generally, the variance of possible amounts increases as the order becomes later (which is why larger amounts tend to appear in later positions).

Before researching WeChat's algorithm, I had conceived a preprocessing-required amount distribution algorithm, with the following idea:

We assume the total amount is $W$ , and the number of participants is $N$ . Then:

Imagine a line segment of length $W$ , and randomly select $N - 1$ points on it. We name these points from left to right as $p_{1}$ to $p_{N - 1}$ .

The distributed amounts are:

$x_{1} = p_{1}$

$x_{i} = p_{i} - p_{i - 1}$ , where $i \in [2, n - 1]$

$x_{n} = W - p_{N - 1}$

The editor believes that this approach ensures fairness for everyone.

Writing Code and Testing

Based on the above ideas, I wrote the following C++ code.

(Why not use Python? Because generating $10^{6}$ random numbers in Python is too slow.)

#include <iostream>
#include <random>
#include <ctime>
#include <algorithm>
#define PERSON_MAX 100
#define INI_BALANCE 0
//#define NUM_PERSON 4
int NUM_PERSON;
#define NUM_ENV 200
//#define ITER_NUM 1000000
int ITER_NUM;
int MODE;
using namespace std;
double balance[PERSON_MAX], money[PERSON_MAX];
int num_first[PERSON_MAX];
default_random_engine f(time(NULL));
uniform_real_distribution<double> rnd(0, 1);
void init() {
	//	for(int i = 0; i < 4; i++)
	//		cout << rnd(f) << endl;
	cout << "Please enter the number of people grabbing red packets (less than 100)" << endl;
	cin >> NUM_PERSON;
	cout << "Please enter the number of red packets distributed (less than one million)" << endl;
	cin >> ITER_NUM;
	cout << "Please select the red packet generation rule: 1.WeChat rule, 2.My rule" << endl;
	cin >> MODE;
	for(int i = 0; i < NUM_PERSON; i++) {
		balance[i] = INI_BALANCE;
	}
}
void rand1() {
	double money_left = NUM_ENV;
	for(int i = 0; i < NUM_PERSON - 1; i++) {
		money[i] = rnd(f) * money_left / (NUM_PERSON - i) * 2;
		money_left -= money[i];
	}
	money[NUM_PERSON - 1] = money_left;
}
double pin[PERSON_MAX];
void rand2() {
	for(int i = 0; i < NUM_PERSON - 1; i++) {
		pin[i] = rnd(f) * NUM_ENV;
	}
	sort(pin, pin + NUM_PERSON - 1);

	money[0] = pin[0];
	for(int i = 1; i < NUM_PERSON - 1; i++) {
		money[i] = pin[i] - pin[i - 1];
	}
	money[NUM_PERSON - 1] = NUM_ENV - pin[NUM_PERSON - 2];
}
int gen(int who_first, int mode) {
	balance[who_first] -= NUM_ENV;

	if(mode == 1) rand1();
	else rand2();

	double max_money = -1.0;
//	double min_money = 10000.0;
	for(int i = 0; i < NUM_PERSON; i++) {
		balance[i] += money[i];
		if(money[i] > max_money) {
			max_money = money[i];
			who_first = i;
		}
//		if(money[i] < min_money) {
//			min_money = money[i];
//			who_first = i;
//		}		
	}
	num_first[who_first]++;
	return who_first;
}
void out() {
	printf("After %d rounds of grabbing red packets, the probability that the person who always grabs the i-th packet has the best luck:\n", ITER_NUM);
	for(int i = 0; i < NUM_PERSON; i++) {
		printf("%lf", 100.0 * num_first[i] / ITER_NUM);
		cout<<"% ";
	}
	printf("\n\n");
	//who is the luckiest
	printf("After %d rounds of grabbing red packets, the expected win/loss per round for the person who always grabs the i-th packet:\n", ITER_NUM);
	for(int i = 0; i < NUM_PERSON; i++) {
		printf("%lf ", balance[i] / ITER_NUM);
	}
	//who is the richest
}
int main()
{
	init();
	int who_first = 0;
	for(int i = 0; i < ITER_NUM; i++) {
		who_first = gen(who_first, MODE);
	}
	out();
	return 0;
}

First, I conducted an experiment based on my family's situation, and the results are as follows:

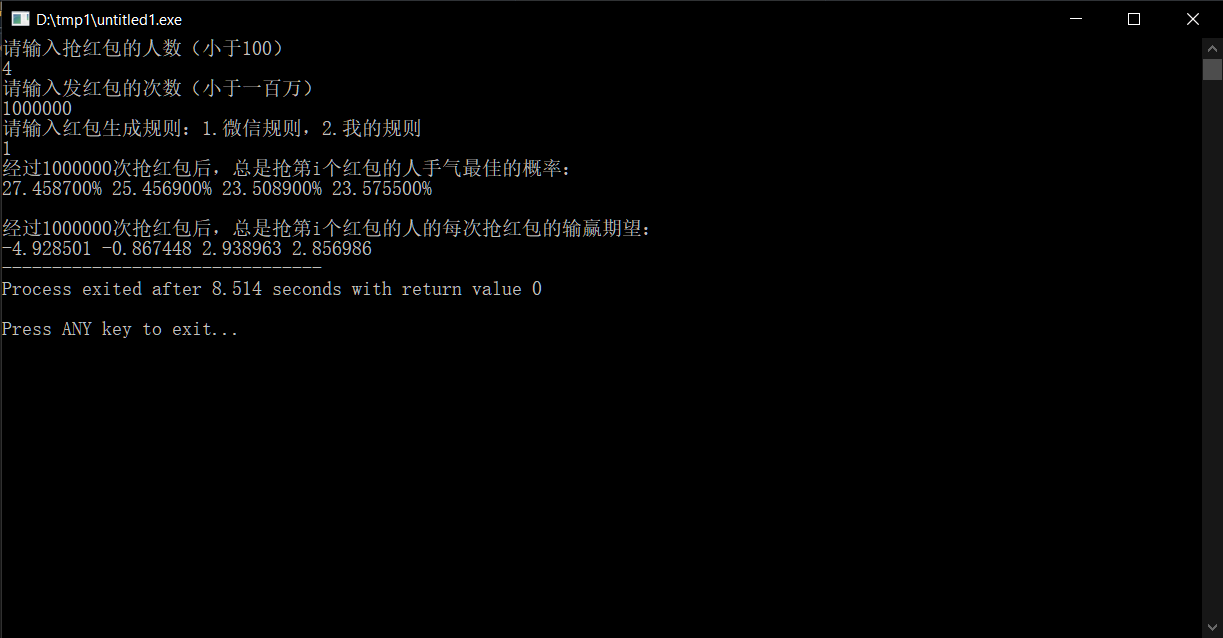
As can be seen, the person who grabs the red packet first has about a 27.4% chance of having the best luck, which is about 3.9% higher than the last two participants. Although this number may seem small, in just 20 minutes, at least 30 red packets can be distributed, accumulating a difference of about 200 yuan in red packet amounts.

Looking at the expectations, the person who grabs the red packet first loses nearly 5 yuan on average per round. Multiplied by the number of red packets in a round of "red packet rain," this amounts to roughly 150–200 yuan, which aligns with the probability-based calculation.

On the other hand, the last two participants to grab red packets have the lowest (or worst) performance in terms of both the probability of having the best luck and the expected winnings, and their positions are equivalent.

Extended Thinking

Increasing the Number of Participants

So, what happens if the number of people grabbing red packets isn't 4, but a large family (say, 20 people)?

The results were beyond my expectations.

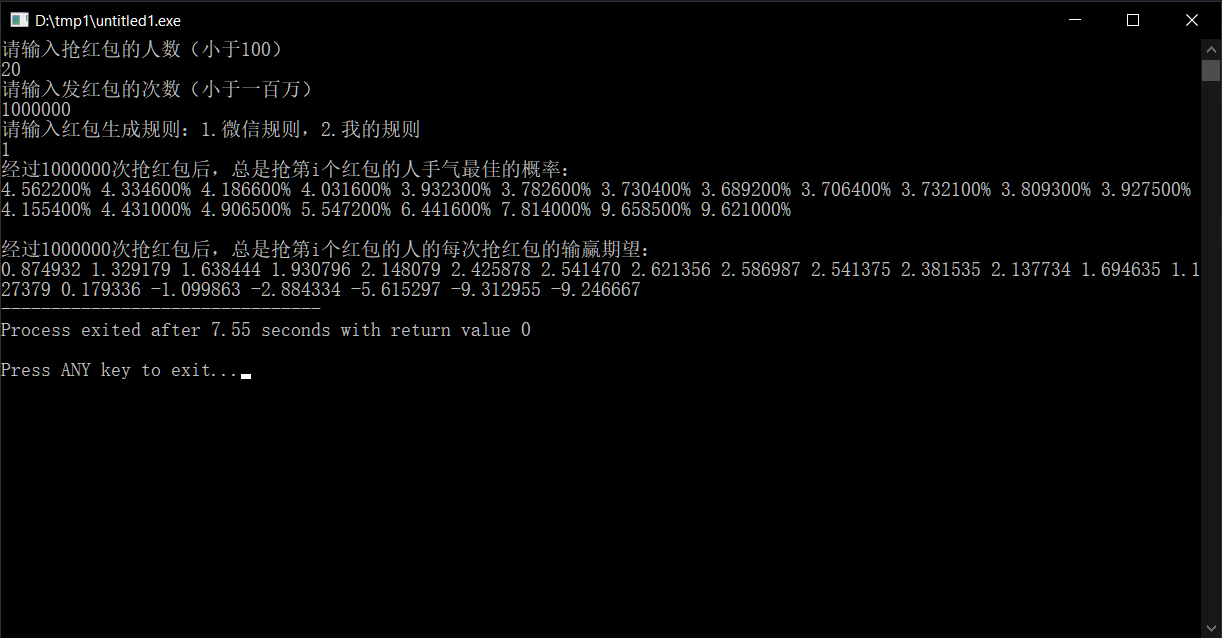
As we can see, the probability of being the luckiest starts at 4.65% for the first person, drops to 3.69% for the 8th person, then rapidly rises to 9.64% (on average) for the last two participants—nearly twice the average probability of 5%.

Meanwhile, the expected gain first increases and then decreases, with the last five participants starting to lose money.

Even with 100 people grabbing red packets, the last two still have an 8% chance of being the luckiest, but their expected loss increases to 14 yuan.

Improved Rules

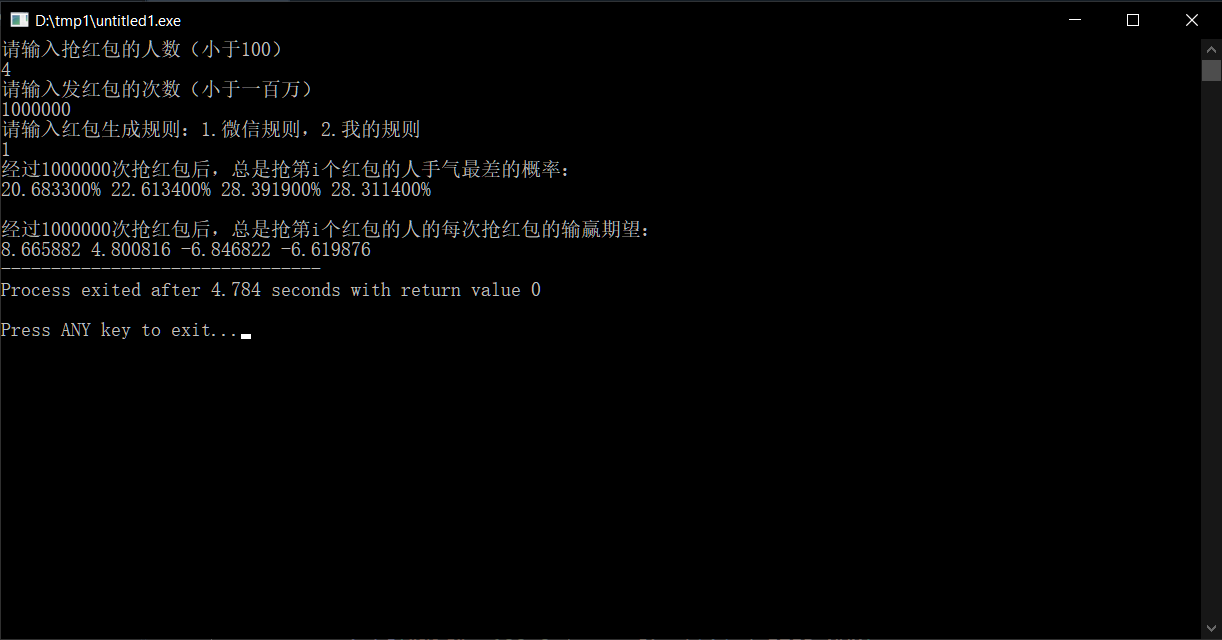
What if the person who grabs the least amount sends the next red packet?

When the number of participants is small, the earlier grabbers are less likely to get the worst luck and win more than the previous 4th participant, which aligns with our intuition.

When the number of participants is large, the trend of the worst luck and the expected gains or losses remain consistent with the small-group scenario. However, the last two participants lose significantly less than the previous $9.2$ to $9.3$ .

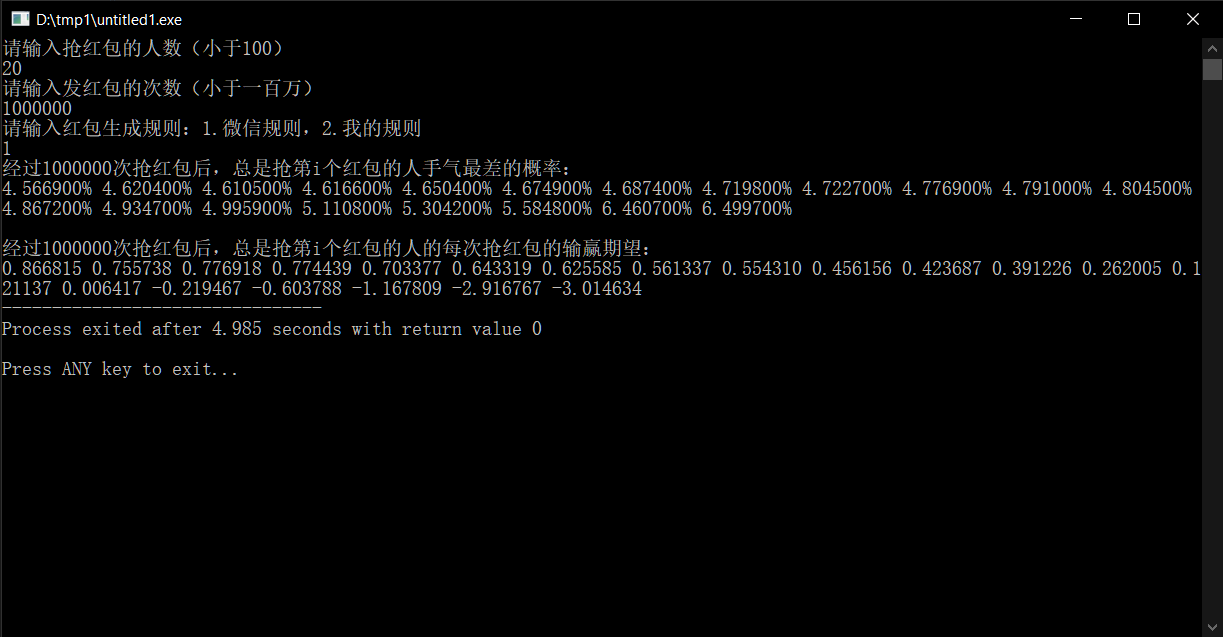
Algorithm Adjustment

Finally, let's see whether my algorithm is actually fair.

Here are the results with fewer participants:

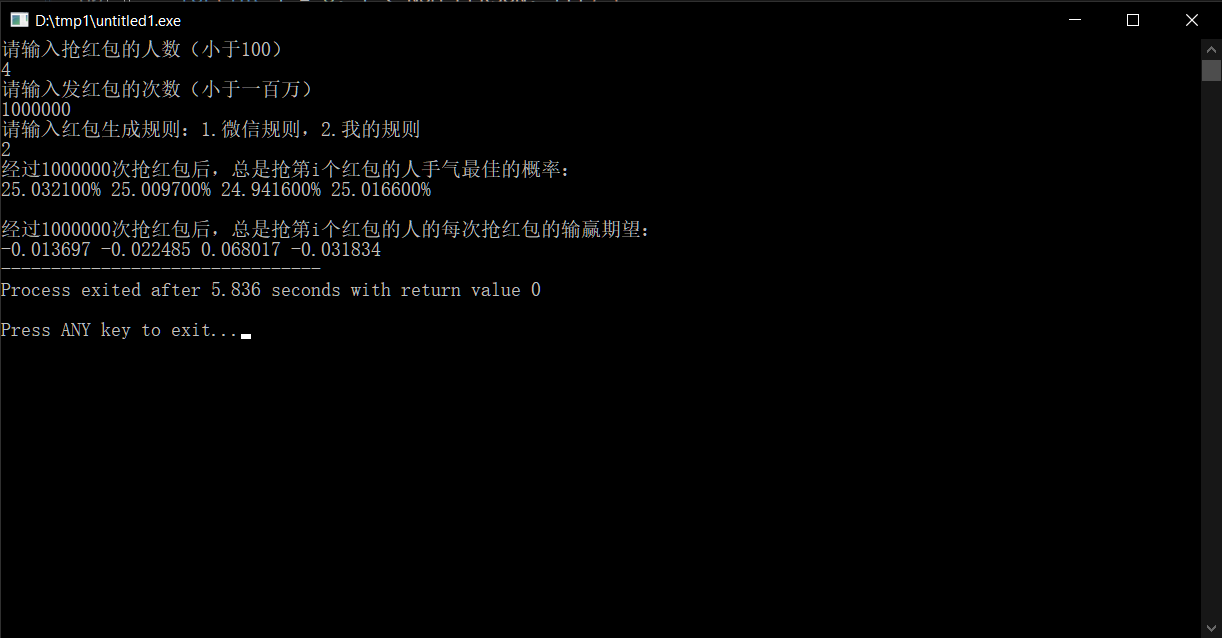
And here are the results with more participants:

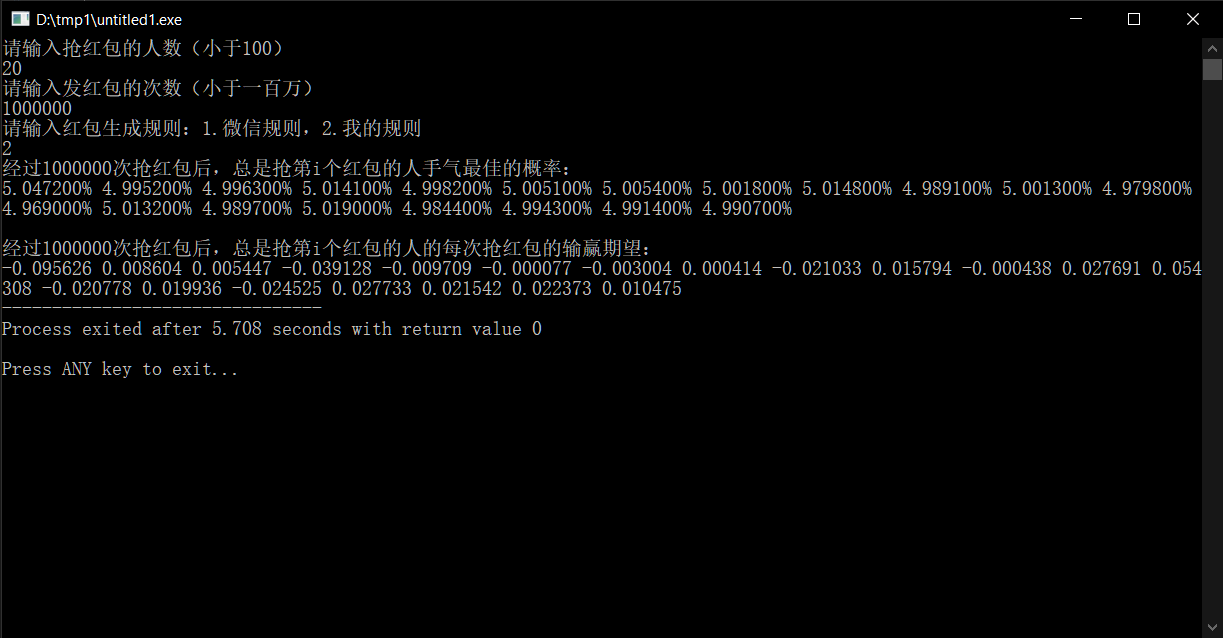
As we can see, the expected win/loss per round stabilizes within a few cents, which can be considered essentially fair.

Afterword

After finalizing the program, I shared my findings with my parents. That afternoon, during the red packet grabbing activity, my father consistently waited until the last moment to grab a packet, while I had no choice but to randomly join within the first three participants.

In the end, my father made a profit of 249 yuan, while I lost 253 yuan. It seems that figuring out the winning strategy didn't actually help me win money after all qwq.