csapp Binary Bomb Lab
solution
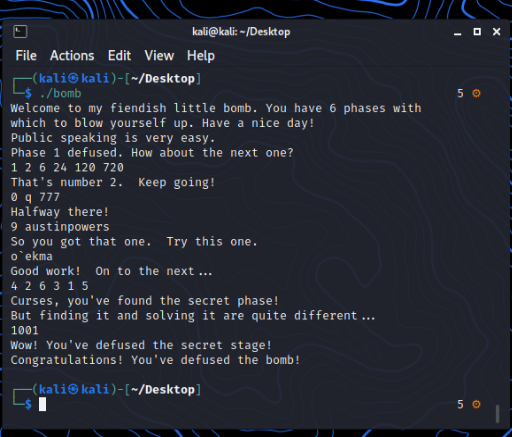
A nice reverse-engineering challenge: seven subtasks that gradually increase in difficulty, making it very suitable for beginners.
Thought Process Analysis
The following steps were carried out using IDA 7.5. I believe anyone interested in this problem probably has IDA at hand.
(Of course, the author's original intent was for you to read the assembly and debug with gdb—that would surely lead to hair loss.)
main function logic is very simple: the program provides file input (with argument 1) and standard input (no argument). Next, you need to answer six questions (phases). If any one of them is wrong, the bomb will explode.
I will now analyze it phase by phase.
phase_1
int __cdecl phase_1(int a1)
{
int result; // eax
result = strings_not_equal((_BYTE *)a1, "Public speaking is very easy.");
if ( result )
explode_bomb();
return result;
}
String comparison—just input:
Public speaking is very easy.
phase_2
int __cdecl phase_2(char *s)
{
int i; // ebx
int result; // eax
int v3[6]; // [esp+10h] [ebp-18h] BYREF
read_six_numbers(s, (int)v3);
if ( v3[0] != 1 )
explode_bomb();
for ( i = 1; i <= 5; ++i )
{
result = v3[i - 1] * (i + 1);
if ( v3[i] != result )
explode_bomb();
}
return result;
}
Read six numbers, then check whether
v3[i] == v3[i - 1] * (i + 1)
That is, a simple factorial function.
phase_3
int __cdecl phase_3(char *s)
{
int result; // eax
char v2; // bl
int v3; // [esp+Ch] [ebp-Ch] BYREF
char v4; // [esp+13h] [ebp-5h] BYREF
int v5; // [esp+14h] [ebp-4h] BYREF
if ( sscanf(s, "%d %c %d", &v3, &v4, &v5) <= 2 )
explode_bomb();
result = v3;
switch ( v3 )
{
case 0:
v2 = 'q';
if ( v5 != 777 )
explode_bomb();
return result;
case 1:
v2 = 'b';
if ( v5 != 214 )
explode_bomb();
return result;
case 2:
v2 = 'b';
if ( v5 != 755 )
explode_bomb();
return result;
case 3:
v2 = 'k';
if ( v5 != 251 )
explode_bomb();
return result;
case 4:
v2 = 'o';
if ( v5 != 160 )
explode_bomb();
return result;
case 5:
v2 = 't';
if ( v5 != 458 )
explode_bomb();
return result;
case 6:
v2 = 'v';
if ( v5 != 780 )
explode_bomb();
return result;
case 7:
v2 = 'b';
if ( v5 != 524 )
explode_bomb();
return result;
default:
explode_bomb();
}
if ( v2 != v4 )
explode_bomb();
return result;
}
There are 8 options to choose from, and any choice will successfully defuse.
(Tip: If your v2 shows as a number, you can right-click the number or press r to convert it to an ASCII character.)
For example, in case 0, the three conditions are:
v3 == 0v2 == v4v5 == 777
So the correct input is:
0 q 777
The remaining cases follow the same principle.
phase_4
int __cdecl func4(int a1)
{
int v1; // esi
if ( a1 <= 1 )
return 1;
v1 = func4(a1 - 1);
return v1 + func4(a1 - 2);
}
int __cdecl phase_4(char *s)
{
int result; // eax
int v2; // [esp+14h] [ebp-4h] BYREF
if ( sscanf(s, "%d", &v2) != 1 || v2 <= 0 )
explode_bomb();
result = func4(v2);
if ( result != 55 )
explode_bomb();
return result;
}
Anyone who has studied a bit of recursion will recognize that func4 implements the computation of the nth term of the Fibonacci-like sequence (called here the “rabbit sequence”). But since it's written with naive recursion, its efficiency is extremely poor, with exponential time complexity.
The sequence defined here is:
1 2 3 5 8 13 21 34 55 89 144 ...
Therefore, the correct answer is 9.
In the provided instructions, there's also the following hint:
Phases get progressively harder. There is also a "secret phase" that
only appears if students append a certain string to the solution to
Phase 4.
Next, we open the phase_defused function:
void phase_defused()
{
char v0; // [esp+14h] [ebp-54h] BYREF
char v1[80]; // [esp+18h] [ebp-50h] BYREF
if ( num_input_strings == 6 )
{
if ( sscanf(s, "%d %s", &v0, v1) == 2 && !strings_not_equal(v1, "austinpowers") )
{
printf("Curses, you've found the secret phase!\n");
printf("But finding it and solving it are quite different...\n");
secret_phase();
}
printf("Congratulations! You've defused the bomb!\n");
}
}
Therefore, we need to append the string austinpowers right after the answer 9.
Only when num_input_strings == 6 (meaning all six phases are correctly solved) will the hidden phase be revealed.
phase_5
int __cdecl phase_5(_BYTE *a1)
{
int i; // edx
int result; // eax
char v3[8]; // [esp+10h] [ebp-8h] BYREF
if ( string_length(a1) != 6 )
explode_bomb();
for ( i = 0; i <= 5; ++i )
v3[i] = array_123[a1[i] & 0xF];
v3[6] = 0;
result = strings_not_equal(v3, "giants");
if ( result )
explode_bomb();
return result;
}
The challenge is starting to get a bit more difficult—roughly on par with the second reverse-engineering problem in a freshman competition.
Here's what's happening:
- The program takes the input string and applies a bitwise AND with 15 on each byte (effectively
mod 16). - These values are then used as indices into the
array_123dictionary. - The generated result is compared against the string
giants.
When examining array_123, you'll notice it contains a set of ASCII characters. That means the target string is encoded through this mapping.
To solve it, you can simply write a script to backtrack the values of a1, by determining which input characters map to the corresponding letters in giants.

#include <bits/stdc++.h>
using namespace std;
unsigned char array_123[] =
{
0x69, 0x73, 0x72, 0x76, 0x65, 0x61, 0x77, 0x68, 0x6F, 0x62,
0x70, 0x6E, 0x75, 0x74, 0x66, 0x67
};
char s[]="giants";
int sol[10];
int main(){
for(int i=0;i<6;i++)
{
for(int j=0;j<16;j++)
if(array_123[j]==s[i])
{
sol[i]=j;
break;
}
}
for(int i=0;i<6;i++)
printf("%d ",sol[i]);
return 0;
}
The output result is:
15 0 5 11 13 1
However, the problem requires us to input a string. Since characters with values less than 16 are invisible, we need to add multiples of 16 to make them printable.
Here, I chose to add 96, and the final answer is:
o`ekma
phase_6
int __cdecl phase_6(char *s)
{
int i; // edi
int j; // ebx
int k; // edi
_DWORD *v4; // esi
int l; // ebx
int *v6; // esi
int m; // edi
int *v8; // eax
int *v9; // esi
int n; // edi
int result; // eax
int *v12; // [esp+24h] [ebp-34h]
int v13[6]; // [esp+28h] [ebp-30h]
int input[6]; // [esp+40h] [ebp-18h] BYREF
read_six_numbers(s, (int)input);
for ( i = 0; i <= 5; ++i )
{
if ( (unsigned int)(input[i] - 1) > 5 )
explode_bomb();
for ( j = i + 1; j <= 5; ++j )
{
if ( input[i] == input[j] )
explode_bomb();
}
}
for ( k = 0; k <= 5; ++k )
{
v4 = &node1;
for ( l = 1; l < input[k]; ++l )
v4 = (_DWORD *)v4[2];
v13[k] = (int)v4;
}
v6 = (int *)v13[0];
v12 = (int *)v13[0];
for ( m = 1; m <= 5; ++m )
{
v8 = (int *)v13[m];
v6[2] = (int)v8;
v6 = v8;
}
v8[2] = 0;
v9 = v12;
for ( n = 0; n <= 4; ++n )
{
result = *v9;
if ( *v9 < *(_DWORD *)v9[2] )
explode_bomb();
v9 = (int *)v9[2];
}
return result;
}
This one is rather troublesome, as it involves linked list manipulation and modification, with fairly heavy use of pointers, and the readability of the code and data isn't great.
The general idea is:
- Input a permutation of numbers 1–6.
- Use this permutation to reorder the
nodestructures. - Rebuild a structure called
v13. - Traverse
v13usingv9to check whether the keys inside are in descending order.
Inspecting the address of node1, we find a bunch of raw data (IDA still isn't advanced enough to automatically recognize this structure).
From the problem description file, we know:
Each bomb phase tests a different aspect of machine language programs:
Phase 1: string comparison
Phase 2: loops
Phase 3: conditionals/switches
Phase 4: recursive calls and the stack discipline
Phase 5: pointers
Phase 6: linked lists/pointers/structs
This strongly suggests that the node structure is indeed a linked list. By processing that raw data and converting it into integers, we can reconstruct the node values.
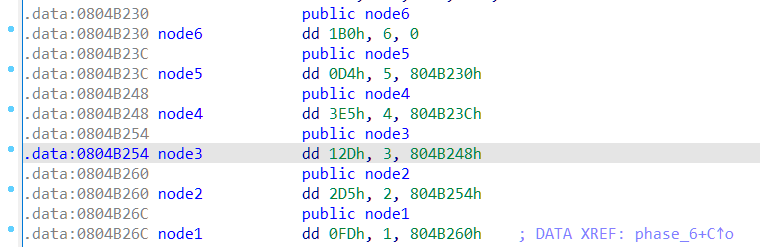
The first value of node is the key, the second is the position in the linked list, and the third corresponds to the next pointer array. This confirms that it's a linked list structure.
Sorting the keys in descending order gives the sequence:
4 2 6 3 1 5
Of course, if you didn't fully understand the structure, you could also solve this by brute force. (The problem statement mentioned: “Each incorrect attempt deducts 0.5 points from your total score.” But since we're solving offline, brute force is still fine!)
Here is the brute-force script, for those interested:
from pwn import *
import itertools
num = ['1','2','3','4','5','6']
for num in itertools.permutations(num,6):
io = process('./bomb')
io.sendline('Public speaking is very easy.')
io.sendline('1 2 6 24 120 720')
io.sendline('0 q 777')
io.sendline('9')
io.sendline('o`ekma')
a = ' '.join(num)
print(a)
io.sendline(a)
for i in range(10):
s = io.recvline()
print(s)
io.close()
# Correct permutation: 4 2 6 3 1 5
secret_phase
int __cdecl fun7(_DWORD *a1, int a2)
{
if ( !a1 )
return -1;
if ( a2 < *a1 )
return 2 * fun7((_DWORD *)a1[1], a2);
if ( a2 == *a1 )
return 0;
return 2 * fun7((_DWORD *)a1[2], a2) + 1;
}
void secret_phase()
{
const char *v0; // eax
int v1; // ebx
v0 = (const char *)read_line();
v1 = __strtol_internal(v0, 0, 10, 0);
if ( (unsigned int)(v1 - 1) > 0x3E8 )
explode_bomb();
if ( fun7(n1, v1) != 7 )
explode_bomb();
printf("Wow! You've defused the secret stage!\n");
phase_defused();
}
Unfortunately, the n1 in the code again appears as raw data, so we have to manually decode it.
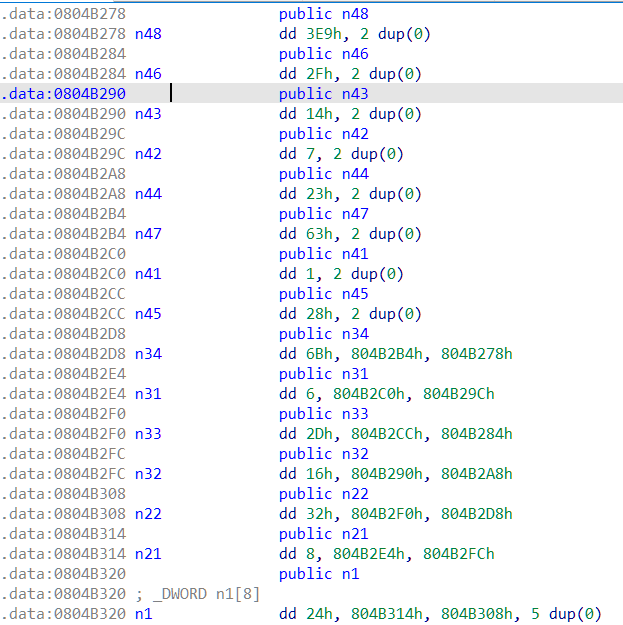
Anyone with some background in data structures can quickly recognize that this looks like a binary tree. If you sketch it out, you'll notice it's actually a Binary Search Tree (BST).
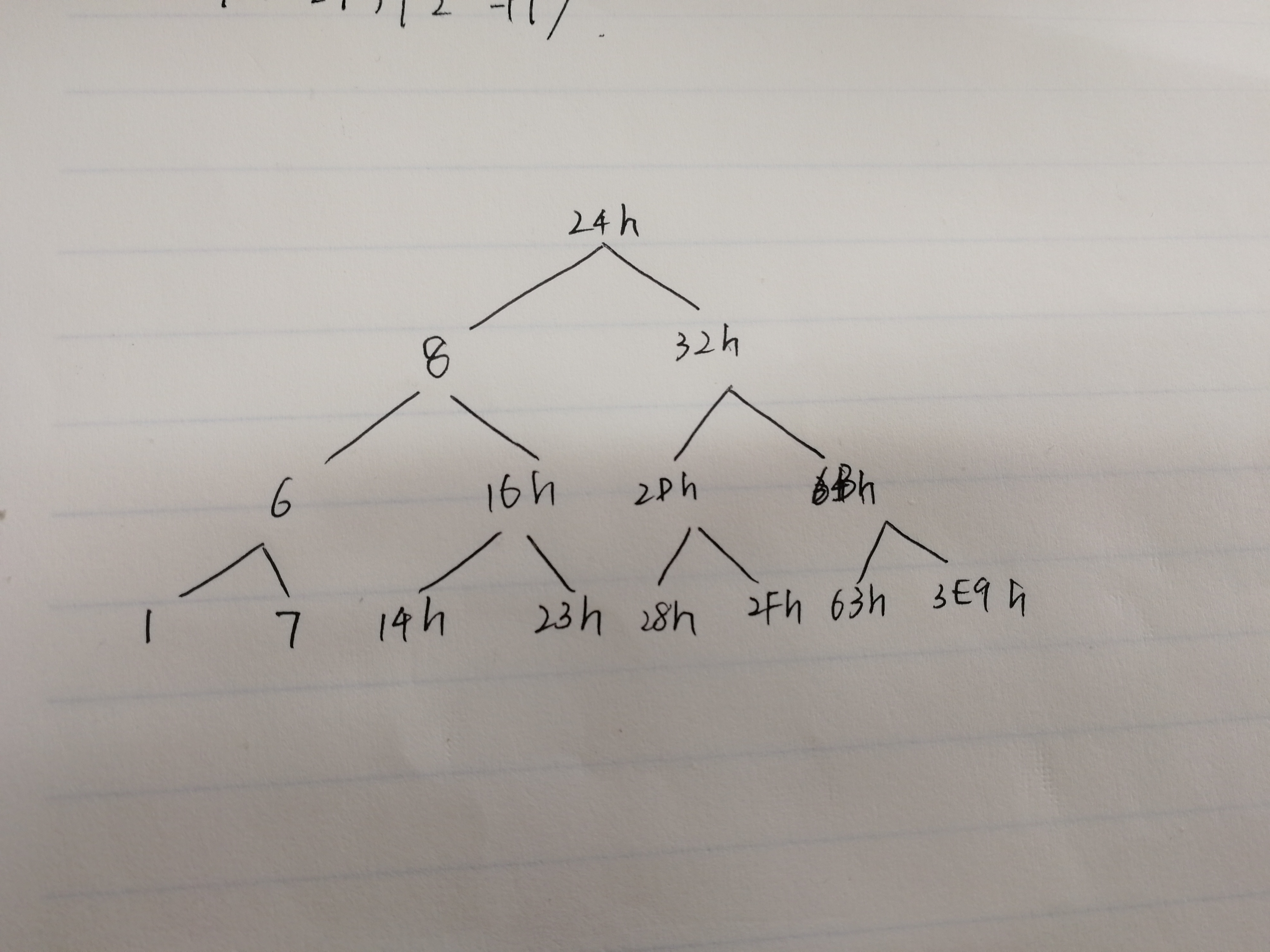
The value I overwrote by hand is 6Bh.
The logic of fun7 is as follows:
- If you backtrack from the right subtree, the value is
val × 2 + 1. - If you backtrack from the left subtree, the value is
val × 2. - Any leaf node has the value
0.
By manually tracing the calculation, you can determine that only the rightmost bottom node, which has the value 3E9h (i.e., 1001), will yield a final root value of 7.
Summary
Lab 3 was indeed easier than Lab 2 (I finished the secret_phase from the evening of the 10th at 9 p.m. to the morning of the 11th at 9:30 a.m.), but it was not as simple as I initially imagined—certainly not something you can just solve by casually opening IDA.
I would recommend that next year's students must complete Lab 1 (decoding lab) and Lab 3 (binary bomb) for the security project, and treat Lab 2 (buffer bomb) as optional. Lab 2 requires too much prerequisite knowledge, which most students cannot handle. The fragmented hints scattered throughout the semester inevitably affect a systematic study of the stack later on.