注意:本文仅对微信拼手气红包的算法进行分析,指出最佳的抢红包位置,并不能帮助读者从微信红包中盈利。
背景
春节期间,我与家人共4人组建了一个红包群,约定每天中午饭后和晚上黄金时间开展抢红包活动,规则如下:
- 发出一个总面值200元,份数为4的拼手气红包。
- 手气最佳者,接着发下一个红包。
- 每轮进行20分钟,最后一个手气最佳者发明天的第一个红包。(第一天的第一个红包由群主发)
然后由于我的手速较快,每次几乎总能抢到第一个。于是在某一天,我连续五次手气最佳,在那轮不出意外地输掉了800+。于是我第二天改变了策略,等红包出来后5秒钟再抢,这一天两轮我都赢了200+——看来我的策略是正确的,我每天的输赢确实跟抢红包的位置有一定的关系。
于是,有一点编程基础的我,决定用计算机模拟一下抢红包的过程,计算一下当抢红包次数足够多的情况下:
- 每个位置手气最佳的概率。
- 每个位置输赢的期望。
实现
拼手气红包算法
经上网查阅,微信的拼手气红包金额分配是这样实现的。
我们假设总金额为,抢红包人数为,那么:
第一个红包金额的范围是
第二个红包金额的范围是
第三个红包金额的范围是
......
倒数第二个红包和最后一个红包的范围都是
其中在以上范围内均匀随机。
由此可见,后面的红包都是基于前面抢过红包的金额之和来进行即时计算的,这样做不需要预处理红包内部的金额。这对于微信这种容纳数十亿人的交流平台,节省了一大笔时间与空间的开销。
当然,这样做的后果就是:虽然在哪个位置,抢到红包的金额的数学期望是相等的(然而我并不会证),但是每个位置可能的金额的方差却不相同。一般来说,可能金额的方差随着次序的靠后而逐渐增大(这就是为什么大红包大多都出在后面的原因)。
我在查阅微信算法之前,自己也构思了一个需要预处理的金额分配算法,思路如下:
我们假设总金额为,抢红包人数为,那么:
想象一条长为的线段,在这上面随机取个点,我们将其从左到右命名为~.
于是分配到的金额为:
,且
编者认为,这种做法可以保证人人公平。
编写代码与测试
根据以上思想,我编写了如下c++代码。
(为什么不用python?因为python生成个随机数太慢了)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
| #include <iostream>
#include <random>
#include <ctime>
#include <algorithm>
#define PERSON_MAX 100
#define INI_BALANCE 0
int NUM_PERSON;
#define NUM_ENV 200
int ITER_NUM;
int MODE;
using namespace std;
double balance[PERSON_MAX], money[PERSON_MAX];
int num_first[PERSON_MAX];
default_random_engine f(time(NULL));
uniform_real_distribution<double> rnd(0, 1);
void init() {
cout << "请输入抢红包的人数(小于100)" << endl;
cin >> NUM_PERSON;
cout << "请输入发红包的次数(小于一百万)" << endl;
cin >> ITER_NUM;
cout << "请输入红包生成规则:1.微信规则,2.我的规则" << endl;
cin >> MODE;
for(int i = 0; i < NUM_PERSON; i++) {
balance[i] = INI_BALANCE;
}
}
void rand1() {
double money_left = NUM_ENV;
for(int i = 0; i < NUM_PERSON - 1; i++) {
money[i] = rnd(f) * money_left / (NUM_PERSON - i) * 2;
money_left -= money[i];
}
money[NUM_PERSON - 1] = money_left;
}
double pin[PERSON_MAX];
void rand2() {
for(int i = 0; i < NUM_PERSON - 1; i++) {
pin[i] = rnd(f) * NUM_ENV;
}
sort(pin, pin + NUM_PERSON - 1);
money[0] = pin[0];
for(int i = 1; i < NUM_PERSON - 1; i++) {
money[i] = pin[i] - pin[i - 1];
}
money[NUM_PERSON - 1] = NUM_ENV - pin[NUM_PERSON - 2];
}
int gen(int who_first, int mode) {
balance[who_first] -= NUM_ENV;
if(mode == 1) rand1();
else rand2();
double max_money = -1.0;
for(int i = 0; i < NUM_PERSON; i++) {
balance[i] += money[i];
if(money[i] > max_money) {
max_money = money[i];
who_first = i;
}
}
num_first[who_first]++;
return who_first;
}
void out() {
printf("经过%d次抢红包后,总是抢第i个红包的人手气最佳的概率:\n", ITER_NUM);
for(int i = 0; i < NUM_PERSON; i++) {
printf("%lf", 100.0 * num_first[i] / ITER_NUM);
cout<<"% ";
}
printf("\n\n");
printf("经过%d次抢红包后,总是抢第i个红包的人的每次抢红包的输赢期望:\n", ITER_NUM);
for(int i = 0; i < NUM_PERSON; i++) {
printf("%lf ", balance[i] / ITER_NUM);
}
}
int main()
{
init();
int who_first = 0;
for(int i = 0; i < ITER_NUM; i++) {
who_first = gen(who_first, MODE);
}
out();
return 0;
}
|
首先,我针对我们家的情况进行的实验,结果如下:
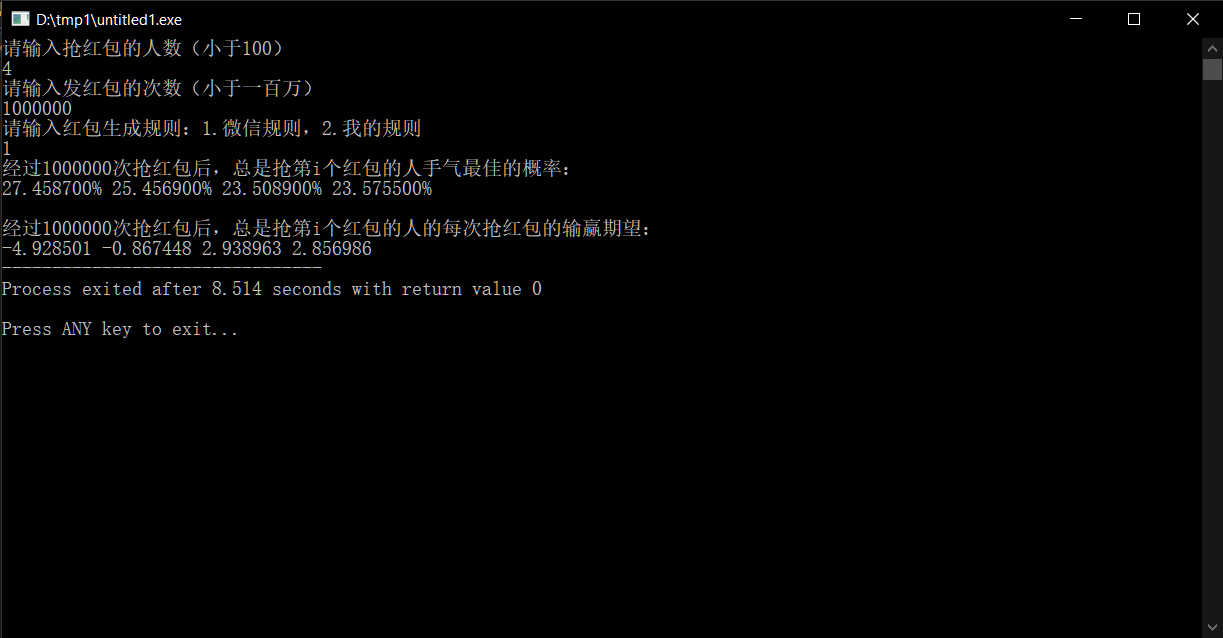
由此可见,最先抢红包的人有约27.4%的概率手气最佳,这一数据比最后两位高出了大约3.9%。别看这个数字很小,可20分钟至少也能发30个红包,也能积攒出一个红包200元的差距了。
再来看期望,最先抢红包的人平均每一局将近输掉了5元,再乘上一轮红包雨的红包数量,大概是150~200元之间,跟算概率的结果相仿。
而最后两个抢红包的,无论是从手气最佳的概率上,还是从赢钱的期望上,都是最低(佳)的,而且地位相同。
拓展思考
增加人数
那么,如果抢红包的人数不是4人,而是一个大家族(比如说20人),又会怎么样呢?
结果出乎我的意料。
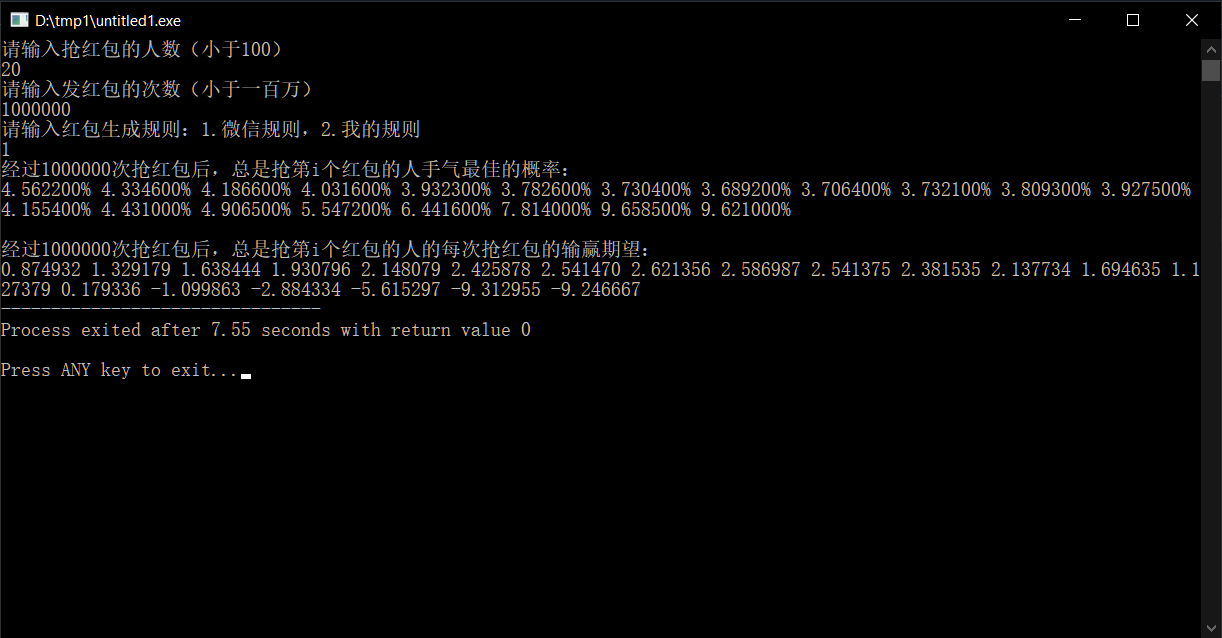
我们可以看到,手气最佳的概率先是从第一个抢红包的4.65%,下降到第8个的3.69%,然后又迅速上升至最后两位的9.64%(均值),是平均值5%的几乎两倍。
同时赢钱期望也是先增后减,只不过到最后5个人才开始输钱。
即使是100个人抢红包,最后两个人手气最佳的概率也有8%,而且输钱的期望增加到了14元。
改进规则
那么,如果是抢的最少的人发红包,又会怎么样呢?
对于人数较少的时候,先抢红包的人不容易手气最差,而且赢得比之前的4号更多,这符合我们的直觉。
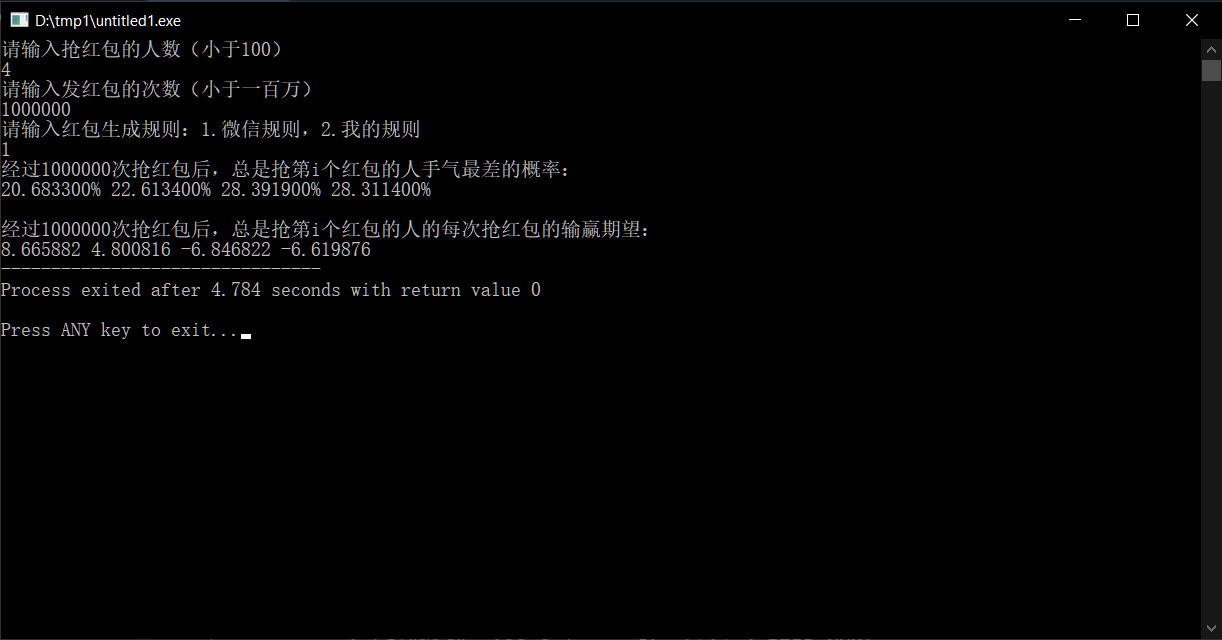
对于人数较多的时候,手气最差的增减性与输赢的期望与人数较少的情况一致,只不过最后两位输得比之前的~少了许多。
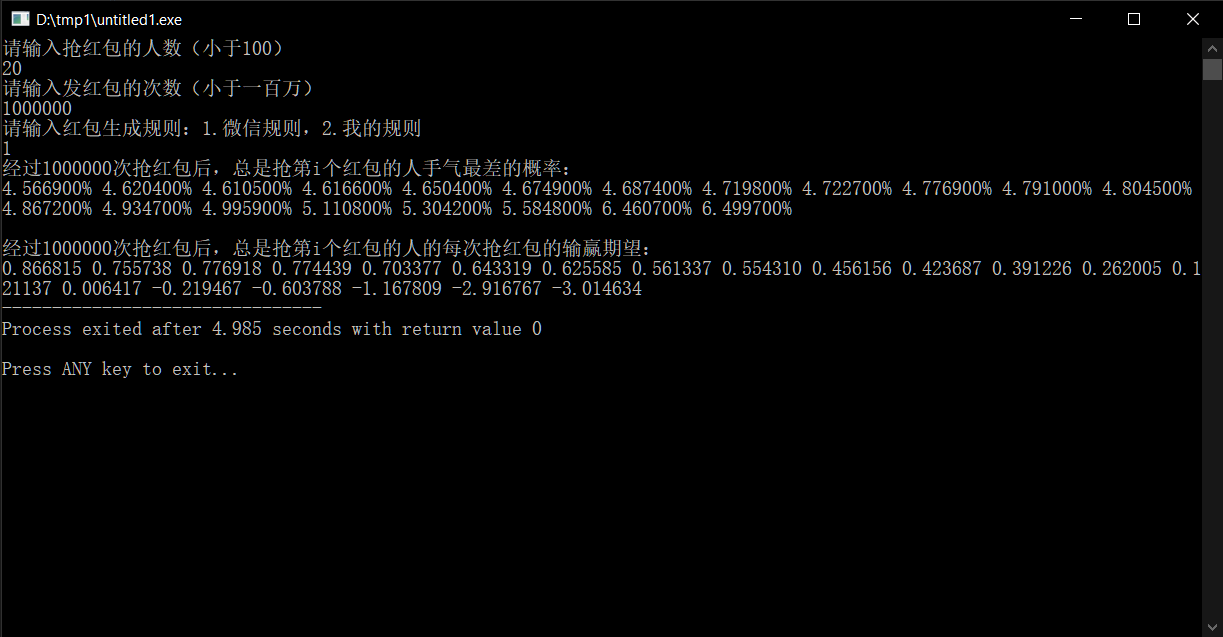
调整算法
最后,我们来看看我的算法究竟是否公平。
这是人数较少的情况:
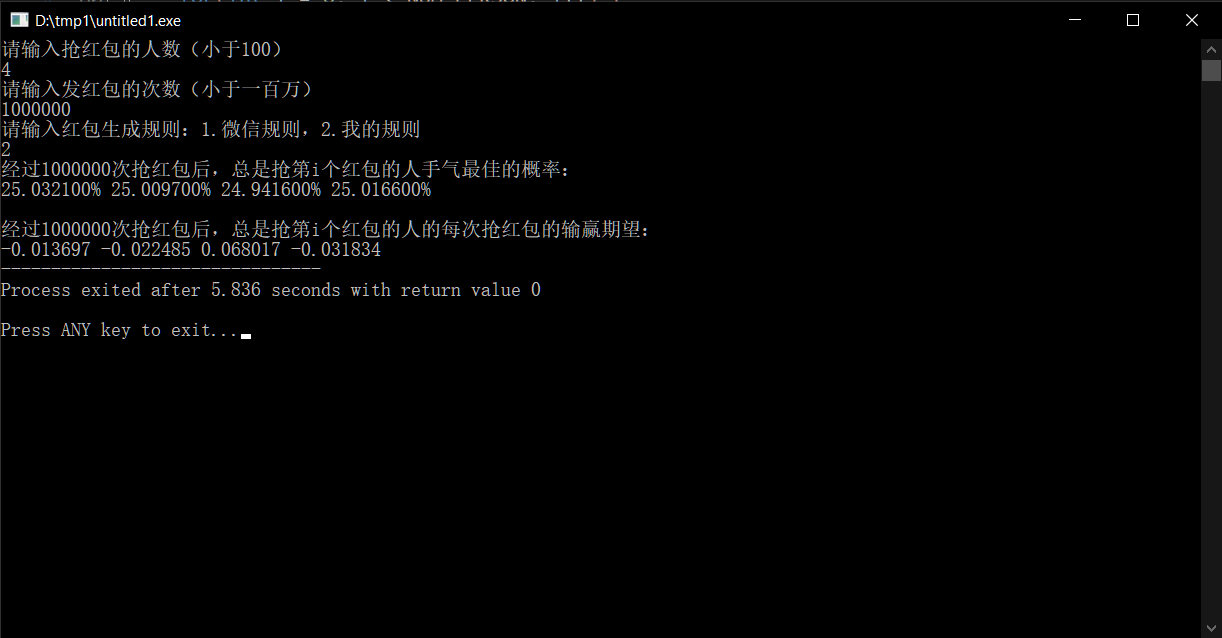
这是人数较多的情况:
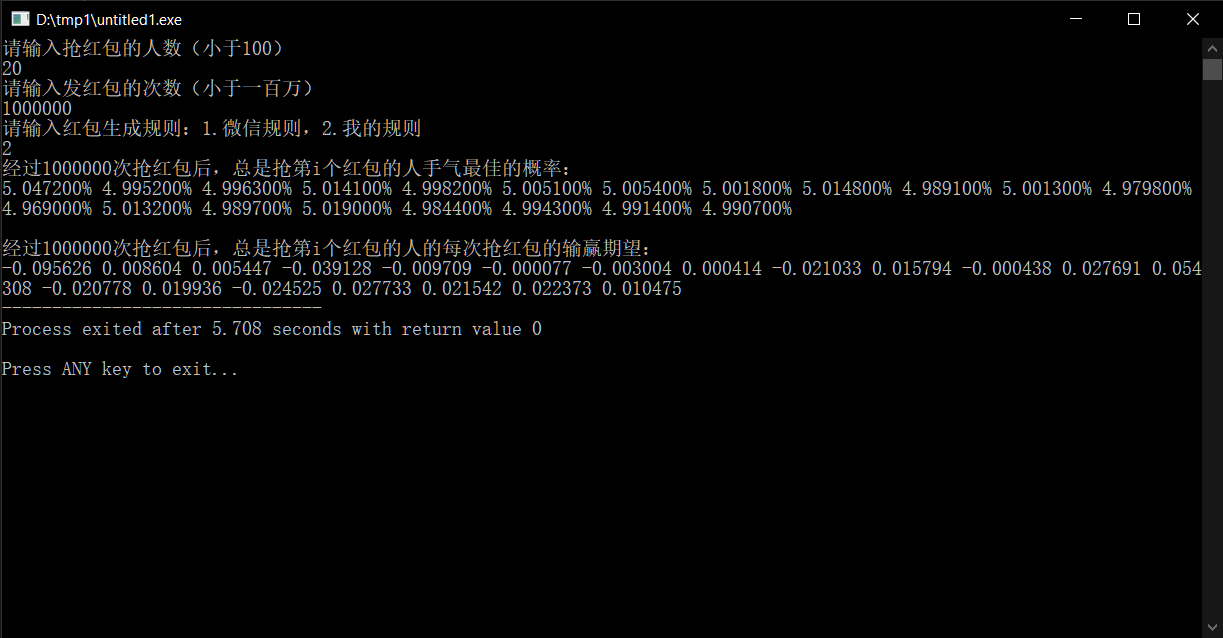
由此可见,每轮红包的输赢期望稳定在了几分钱以内,可以说是做到了基本公平。
后记
程序编写好后,我把结论分享给了父母,于是父亲在当天午后的抢红包活动中始终赖到最后一位,而我只能则随机在前三位游走,无可奈何。
最后,父亲赚了249元,而我输了253元。看来算清楚赢钱的套路并不能帮助我赢钱啊qwq。





