《加密与解密》学习笔记
与csapp相比,《加密与解密》更偏向于实践一点,内容丰富但比较杂。汇编代码语法与csapp不同,采用intel语法。
基础知识
诸如API、Unicode、Little-endian之类的介绍,此处略去。
(但是Win32 API和WOW64放到这一段就很劝退,算了还是将来用到再查文档吧——)
动态分析技术
OllyDbg
(学了硬件断点、消息断点、条件断点、内存断点,还有trace功能)
x64dbg
MDebugWinDbg
静态分析技术
PEiD/ExeinfoPE
ODDisasm、BeaEngine、Udis86、Capstone、AsmJit、KeystoneIDA yyds!
(IDA提供了一项我以前并不知道的功能,就是在系统API处按下F1键会弹出该API的用法,然而这个功能只支持.hlp文件,所以它并没有什么用)
WinHex/010editor
逆向分析技术
32位软件逆向技术
启动函数
WinAPI集中区域,看不懂直接跳。
函数
第N次复习栈调用的机会。
常见的调用约定(VARARG指参数的个数不确定):

①:仅当平衡栈者为caller时适用。
数据结构
局部变量:使用栈存放。
全局变量:.data区段 / cs:xxxx
数组:基址加变址寻址。为了看懂数组的汇编代码,狂补csapp的相应章节。
虚函数——1/15/2022
引用虚函数:先用指针(通常由new或malloc分配)指向虚函数表(VTBL),该表存放着所有虚函数的地址,再使用虚函数表指针(VPTR)调用函数。
根据虚表可以还原这个类的虚函数个数,及虚函数代码。
疑问:汇编代码中0040101B地址,为什么
eax=*VTBL=**Add(),而不是eax=*VTBL=&Add()?
控制语句——1/17/2022
(大多数都在csapp讲过了,没什么特别重要的点)
a & (-b)且b是2的幂,等价于
sbb A B指令:A = A - B - CF
循环语句——1/23/2022
与csapp的讲述相同,本质就是高地址向低地址的跳转。
更正:
两个方案的
i < 5应改为i <= 5。未优化代码中0x40102E处的注释应是“由高地址向低地址区域”。
数学运算符——1/23/2022
加减法使用lea指令加速运算。
乘法使用位移指令加速。
除法在除数已知的情况下会乘一个常数(类似于逆元),取结果的高位。特别的,如果除数是2的幂,那么直接右移即可。
如果结果是负数,值会+1(可能与负数的向0舍入有关)。
文本字符串——1/23/2022
目前惯用的C字符串结尾为'\0'。其余字符串为DOS字符串(结尾为$)、PASCAL字符串(单字节开头的ANSI字符表示长度)和Delphi字符串(双字节或四字节)。
如果出现mov ecx, FFFFFFFF一句,代表程序很有可能获取字符串的长度,汇编代码如下。

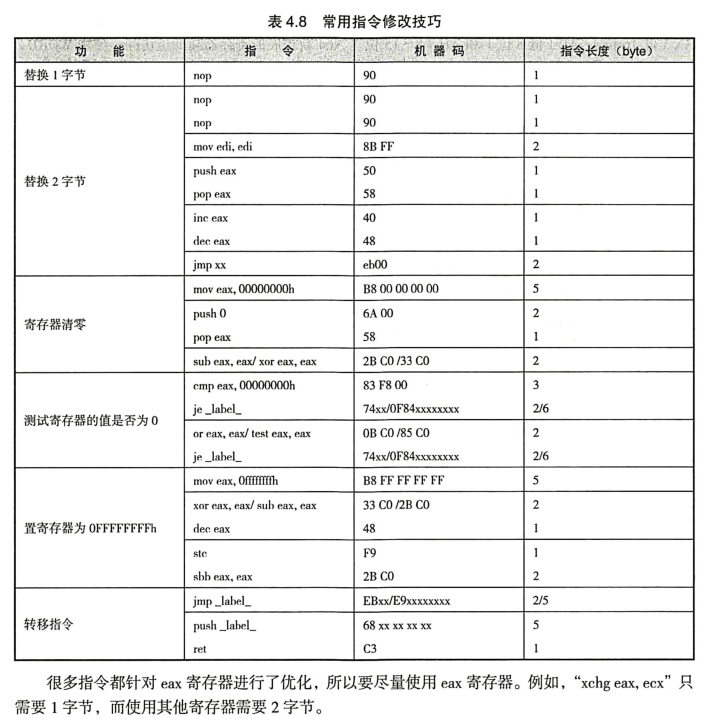
指令修改技巧——1/24/2022
感觉没什么好说的,直接贴图总结吧。
64位软件逆向技术——1/24/2022
寄存器~循环语句
- 调用约定只有一种,规则如下(又跟csapp不一样可还行):
- 前四个参数用寄存器,剩下入栈。
- 寄存器使用顺序为rcx、rdx、r8、r9(浮点为xmm0~xmm3)
- 入栈参数顺序:从右到左。
- 栈会为这四个参数预留32 byte的占空间,即使只传入了2个参数。
- rep指令:重复后一个参数的指令,同时ecx--,直到ecx--之后值为0结束。(因此当ecx为0时会执行
次) - stos指令:将eax中的数据放入edi所指的内存地址中,同时edi+=4 byte。常与rep指令连用,用来将栈空间填充为0xcccccccc(烫烫烫)。
- movsb指令:将数据从 esi 指向的内存位置复制到 edi 指向的内存位置,同时这两个寄存器自动+=1 byte(因为后缀为'b')。常与rep指令连用,用来复制拷贝数组、结构体等。
- 对于结构体传参,若结构体大小 <= 8 byte,那么直接使用寄存器传参。如果大于就传入结构体的地址,通过偏移来访问结构体内容。
- 类的成员调用传参会比普通函数多一个this指针。 >什么是__security_check_cookie? > >通过在栈中未使用的空间中填入0xcc,并将该值与rsp指针异或,得到的值就是__security_check_cookie。因为现在的程序开启了栈随机化的保护,使得cookie的值无法被预测,因此是一种有效防止栈溢出的方式。
这句话是什么意思?(P150)
mov eax, ds:(jpt_140001060 - 140000000h)[rcx+rax*4]类似于
(a)[b+c*d]的操作类似于AT&T语法中的a(b,c,d),就是b+c*d+a的意思。这里实现了一个进入跳表的操作,为switch语句的分支跳转做准备。
- switch语句的优化除了跳表,还有判定树优化。
- 64位的call指令机器码为
FF 15 xx xx xx xx,其中后四个byte为相对偏移,而不是内存地址。
数学运算符
除法的各种优化技巧
对于除数为
的情况,公式为 x >> n(被除数为正),和(x + 2**n - 1) >> n(被除数为负).对于除数为
的情况,与上述相同,只需结果取反即可。 对于除数不为
的情况,有两种优化方式,这里以64位为例。 其一是
x * c >> 64 >> n(被除数为正),和(x * c >> 64 >> n) + 1(被除数为负)。其中c为正数,n可能为0。其二是
(x * c >> 64) + x >> n(被除数为正),和((x * c >> 64) + x >> n) + 1(被除数为负)。其中c为负数。除数可以用
计算,其中 为magic_num。
对于公式二的略证(设
为除数): 由于溢出,
,即化归为公式一的情况,以下过程略。 Q:为什么要+x?
因为+x相当于
加上 。之前 是 0x92492493,转成signed后是0x92492493-0x100000000,再加上就是它本身了。如果不加这个x,得到的就是一个负数。 对于除数不为
的情况,公式与上述基本相同,只是第一个公式c为负数;第二个公式c为正数,且中间的“+”应改为“-”。其中, , 为magic_num。 无符号除法时,对于除数为
的情况,公式为 x >> n.无符号除法时,对于除数不为
,公式有两种: 其一是
x * c >> 64 >> n,其中。 其二是
(x - (x * c >> 64) >> n1) + (x * c >> 64) >> n2,其中,, 为magic_num。
对于公式二的略证(设
为除数): 这辈子都不可能证的。所以,书上公式二给出的
是错误的,它仅仅符合 的情况。下方的链接也说明我的公式的正确性。 https://zneak.github.io/fcd/2017/02/19/divisions.html
取模的一点优化技巧
声明:在C语言中,取模结果的符号与被除数符号相同,而且其值与两个参数都为正数的结果相同,这一点与python有所区别。
如分别计算
5 % 3、(-5) % 3、5 % (-3)、(-5) % (-3)的值,C得到的结果是2 -2 2 -2,而python则是2 1 -1 -2.除数为
的情况,有两种优化方式: 其一是
x & ((1 << n) - 1)(当被除数为正时)和((x & ((1 << n) - 1)) - 1 | (~ ((1 << n) - 1))) + 1(当被除数为负时)。在这里,先减一后加一是为了处理余数为0的特殊情况。当被除数为负时,还有一种优化公式为
((x + ((1 << n) - 1)) & ((1 << n) - 1)) - ((1 << n) - 1)。(经编者测试,编译器基本都是使用了这个公式进行优化)
对于两个公式的合理性说明:
公式一:
C处理负数取模跟处理正数取模恰好相反,直接在前
位全部置为1即可。 因此
| (~ ((1 << n) - 1))就是做的这件事。其实前面那个
& (~ ((1 << n) - 1))完全可以舍去,但是为了减少判断,就与正数的情况统一了。当
的后 位为 时,如果仍按照负数处理,在前 位全部置为 ,那么得到的结果就是 . 通过减
,将 的后 位都置为 ,之后前 位置为 后再加一,答案就是 了。 一般地,设你开始减掉了
,那么最后模的范围就是 ~ . 公式二:
以
为例: 
观察可知,当
x < 0时,第二行中的第列元素,是第三行中第 列元素减 的值,故由此推广可得出上述公式。 - 除数不为
的情况时,优化方式为 x - x / c * c,其中为除数。
虚函数
对析构函数虚拟化,在编译器中会生成一个普通析构函数,和在虚表里带delete的析构函数。
为了防止虚析构函数对空间重复释放,VC++的做法是给析构函数增加一个参数(参数为1就释放),而gcc的做法是在虚表里放两个析构函数的地址。
单个对象的内存布局:
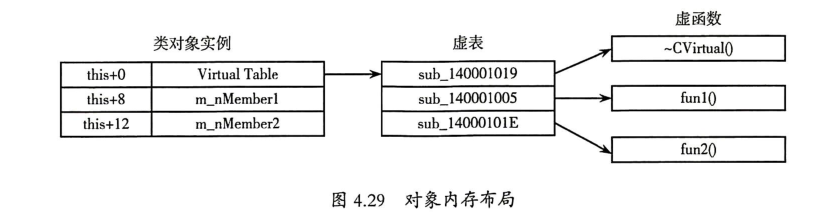
构造函数的调用顺序(可作为还原类继承层次的一个依据):
- 调用虚基类构造函数(多个按继承顺序调用)。
- 调用普通基类构造函数(多个按继承顺序调用)。
- 调用对象成员的构造函数(多个按定义顺序调用)。
- 调用派生构造函数。
析构函数的调用顺序则反之。
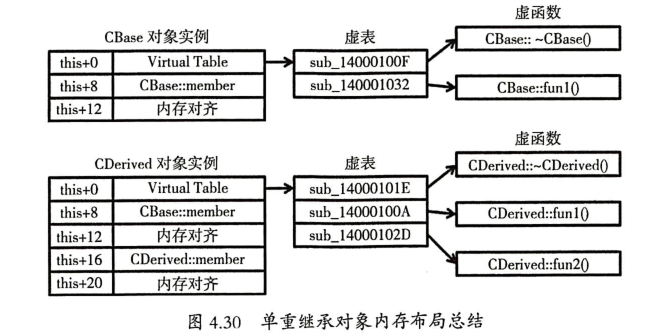
派生类的虚表填充过程(可作为还原类继承层次的一个依据):
- 复制基类的虚表。
- 如果派生类虚函数有覆盖基类的虚函数,使用派生类的虚函数地址覆盖对应表项。
- 如果派生类有新增的虚函数,将其放在虚表后面。
单重继承对象内存布局:
多重继承的特点是构造函数会有两次构造初始化虚表的操作。
多重继承对象内存布局:
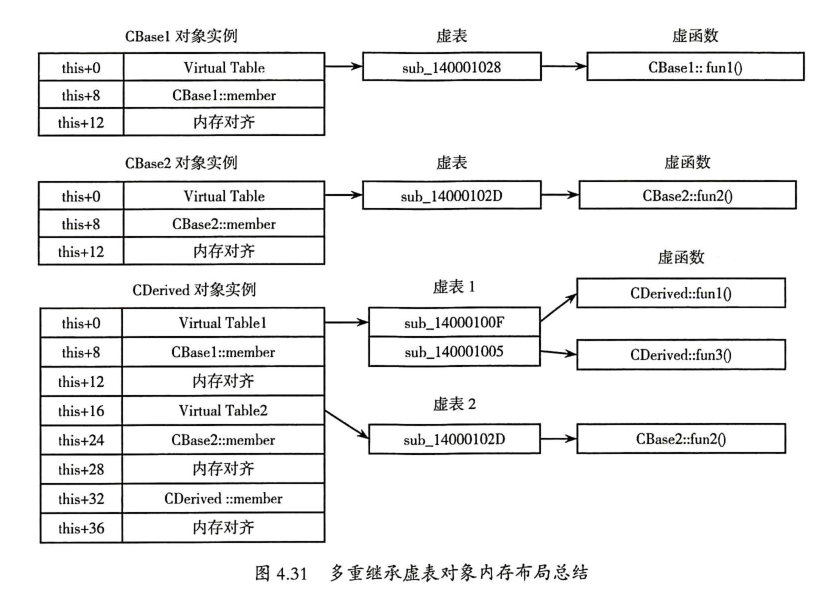
菱形继承为了防止base类的内存冗余,会使用虚继承(virtual public: <class name>)。具体实现方式是在构造函数中多传入一个参数,用来表示是否调用虚基类的构造。
为了方便定位虚基类在对象内存中的位置,做了一个8字节的虚基类偏移表(位于全局数据区),后4字节表示虚基类在当前虚基类偏移表中的偏移。
判定虚继承的另一种方式是构造函数是否有初始化虚基类偏移表的操作。
菱形继承对象内存布局
(内心逐渐崩溃):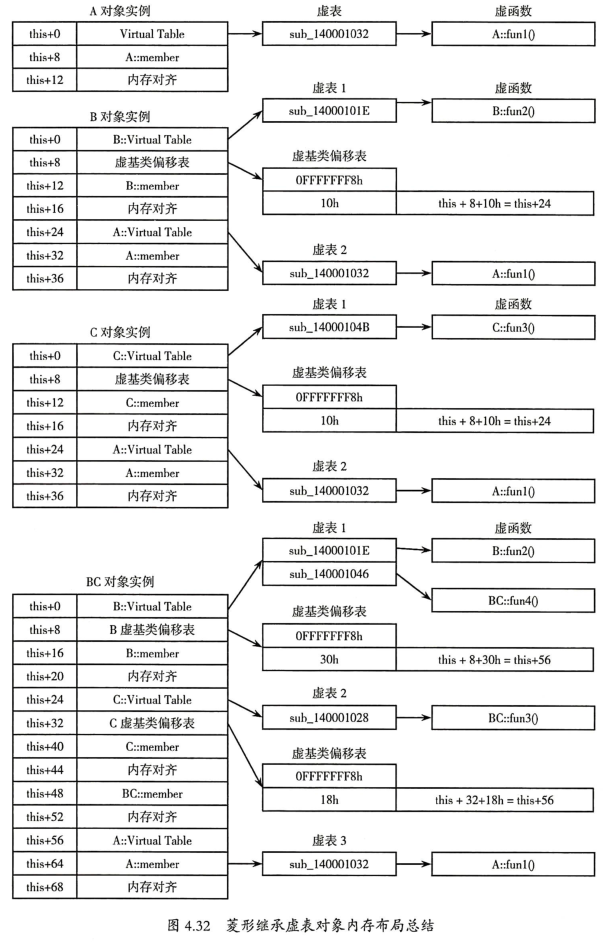
在IDA中,
vftable表示虚表,而vbtable表示虚基类偏移表。甚至IDA可以自动指出某个vftable/vbtable地址指向了哪一个类,还是很智能的。父类为抽象类虚表与单重继承的唯一区别是, 父类的虚表代码为
_purecall,其功能是显示错误信息并退出程序。如果发现某个类有_purecall虚表项,就可以怀疑它是抽象类。
演示版保护技术
序列号保护方式——2/4/2022
- 读入注册码的API:
GetWindowText,GetDlgItemText,GetDlgItemInt等。 - 显示注册码正误的API:
MessageBox,MessageBoxEx,ShowWindow,CreateDialogParam,DialogBoxParam等。 - 对于使用明文比较注册码的保护方式,可以在Ollydbg中打开内存窗口,按Ctrl+B搜索输入的序列号(找到输入的内存地址),多数情况下真正的序列号在该地址±90h字节的地方。
- 可以使用OllyDbg中的Asm2Clipboard插件提取反汇编嵌入C。转换时需注意栈平衡、数据进制、汇编语法格式、字符串引用等。
警告窗口——2/7/2022
- 窗口ID提取:exescope或resource hacker。
DialogBoxParam原型如下:
1 | int DialogBoxParam( |
- 去除警告窗口的两种方式:
- 汇编跳过警告窗口。
- 将警告窗口的参数替换成正常窗口的参数。
时间限制——2/8/2022
- 常见的计时器函数:
SetTimer(),KillTimer(),timeSetEvent(),GetTickCount(),timeGetTime(). - 常见的用于获取时间的函数:
GetSystemTime(),GetLocalTime(),GetFileTime(). - 去除时间限制的两种方式:
- 跳过时间函数。
- 跳过判断超时跳转退出的函数。
- 可以使用变速齿轮辅助调试(尚未成功)。
菜单功能限制——2/9/2022
- 相关函数:
EnableMenuItem()函数为
BOOL EnableMenuItem(HMENU hMenu, UINT uIDEnableItem, UINT uEnable)。其中uEnable项有MF_ENABLED(0h),MF_GRAYED(1h),MF_DISABLED(2h),MF_COMMAND和MF_BYPOSITION.EnableWindow()函数为
BOOL EnableWindow(HWND hWnd, BOOL bEnble)。函数返回非0表示成功,0表示失败。
- 去除限制的方式(只在完整版与试用版文件相同时才可用):修改调用这两个函数push时的
Enable参数。
KeyFile保护——2/10/2022
相关函数:
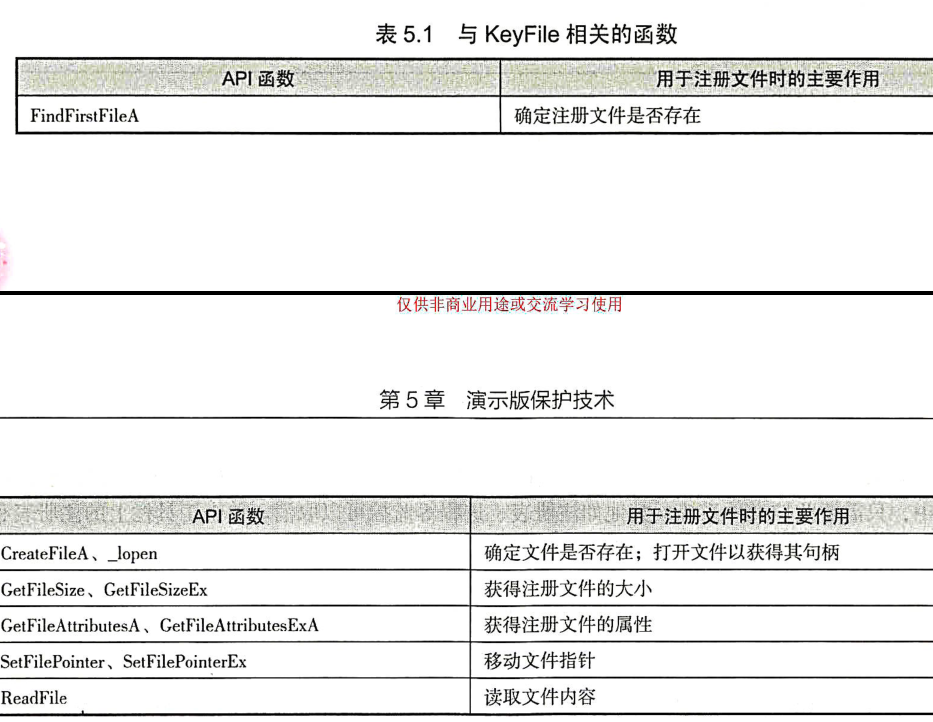
lods指令:
lods byte ptr [esi],将[esi]指向的一字节数据放入eax中,同时esi++。拆解思路:
- 使用Process Monitor监视程序对文件的操作,以找到KeyFile的文件名。
- 用十六进制编辑器编辑KeyFile。
- 在调试器里用CreateFile设断,查看打开的文件名指针,并记下返回句柄。
- 用ReadFile函数设断,分析传递给ReadFile函数的文件句柄和缓冲区地址。文件句柄一般和第3步返回的相同。对缓冲区存放的字节设内存断点,监视读取的KeyFile内容。
网络验证——2/12/2022
相关函数:
send()函数,微软扩展为WSASend()
1
2
3
4
5
6int send(
SOCKET s,
const char FAR *buf,
int len,
int flags
);recv()函数,微软扩展为WSARecv()
1
2
3
4
5
6int recv(
SOCKET s,
char FAR *buf,
int len,
int flags
);拆解思路:
- 分析发送和接收的数据包。(关键)
- 两种方式:
- 编写一个服务端用来接收和发送数据。如果客户端使用域名登录,可以修改hosts文件;如果使用IP直连,可以用
inet_addr或connect设断将IP指向本地,也可以使用代理软件做到这一点。 - 直接修改客户端程序。先将接收的正确数据包粘贴到某个空白地址,然后跳过
send()、recv()函数并替换为处理正确数据包的函数,最后将诸如“连接失败”一类的对话框跳过即可。
- 编写一个服务端用来接收和发送数据。如果客户端使用域名登录,可以修改hosts文件;如果使用IP直连,可以用
疑问:getasm.py脚本似乎不与IDA 7.6相兼容,如何重新实现以下代码?
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
##《加密与解密》第四版
##code by DarkNess0ut
import os
import sys
def Getasm(ea_from, ea_to, range1, range2):
fp = open("code.txt","w")
ea = ea_from
while ea < ea_to:
cmd = GetMnem(ea)
if cmd == "mov" or cmd == "lea":
opcode = Dword(NextNotTail(ea)-4)
if opcode < 0: #opcode < 0,处理 mov edx, [ebp-350]指令,否则处理mov edx, [ebp+350]
opcode = (~opcode + 1)
Message("-> %08X %08X\n" % (ea, opcode))
if range1 <= opcode <= range2:
delta = opcode - range1
MakeComm(ea, "// +0x%04X" % delta) # 加注释到IDA中
fp.write("%08X %s\n" % (ea, GetDisasm(ea)))
ea = NextNotTail(ea)
fp.close()
Message("OK!")
Getasm(0x401000,0x40F951,0x41AE68,0x0041AEC1);
光盘检测——2/11/2022
相关函数:
GetDriveType(),获取磁盘驱动器的类型
1
2
3
4
5
6
7
8
9
10
11
12
13UINT GetDriveType(
LPCTSTR lpRootPathName
);
/*
返回值:
0:驱动器不能识别。
1:根目录不存在。
2:移动储存器。
3:固定驱动器(硬盘)。
4:远程驱动器(网络)。
5:CD-ROM驱动器。
6:RAM disk。
*/GetLogicalDrives(),获取逻辑驱动器符号,无参数
1
2
3
4
5
6
7
8/*
返回值:
如果失败返回0,否则返回由位掩码表示当前可用驱动器,如
bit 0 drive A
bit 1 drive B
bit 2 drive C
......
*/GetLogicalDriveStrings(),即获取逻辑驱动器的根驱动器路径
1
2
3
4
5
6
7
8
9DWORD GetLogicalDriveStrings(
DWORD nBufferLength,
LPTSTR lpBuffer
);
/*
返回值:
如果失败返回0
成功返回实际的字符数
*/GetFileAttributes(),判断指定文件的属性
1
2
3DWORD GetFileAttributes(
LPCTSTR lpFileName
);拆解方式:
- 对于较为简单的光盘检测(先获得所有驱动器列表,再检查每个驱动器的类型,如果是光驱,使用
CreateFile()或FindFirstFile()函数检查文件是否存在,以及属性、大小、内容等),只需利用上述函数设置断点,找到检查光驱的地方,修改判断指令即可。 - 对于增强类型(程序运行的关键数据被放在了光盘中),可以使用刻录工具复制多份,也可以使用虚拟光驱程序模拟正版光盘(其中Daemon
Tools
不仅免费,还能模拟一些加密光盘)。
- 对于较为简单的光盘检测(先获得所有驱动器列表,再检查每个驱动器的类型,如果是光驱,使用
只运行1个实例——2/11/2022
实现方法:
查找窗口法:如果查找到相同窗口类名和标题的窗口,就退出程序。通过
FindWindowA(),GetWindowText()实现。1
2
3
4
5HWND FindWindowA(
LPCTSTR lpClassName,
LPCTSTR lpWindowName
);
//若未找到相符的窗口,则返回0使用互斥对象:一般用
CreateMutexA()实现,作用是创建有名或者无名的互斥对象(什么东西)。1
2
3
4
5
6HANDLE CreateMutexA(
LPSECURITY_ATTRIBUTES lpMutexAttributes, //安全属性
BOOL bInitialOwner, //互斥对象初始身份
LPCTSTR lpName //指向互斥对象名
);
//如果函数调用成功,返回互斥对象句柄使用共享区块(Section)。该区块拥有读取、写入和共享保护属性,可以让多个实例共享同一内存块。将一个变量作为计数器放到该区块中,该应用程序的所有实例可以共享该变量,从而通过该变量得知有没有正在运行的实例。
拆解方式:
- 修改应用程序的窗口标题。
- 修改
FindWindow()等函数的返回值(或者修改判断指令)。
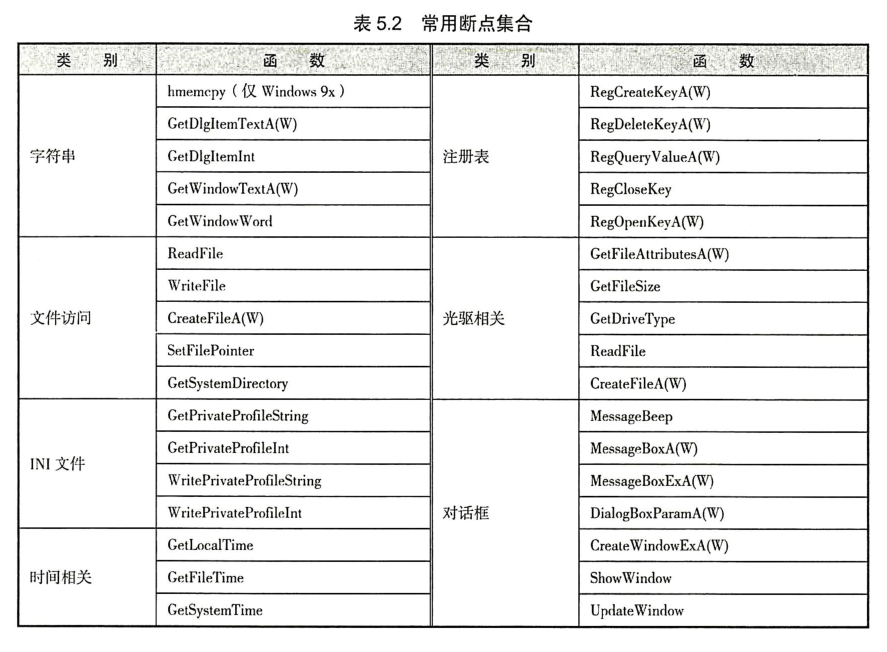
常用断点设置技巧——2/11/2022
掌握Win32编程技巧还是很重要滴!
加密算法
本节笔记的记录主要以算法识别为主,不涉及算法具体过程(公钥除外,因为没有特殊常数),汇编分析与crack操作。
可以使用IDA的FindCrypt或者PEiD的Krypto ANALyzer来辅助分析算法。
单项散列算法——2/27/2022
MD5
重要常数:
初始化消息摘要
67452301h,efcdab89h,98badcfeh,10325476h.floor(2**32 * abs(sin(i)))对应的32位值,如d76aa478h.
可能的变种方式:
- 修改前面的四个常数。
- 修改原串的填充方式。
- 修改hash变换的处理过程。
SHA
SHA-1的常数5a827999h,6ed9eba1h,8f1bbcdch,ca62c1d6h.
SHA-1的160位的初始化消息摘要67452301h,efcdab89h,98badcfeh,10325476h,c3d2e1f0h.
SHA-256、SHA384、SHA512的初始化消息摘要:

SM3
公开的国密算法,过程简述:https://zhuanlan.zhihu.com/p/129692191
可能的代码实现:https://blog.csdn.net/a344288106/article/details/80094878
常数?
79CC4519h,7A879D8Ah初始化消息摘要?
7380166Fh,4914B2B9h,172442D7h,DA8A0600h,A96F30BCh,163138AAh,E38DEE4Dh,B0FB0E4Eh
对称加密算法——2/28/2022
RC4
RC4算法识别:

从网上嫖来的解密脚本:
1 | import base64 |
TEA
常数为0x9e3779b9,来源于32bit的黄金分割比
(注意XTEA/XXTEA也是这个常数)
解密脚本:
1 |
|
IDEA
52个子密钥是加密密钥对16bit加法和乘法(
子密钥应按照加密密钥相反的顺序使用。
解密代码略。自行搜索bouncycastle。
BlowFish
基于Feistel网络。
P数组(取Pi的小数部分):
243f6a88h,85a308d3h,13198a2eh,03707344h
解密代码略。
AES(Rijndael)
解密的模式有:
- ECB(Electronic Code Book,电子密码本)模式
- CBC(Cipher Block Chaining,加密块链)模式
- CTR(Counter,计数器)模式
- CFB(Cipher FeedBack Mode,加密反馈)模式
- OFB(Output FeedBack,输出反馈)模式
知道这些并没有什么用,到时候还是得一个一个试。
S盒:
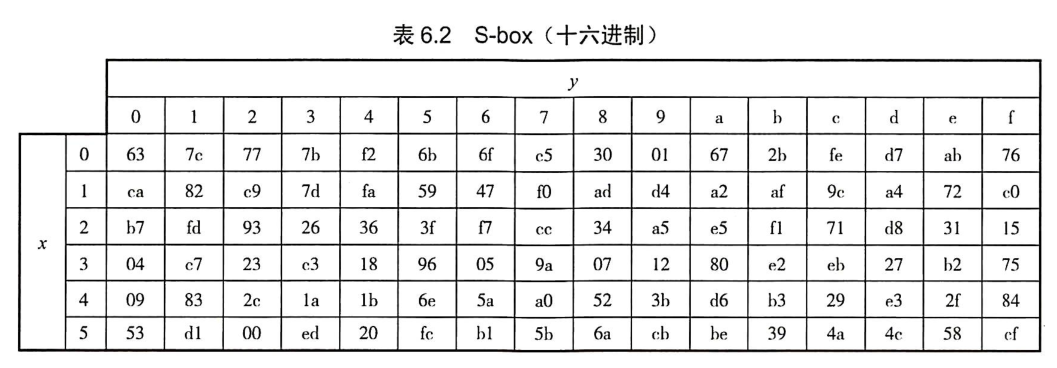
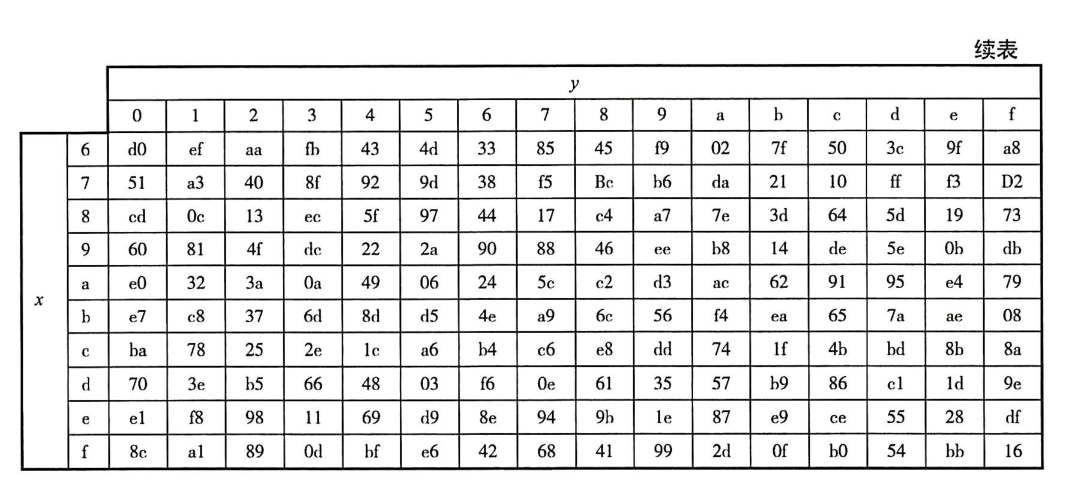
网上的解密网站都只能解自己的,解不了别人的。
解密网站:http://tool.chacuo.net/cryptaes
SM4
https://zhuanlan.zhihu.com/p/363900323
S盒:
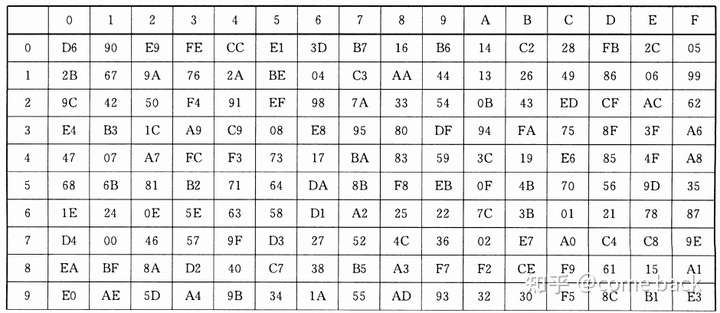
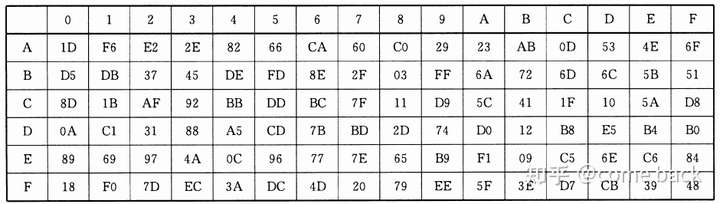
系统参数
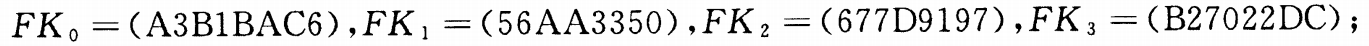
32个固定参数

解密工具见SM2处链接。
公钥加密算法——3/1/2022
RSA
- 公私钥的产生:
- 我们先随意选择两个质数
与 ,这里取 , ,计算 . - 根据欧拉函数
(小于或等于x的正整数中与x互质的数的数目),求得 . - 选一个小于r的整数
,使得 与 互质。并求得e关于r的逆元 ,即 。这里我们取 ,求得 - 销毁
与 .
- 我们先随意选择两个质数
由此,我们得到了公钥
加密信息:
假设B想给A传送信息
,他知道A产生的 与 。他使用先前约定好的格式(如Unicode,下有介绍)将 转换为一个小于 的正整数 ,使用下列公式将 加密为 : 不难计算,使用快速幂即可。 解密信息:
A得到B的消息后可以利用他的私钥
来解码,他使用下列公式将 还原成 。
关于对RSA攻击是密码学的专门内容,可以参考这篇文章。
ElGamal
- 密钥对生成:
- 取一个大素数
,随机数 与随机数 ,满足 且 . - 计算
. - 公钥为
, , ,私钥为 .
- 取一个大素数
- 加解密:
- 取随机数
,满足 ,且 . - 计算
. - 计算
, 即为密文. - 解密时计算
.
- 取随机数
- 签名:
- 取随机数
,满足 ,且 . - 计算
. - 设明文为
,找到满足 的解 .可证明满足条件的 唯一,签名即为 . - 验证签名时,需要满足
且 .
- 取随机数
对离散对数的攻击:BSGS、Pollard-Rho、Index-Calculus Algorithm、Pohlig-Hellman Algorithm等等。
如果用于不同明文加密的

DSA——3/2/2022
用于签名,不能用于加解密。
- 密钥对生成:
是 位长的素数. 且 , . 是 的素因子, . ,且有 . 为私钥, . . 、 、 、 为公钥. 为随机数, ,用后即丢弃.
- 签名生成:
- 输入明文
,公钥 、 、 ,私钥 ,随机数 . r = g**k % p % qs = inv(k) * (SHA-1(M) + x*r) % q,其中inv(k)是模 的乘法逆元. - 签名即为
.
- 输入明文
- 验证签名:
- 输入明文
,公钥 、 、 、 ,签名 、 . - 首先满足
且 . w=inv(s') % qu1=((SHA-1(M')) * w) % qu2=(r'w) % qv=(g**u1*y**u2) % p % q- 若
,则签名验证成功.
- 输入明文
ECC with GF(p)——3/3/2022
由于对数学知识要求较高,主要用于Crypto出题,在Re遇到的可能性较低,这里不给出具体原理.
算法原理 from wikipedia: https://en.wikipedia.org/wiki/Elliptic-curve_cryptography
算法原理 + py实现 from zhihu: https://zhuanlan.zhihu.com/p/101907402
可能有用的ECC模版:
1 | import collections |
SM2
SM2~SM4加解密工具:https://github.com/ASTARCHEN/snowland-smx-python
其它算法——3/1/2022
CRC32
只能用于校验文件,不能用来加密。
重点在于初始化生成的crctab表的识别。
算法就几行代码的事:
1 |
|
base64
因为比赛中可能会换表,甚至会修改算法的一些逻辑,因此了解一下其实现过程是很有必要的。
因为
对应方式很简单,就是列出3字节,24bit的01串(big endian)。然后每组6bit,分成四组。
每6个bit只能表示0~63这64个数,对应到base64的表(数组)中,替换成这64个字符。
为了保证转换后的串长是4的倍数,如果有6bit没有填充(注意这个跟值为0不同),就替换成=作为paddling。
举例如下图:
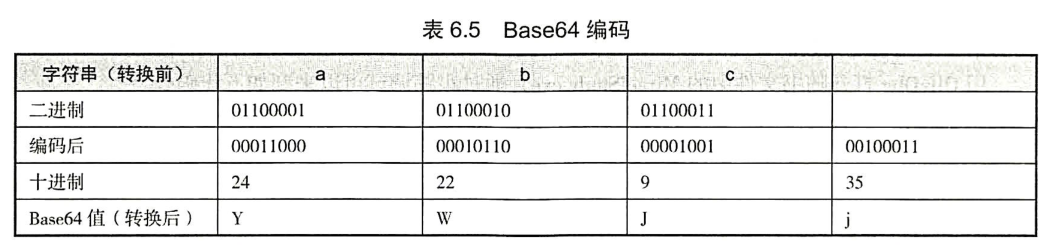
核心代码:
1 | for(i=0,j=0;i<len-2;j+=3,i+=4) |
常见加密库接口及其识别——3/3/2022
Miracl、FGInt、Crypto++、OpenSSL等等。
加密算法在软件保护中的应用——3/3/2022
许多软件证明安全和体验是矛盾的.
- 不要依赖自己设计的算法。
- 尽可能采用成熟的、安全性高的密码学算法。
- 定期更新密钥。
- 在成本允许的情况下,定期更新算法或安全机制。
- 严格按照标准建议的安全参数执行,使用标准化的安全算法或协议。
- 从攻击者的角度审视自己设计的安全机制。
- 在使用开源的密码箱算法库时,去掉对攻击者有用的信息提示。
- 时常关注密码学算法的最新进展。
Windows 内核基础
内核理论基础——1/4/2023
- 用户态程序的虚拟内存是互相隔离的,内核态程序共用一块虚拟内存,因此如果内核驱动写崩了就会蓝屏。
- 用户态程序无法访问内核态内存,反之可以。
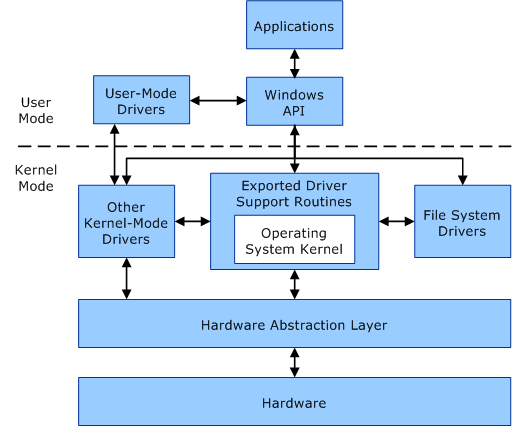
- 用户态的程序权限级别为 R3,内核驱动为 R0(最高)。
- 在 windows x64
中,用户态程序使用的虚拟内存范围为
0x000'00000000到0x7FFF'FFFFFFFF。0xffff800000000000之后为内核态。 - windows 驱动框架分为 NT 驱动、WDM 驱动与 KMDF 驱动。
- 每个驱动对象会创建一个或多个设备对象,每个设备对象会有一个指针指向下一个设备对象,形成一个设备链。
- windows 在称为设备树的树结构中整理设备,设备树中的节点称为“设备节点”,设备树的根节点称为“根设备节点”。通常根设备节点绘制在设备树的底部。
- 设备栈中的设备对象通过过滤设备对象(Filter DO)、函数设备对象(FDO)与物理设备对象(PDO)相连接。第一个设备对象位于设备栈的底部,最后一个创建的设备对象位于设备栈的顶部。
- R3 与 R0 通过 IRP 进行通信(联系网络通信的 packet),IRP 会沿着设备堆栈一路向下传递。
- IRQL 级别定义如下(数值越大级别越高):
1 |
|
有一个蓝屏错误代码就是
irql_not_less_or_equalThe IRQL_NOT_LESS_OR_EQUAL bug check has a value of 0x0000000A. This bug check indicates that Microsoft Windows or a kernel-mode driver accessed paged memory at an invalid address while at a raised interrupt request level (IRQL). The cause is typically a bad pointer or a pageability problem.
内核重要数据结构——1/5/2023
内核对象
常见的有 Dispatcher 对象、I/O 对象、进程对象与线程对象。
SSDT
https://www.ired.team/miscellaneous-reversing-forensics/windows-kernel-internals/glimpse-into-ssdt-in-windows-x64-kernel#finding-address-of-all-ssdt-routines
https://m0uk4.gitbook.io/notebooks/mouka/windowsinternal/ssdt-hook
System Service Dispatch Table or SSDT, simply is an array of addresses to kernel routines for 32 bit operating systems or an array of relative offsets to the same routines for 64 bit operating systems.
SSDT is the first member of the Service Descriptor Table kernel memory structure as shown below:
1 | typedef struct tagSERVICE_DESCRIPTOR_TABLE { |
In x64, the relation between SSDT and its function address is shown below:
FuncAddr = ([KeServiceDescriptortable+index*4]>>4 + KeServiceDescriptortable)
SSDT lookup:
1 | .foreach /ps 1 /pS 1 ( offset {dd /c 1 nt!KiServiceTable L poi(nt!KeServiceDescriptorTable+10)}){ r $t0 = ( offset >>> 4) + nt!KiServiceTable; .printf "%p - %y\n", $t0, $t0 } |
SSDT(shadow) struct:
1 | struct SSDTStruct |
Function Index to real function address:
readAddress = (ULONG_PTR)(ntTable[FunctionIndex] >> 4) + SSDT(Shadow)BaseAddress;
SSDT(shadow) lookup:
In x64 there is no symbols.
1 | 0: kd> !process 0 0 mspaint.exe |
TEB
TEB(Thread Environment Block,线程环境块)系统在此
TEB 中保存频繁使用的线程相关的数据。位于用户地址空间,在比 PEB
所在地址低的地方。进程中的每个线程都有自己的一个 TEB。一个进程的所有 TEB
都以堆栈的方式,存放在从0x7FFDE000开始的线性内存中,每 4KB
为一个完整的 TEB,不过该内存区域是向下扩展的。在用户模式下,当前线程的
TEB 位于独立的 4KB
段,可通过CPU的FS寄存器来访问该段,一般存储在FS:[0]。在用户态下
WinDbg 中可用命令$thread取得 TEB 地址。
FS:[000] 指向SEH链指针 FS:[004] 线程堆栈顶部 FS:[008] 线程堆栈底部 FS:[00C] SubSystemTib FS:[010] FiberData FS:[014] ArbitraryUserPointer FS:[018] 指向TEB自身 FS:[020] 进程PID FS:[024] 线程ID FS:[02C] 指向线程局部存储指针 FS:[030] PEB结构地址(进程结构) FS:[034] 上个错误号
1 | // Thread Environment Block (TEB) |
PEB
https://www.cnblogs.com/viwilla/p/5109966.html
内容已过时,目前Win10/Win11的PEB偏移已经变成了0x60。
PEB(Process Environment
Block,进程环境块)存放进程信息,每个进程都有自己的PEB信息。位于用户地址空间。在Win
2000下,进程环境块的地址对于每个进程来说是固定的,在0x7FFDF000处,这是用户地址空间,所以程序能够直接访问。
准确的 PEB
地址应从系统的EPROCESS结构的0x1b0偏移处获得,但由于EPROCESS在系统地址空间,访问这个结构需要有ring0的权限。
还可以通过TEB结构的偏移0x30处获得PEB的位置,FS段寄存器指向当前的TEB结构:
1 | mov eax, dword ptr fs:[0x30] |
或者通过TEB的指针获取:
1 | mov eax, dword ptr fs:[0x18] ;eax = *TEB |
在用户态下 WinDbg 中可用命令$proc取得 PEB 地址。
1 | //Process Environment Block |
内核调试基础——1/10/2023
见链接: http://blog.junyu33.me/2023/01/10/winkernel_environ.html